牵伸变换齿轮的齿数选配技巧

在设计牵伸变换齿轮时，应该了解牵伸倍数的变化范围Emin～Emax以及纱条重量的容许偏差δ。同时，希望以最少的变换齿轮数满足变换范围要求。

牵伸变换齿轮通常选择传动轮系中某一级的一个齿轮，或者一对相啮合的齿轮，必要时可变换两对相啮合齿轮，以求得最大的变换范围。

（一） 牵伸倍数数列和牵伸倍数变换级差率

牵伸倍数范围为E1，E2，E3，…，Ej，Ej+1，…，En，其中，E1为最小牵伸倍数，En为最大牵伸倍数，牵伸倍数有n 档。从Ej变换到Ej+1时，其牵伸倍数变换级差率为：

此级差率应满足纱条重量偏差δ 的要求，即：

牵伸倍数分档越细（n 越多），变换级差率ΔE 就越小，越易满足ΔE≤δ 的要求。但分档越多，变换齿轮的数量也就增多。理想的设计是：以最少的变换齿轮数量满足纺纱工艺对重量偏差的要求。

设只采用一个变换齿轮，若牵伸倍数的分布采用等差数列，变换齿轮的齿数之间只相差一齿，由ZA1～ZAm共m 档，对应的牵伸倍数为Emin～Emax＝CZA1～CZAm，此数列为等差数列，公差值为牵伸常数C，且有：

式中，E1是最小牵伸倍数。因此，各档变换级差率为：

由此可知，若变换齿轮的齿数为等差数列，则各档变换级差率不相等。第一档最大，随着齿数ZA的增大，级差率逐渐递减，变换齿轮的数量也过多。

若使每档牵伸倍数变换级差率相等，且小于偏差允许值δ，即：

则有：

这是一个等比数列，其公比φ 是相邻项的比值，任意项为Ej＝E1φj-1。

在相同牵伸变换范围内，等比数列比等差数列的档数要少得多，即变换齿轮数量也大为减少。故一般变换齿轮都按等比数列设计。

（二） 牵伸倍数等比数列公比φ 和变换总档数N 的确定

1.公比φ

在式（3-9）中，令ΔE≡k≤δ，可得：

由式（3-11）可根据纺纱工艺所要求的纱条重量偏差值δ 确定公比值φ。

2.变换总档数N

采用一对相啮合的变换齿轮（ZA，ZB），按递增公比φ 搭配而得牵伸倍数系列E1，E1φ，E1φ2，…，E1φn-1（其中E1为ZA＝ZB时的牵伸倍数），其指数公差为1，而En／E1＝φn-1，共有n 档。

若将ZA，ZB对调啮合，成为按递减公比φ-1 搭配，则可得牵伸倍数系列E1，E1φ-1，E1φ-2，…，E1φ-（n-1），其指数公差为-1，而En／E1＝φ-（n-1），也共有n 档。

以上两数列合并，去掉一个E1重复档，可得总档数为：

其中，最大牵伸倍数Emax＝E1φn-1，最小牵伸倍数Emin＝E1φ-（n-1），以B 代表Emax与Emin的比值，可得：

将式（3-12）代入式（3-13）可得变换档数：

因此，在B 和φ 确定后，即可由上式求得变换总档数N。

（三） 牵伸传动常数C

已知牵伸变化范围Emin～Emax，则可得：

故：

对牵伸传动机构来说，牵伸倍数的通式为：

式中：C 是牵伸传动常数，等于牵伸传动路线中除变换齿轮（ZA／ZB）以外各级齿轮速比和前后罗拉直径比的连乘积。由于齿轮齿数需为整数，设计时应尽可能使牵伸传动常数C接近工艺参数E1。

（四） 指数方阵表和变换齿轮数量的确定(www.xing528.com)

牵伸倍数数列按公比φ 等比数列设计，则按E＝C（ZA／ZB）可知，速比ZA／ZB的数列也应为同一公比φ 的等比数列。下面以四个齿轮为例，设Z1、Z2、Z3、Z4为四个变换齿轮的齿数，而且Z1＞Z2＞Z3＞Z4，可列出齿轮搭配的方阵表如表3-2 所示。

表3-2　齿轮搭配方阵表

设：

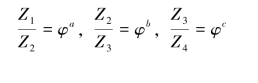
则：

将上述结果带入表3-2 可得表3-3。

表3-3　齿轮搭配比值方阵表

表3-3 可简化为以φ 的指数来表示，称为指数（x）方阵表，如表3-4 所示。

表3-4　齿轮搭配指数（x） 方阵表

由表3-4 可以看出，编制齿轮搭配指数方阵时可遵循如下规律。

（1）自左上至右下的对角线方格中全部指数值为零，即为一对变换齿轮齿数相等的情况。

（2）对角线左下方第一斜梯方格中的数值为级差指数，即相邻齿数比φx 中的指数值x。

（3）以对角线方格为分界，右上方对称方格内的指数绝对值与左下方相同，但为负值，故可从简不写，只写出对角线左下方的正数部分。

（4）对角线左下方除第一斜梯方格外，其他各格中的数值均可由该第一斜梯极差指数来确定。有三种确定方法：

① 该方格右侧数值与该方格所在竖列的第一斜梯极差指数之和；

② 该方格上方数值与该方格所在行的第一斜梯极差指数之和；

③ 从该方格所在的列和行所包含的全部极差指数之和。

所以，当已知第一斜梯方格的级差指数后，其他指数都可以由此求得。

（5）第一斜梯的级差指数应该选择适当，以保证全部指数能排成连续的整数数列，允许有重复，但不能有遗漏。如以4 只齿轮为例，可以写出表3-5 所示的两种方案，方案1 有缺档（4），故方案2 较理想。

表3-5　4 只齿轮的指数方阵表

表3-6 是满足牵伸倍数数列要求的相邻两齿轮齿数比φx 中指数x（即第一斜梯方格中的级差指数）的排列规律，可供设计者设计时查阅。

表3-6　变换齿轮只数、搭配档数及第一斜梯级差指数

续表

在设计时，根据所需的总档数N，查阅表3-6 中“不重复档数项”，即可确定齿轮的只数。同时可从表中查得相应的第一斜梯级差指数，即可进一步对各对变换齿轮的齿数进行确定计算。

（五） 变换齿轮齿数的确定

根据牵伸倍数等比数列有E＝E1φx；根据牵伸传动计算有E＝CZA／ZB。应分别使这两式中常数部分和变数部分基本互等，即：

式中：，为牵伸常数；C 为牵伸传动常数，由齿数比求得。

首先确定最小齿数，然后即可根据指数方阵表的最末一行来确定其他各齿轮的齿数。最大齿数则主要受有关机件可能容纳的空间尺寸所限制，应根据具体条件确定。应当指出：计算所得的变换齿轮齿数，都要按四舍五入的原则圆整为整数。

（六） 验算

圆整后的变换齿轮齿数需再要复核一下，确认是否满足以下纺纱工艺要求：是否满足牵伸倍数变化范围的要求；各档变换级差是否都能满足纱支重量偏差，即变换精度的要求。

若有个别档的变换级差率不能满足变换精度要求，则需要重新计算确定各变换齿轮的齿数。方法如下。

（1）增加最小齿轮的齿数，重新计算各个变换齿轮齿数，圆整后再进行上述验算，直至验算全部合格。

（2）选取更小的公比值φ。即增多变换齿轮数量m，然后根据m 可求得N，再重新修正φ 值。按照前述计算步骤重新计算确定变换齿轮数量和各变换齿轮的齿数，圆整后再进行上述验算，直至验算全部合格。

（3）个别调整。根据设计计算实践经验逐步完善之。