电压稳定约束下的无功优化模型考虑

1.电压稳定裕度指标

负荷节点电压与一个区域负荷或传输界面潮流之间的关系曲线如图8-4所示。图中A点为正常运行点，B点为临界运行点。通常，将两点之间的距离定义为电压稳定裕度，可用下式表示：

λ_VSM=（P^B-P^A）/P^A （8-6）

式中，P^A、P^B分别为正常运行状态和临界运行状态下指定区域所有负荷的有功功率之和。

电压稳定裕度的求取和以下因素相关：

1）当前电网运行状态和约束条件；

2）从当前正常运行状态向临界运行状态的过渡方式；

3）发电机的出力分配方式。

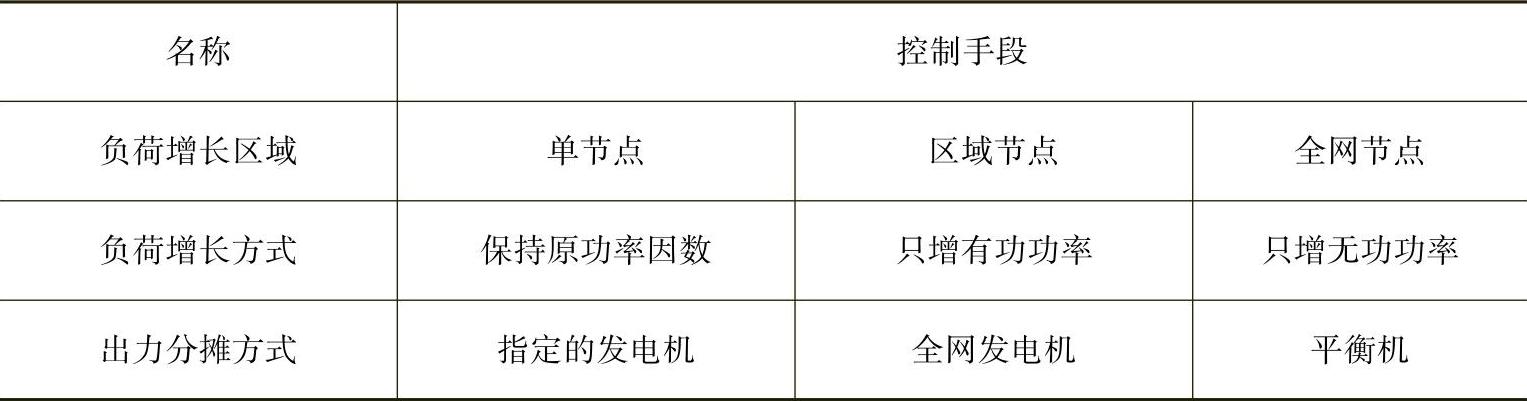
其中后两项需要事先设定，如表8-1所示。实际运用中，可采用不同组合，这些都以配置文件的形式读入。采用不同的设定方式可能会得到不同的电压稳定裕度。

图8-4 系统P-U曲线

表8-1 求取裕度的控制手段

2.目标函数

在保证一定电压稳定裕度的基础上以系统有功网损和控制成本最小为目标函数的模型如下：

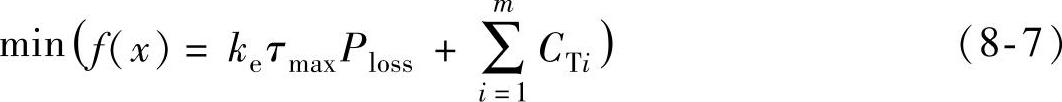
式中，k_e为单位电能费用，τ_max为全网的日最大负荷利用小时数，P_loss是系统有功网损，C_Ti为第i个控制手段的调节成本，m为可供调节的设备总数，x为状态变量，

x=[Q_g1，L，Q_gNG|Q_c1，L，Q_cNC|T₁，L，T_Nτ|λ_VSM||U₁，U₂，L，U_N|θ₁，θ₂，L，θ_N]（其中Q_g为发电机无功出力，Q_C为无功补偿容量，T为可调变压器档位，λ_VSM为电压稳定裕度，U为电压，θ为相位等状态变量。Q_C、T为离散变量，它们的处理往往是无功优化的难点。本书选用的是以二次罚函数的形式直接内嵌在内点法中。）

当电压稳定裕度不满足要求时，以增强电网电压稳定控制为主，来保证系统安全。(www.xing528.com)

3.等式约束条件

对于n节点系统，采用极坐标形式的电力潮流方程如下：

式中，i=1，2，…，n；j为与节点i相连的节点集合。

4.不等式约束条件

传统的无功优化模型的不等式约束条件依次为节点电压上下限、节点无功上下限、变压器电压比的上下限、发电机机端电压的上下限，即

本书采用加入电压稳定裕度和无功储备约束的模型。

电压稳定裕度约束可用如下广义参数潮流方程表示：

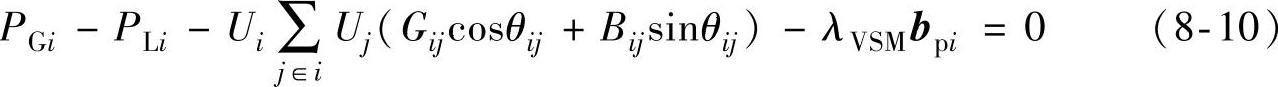
上式即为常规电力潮流方程和电压稳定裕度参数化标量λ_VSM和b_pi的组合，b_pi=[b_p1，…b_pm]^T是方向矢量，表示负荷增长的方向，求取裕度时需要增加某一节点区域的负荷，则b_pi中相应元素不为零。

为使系统安全，要有一定的电压稳定裕度，即要满足λ_VSM≥λ^S_VSM，λ^S_VSM为电压稳定裕度的基值。

5.发电机无功储备约束

为适应事故后电网电压保持一定水平的要求，发电机要有一定的无功功率储备，定义无功功率储备率表示如下：

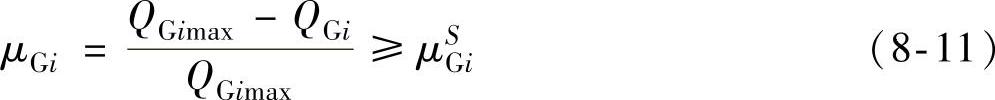
式中，Q_Gi为第i台发电机正常运行时的无功出力；Q_Gimax为第i台发电机的无功出力上限；μ^S_Gi为第i台发电机无功储备的基值。

模型的求解方法众多，有内点法、遗传算法等，本书不再赘述。