电压稳定裕度的计算方法

正常运行状态的电压稳定分析：给出当前运行状态的电压稳定薄弱环节、各节点电压与负荷水平的灵敏度、电压稳定裕度等信息，能考虑各种负荷增长方式、各种运行/控制约束。电压稳定分析算法应包括连续潮流法等，保证预想故障集扫描的精确度、速度及可靠性。

预想故障的自动扫描：找到影响系统电压稳定性的关键故障，应能自动生成电网元件的N-1预想故障集，包括线路、主变压器和发电机元件的N-1开断，并可自定义重要的预想故障集。对严重的故障可进行重点分析。

除进行全网负荷增长模式下的在线电压稳定分析外，还可对500kV变电站供电区负荷增长模式进行在线电压稳定分析，并可在500kV主变压器中压侧增加虚拟的无功负荷，计算各500kV变电站的无功储备裕度，并使计算结果按严重程度排序。

3.6.1.1 连续潮流法

连续潮流方法（Continuation Method，又称延拓法）是跟踪非线性动态系统平衡点解轨迹的一种基本方法。描述电力系统的参数化动态方程组为

式中，x是系统静态状态向量，即节点电压幅值和相角；y是系统动态状态向量，如发电机内电势和转子角等；λ是一个反映系统负荷水平的标量参数；g包括发电机和负荷等元件的动态方程，f是节点潮流平衡方程。系统的平衡点方程为

非线性方程组式（3-43）的未知变量的个数比方程个数多1个，用连续法可以得到平衡点解轨迹。采用不同的测试函数，可以得到不同类型的分岔点：鞍结型分岔点、约束诱导型分岔点、霍普夫分岔点或奇异诱导型分岔点等。系统的动态雅可比矩阵为

在满足下面四个前提条件下，标准潮流方程的雅可比矩阵的奇异性等价于动态系统雅可比矩阵J_dyn的奇异性。

1）发电机自动电压调整的静态电压差为零；

2）由于松弛发电机的负荷频率响应，系统静态频率差为零；

3）发电机机械和定子损耗忽略不计；

4）负荷的有功、无功功率不依赖于电压。

这是潮流方程雅可比矩阵奇异性用于分析系统静态稳定性的理论基础。电力系统参数化的潮流方程可写为

f（x，λ）=0 （3-45）

连续潮流（Continuation Power Flow，CPF）已经成为在电力系统静态稳定性分析中的一个基本分析工具。应用于连续潮流问题中的连续方法主要有同伦连续方法和预测校正连续方法两类。较早被用来进行静态稳定极限点计算的是同伦连续方法，而真正实用的是预测校正连续方法。

3.6.1.1.1 预测环节

所谓预测环节就是根据当前点及其以往几点来给出解轨迹上下一个点的估计值，从而有利于下一点求解的快速收敛。连续潮流中通常采用的预测方法有一阶微分方法（如正切预测法）和多项式外插方法（如二分法等）。在计算量上，多项式外插方法要少于一阶微分方法，但是前者的应用要更为广泛。这主要是因为在计算过程中通常要检查是否已经穿越分岔点，而这通常要通过计算一阶微分来判断。此外，虽然预测过程中计算一阶微分的扩展矩阵可以与校正过程中参数化后的扩展矩阵不同，但是采用相一致的扩展矩阵是一个常见的选择。因为这会使得在预测过程中不必对扩展矩阵进行因子化的工作，而仅仅是一次快速前代和一次完全回代的计算量。变量和参数的预测值可写为

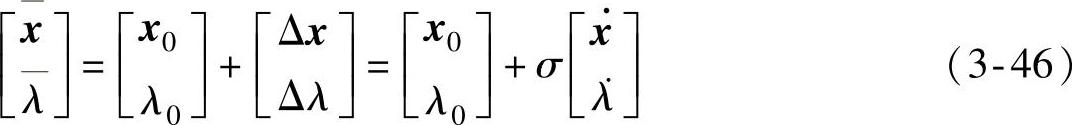
式中，x₀和λ₀为当前点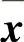；和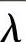为下一点的估计值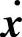；和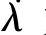为当前点的梯度；σ为步长。

3.6.1.1.2 校正环节

校正环节就是以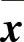和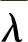为初始点计算得到实际满足潮流方程的运行点x₁和λ₁。通常采用的校正方法有牛顿法和拟牛顿法等。

3.6.1.1.3 参数化策略

参数化策略是贯穿整个连续方法的核心，它决定了整个连续潮流应用的面貌。通常采用的参数化方法有局部参数化方法、弧长参数化方法、拟弧长参数化方法和正交参数化方法等。

连续潮流基本方程如下：

f（x）+λb=0 （3-47）

式中，x∈Rⁿ；f（x）为n维函数矢量；b为负荷增长方向，b∈Rⁿ；λ为实参变量，从物理的角度说，它实际上在一定程度上代表着系统的负荷水平。

上述的连续潮流基本方程有n+1个变量，但只有n个方程，是不能求出定值解的。它实际上是n+1维空间上的一条曲线。为求得定值解，必需增加一个方程。

最简单也最直观的方法就是在每次计算中先确定λ值，而后采用常规的潮流计算方法即可求得对应的定值解。但当λ取某一较大值时，潮流雅可比矩阵可能出现病态，且随着λ值的继续增大，其病态性将更趋严重，当λ大到一定程度时，潮流雅可比矩阵的病态将使得常规潮流计算无法收敛。图3-12所示的逐点计算法说明图直观地说明了这一点。随着负荷水平的加重，λ值不断增加，预测点x_p向右移动，当x_px与λ-V曲线相切时，x即为电压崩溃临界点，但由于雅可比矩阵在临界点处奇异，临界点附近病态，潮流计算将无法收敛，数值计算失败。为克服该缺点，弧长连续潮流法便应运而生。

图3-13直观地给出了弧长连续法的基本概念。其基本思路是通过引入参数S代表从x到初始点x₀的弧长，并取S等于x₀x_p的长度来实现，即

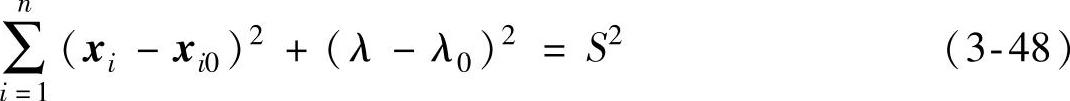
式中，。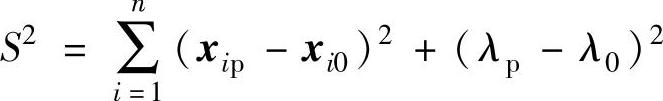

图3-14直观地给出了同伦连续法的基本概念，其基本思路是令矢量x-x_p与矢量x₀-x_p垂直，由此可增加方程

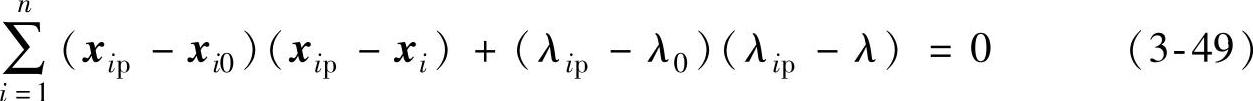(www.xing528.com)

图3-15直观地说明了局部参数连续法的基本概念。其基本思路则是根据预测方向先确定矢量x的某一元素，即根据x₀及x_p增加方程：

x_k=x_pk （3-50）

式中，k为局部连续化参数对应的下标，实用中一般取矢量x_p-x₀绝对值最大元素对应的下标，对于连续潮流计算，则可将k限定于电压所对应的元素。

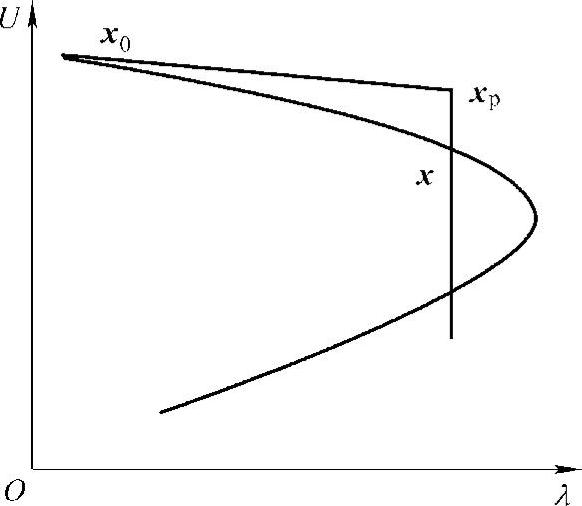
图3-12 逐点计算法说明图

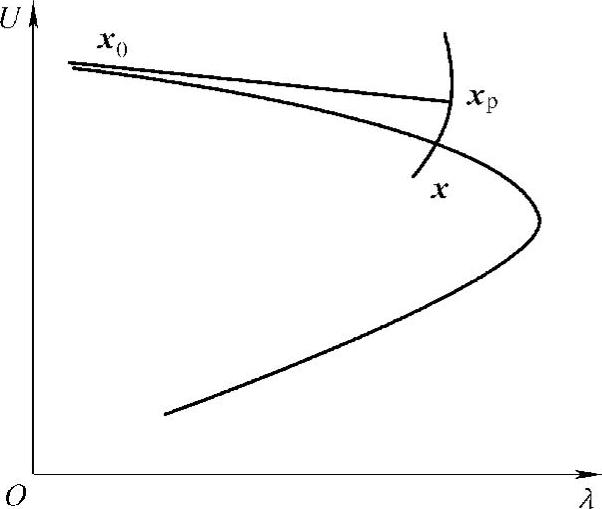
图3-13 弧长连续法说明图

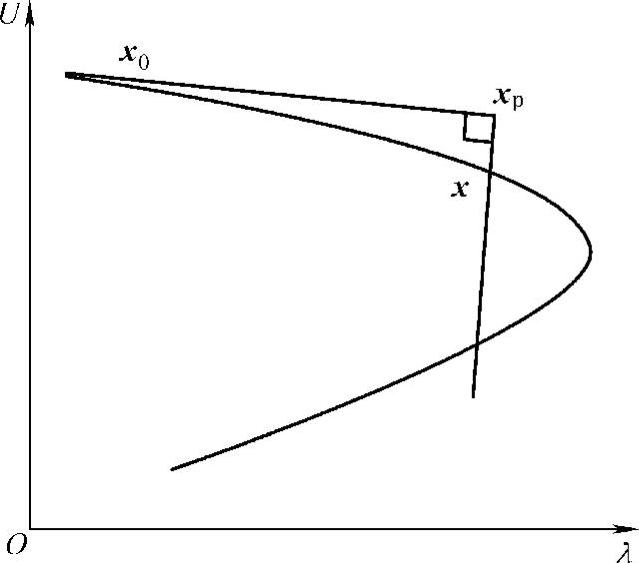
图3-14 同伦连续法说明图

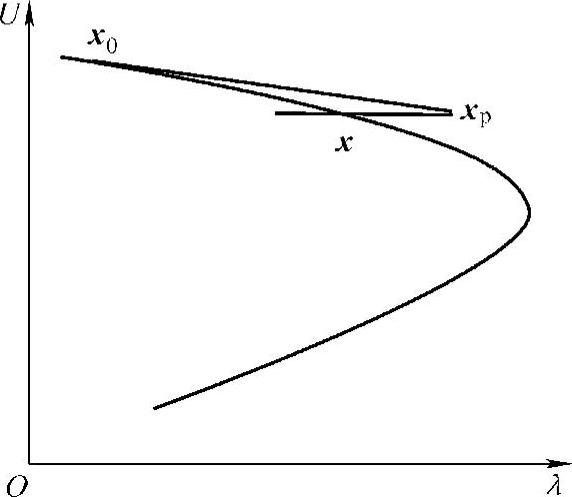
图3-15 局部参数连续法说明图

经过上述处理，扩展潮流方程有n+1个方程和n+1个变量，由此即可求得定值解。从空间解析几何的角度来看，连续潮流计算的每一点相当于求λ-V曲线与新增方程所对应的空间曲面的交点。用牛顿-拉夫逊法迭代求解多维空间中一条曲线与一个曲面的交点，当该曲线与曲面相切时，对应的雅可比矩阵奇异，数值计算将无法收敛，正交时其收敛性则应最好，相交时其收敛性介于两者之间。潮流方程雅可比矩阵临界点处的奇异来源于λ-V曲线与λ恒定曲面的相切。对于连续潮流法，由于新增方程对应的空间曲面与λ-V曲线不再相切而是相交，从而使得扩展的潮流雅可比矩阵不再奇异。

为说明方便，将以上增加的方程统一用g（x，λ）=0表示。用牛顿-拉夫逊法解扩展潮流方程，则相应的修正方程如下：

式中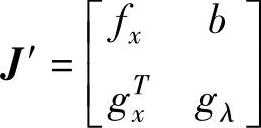，，J=f_x为常规潮流的雅可比矩阵，上标T表示转置。

上式的扩展潮流方程的雅可比矩阵J′即使在临界点处也是非奇异的。若扩展雅可比矩阵三角分解时选主元，修正方程的计算精度可以得到有效保证，连续潮流计算的收敛性可以得到有效保证，但其计算量较大，在实用中一般是难以接受的。若扩展雅可比矩阵三角分解时不选主元，由于其左上角部分矩阵即为潮流雅可比矩阵，而它在临界点处却是奇异的，故在临界点附近修正方程的计算精度可能较低，并可能进一步影响连续潮流计算的收敛性。

为克服上述缺点，这里对局部参数连续法的算法实现进行适当修改。在迭代求解λ-V曲线与新增方程x_k=x_pk的交点的过程中，不将x_k=x_pk当作方程来考虑，而是将x_k当作常量，并将方程f_k（x）+λb_k=0移至最后一行。相应的采用牛顿-拉夫逊法迭代求解所对应的修正方程如下：

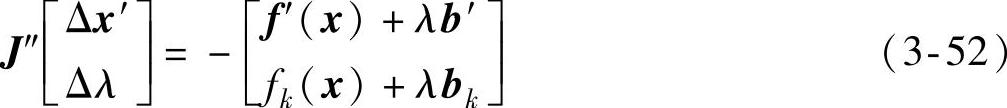
式中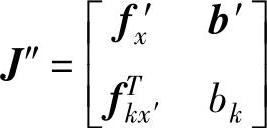，；f_x′为f_x划去第k行第k列后的矩阵；b′为矢量b划去第k个元素后的矢量；b_k为矢量b的第k个元素；x′为矢量x划去第k个元素后的矢量；f′（x）为矢量函数f（x）划去第k个元素后的矢量；f_k（x）为矢量函数f（x）的第k个元素；f_kx′为函数f_k（x）对x′的梯度矢量。

可以看出，J″事实上是J′划去第n+1行第k列后将第k行移到最后一行而得到的。

对于局部参数连续法，g_x^T=（0，…，0，1，0，…，0）（k维），g_λ=0。现假设J″在临界点处奇异，则∃w=（w₁，w₂，…，w_n）T≠0，使得J″w=0。构造矢量w′=（w₁，w₂，…，w_k-1，0，wk，…，w_n）T，则有J′w′=0。由w≠0可得w′≠0，故有J′奇异。这与正常拐点处J′非奇异矛盾，此即证明了若临界点为正常拐点，J″在临界点处非奇异。

对于电力系统连续潮流计算，在电压崩溃临界点及其附近，按照上述下标k的选择原则，x_k应该对应于电压下降最快节点的电压，这表明f_x′是将系统最薄弱节点当作PU节点处理时的潮流雅可比矩阵。从物理的角度看，将某一节点当作PU节点处理实际上意味着该节点电压维持恒定。可以想象，如果在系统的某一薄弱节点投入充足的无功电源以维持该节点电压恒定，则系统的电压稳定裕度必将增大，这就意味着f_x′临界点处非奇异。由此可见，即使在临界点处，f_x′及J″均非奇异，连续潮流法能够可靠地计算到电压崩溃临界点。

经过上述改进，连续潮流法较好地克服了潮流雅可比矩阵临界点处奇异及其附近病态给数值计算带来的不良影响，并保持了较好的稀疏性，能够可靠地计算到电压崩溃临界点及λ-V曲线的下半分支，并保持较好的收敛性和较快的计算速度。

3.6.1.1.4 步长控制策略

步长控制策略的选取是决定连续潮流有效性的一个关键问题。步长太小或太大都不是好的策略。前者将造成计算点数太多，后者将使得校正过程收敛缓慢，甚至发散而不得不收缩步长从新计算。步长控制策略中的参数在很大程度上要根据具体系统情况来决定。在对电力系统的计算，经过大量试算调试得到了一组最优的步长控制参数。采用该组参数，使得每个连续潮流计算大致由7～12个解点构成，这是该方法满足在线应用的关键之一。

3.6.1.2 非线性规划法

非线性规划法首先将临界点的求取转化为负荷最大化问题，而后采用非线性规划的方法进行求解。

在极坐标系统中，电压稳定临界点的非线性规划模型可描述如下：

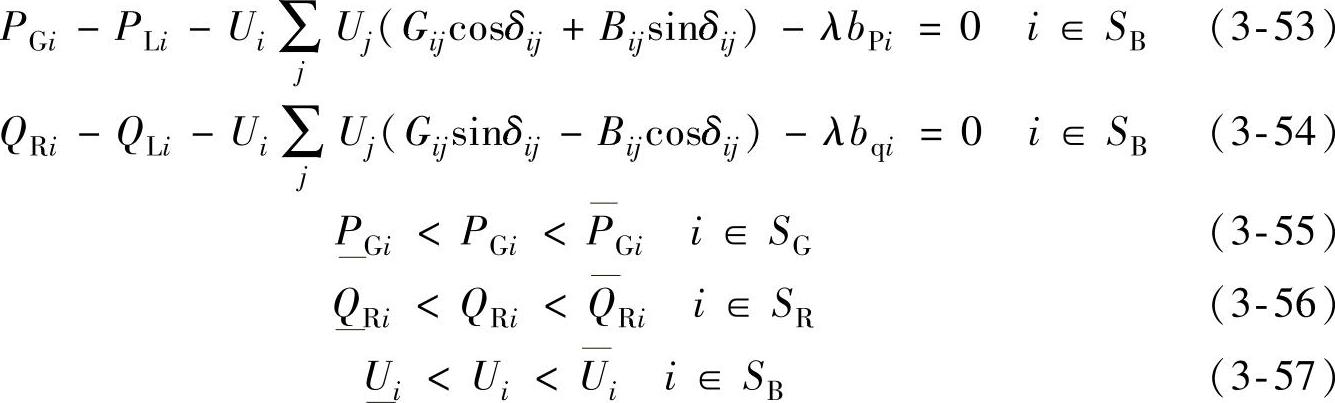
式中，S_B为所有节点的集合；S_G为有功电源集；S_R为无功电源集。

基于非线性规划的临界点问题具有大量的不等式约束条件，不等式约束的处理是影响算法成败的关键。

3.6.1.3 预想故障集扫描计算的新方法

电网在线电压稳定监视与控制提供对预想故障集（N-x：x≥1）进行扫描的功能，既能提供当前运行状态下的裕度指标，也能提供各预想故障条件下的裕度指标，还能根据扫描结果对预想故障进行排序，确定对电压稳定有较大影响的严重故障方式，并进行故障前后的静态电压稳定水平比较。

由于预想故障集的规模一般较大，电压稳定裕度指标计算的性能是预想故障集扫描能否在线应用的关键。连续潮流法原理简单，能给出准确的λ-U曲线等信息，收敛可靠性高，但计算量一般较大，且依赖于预想故障后初始潮流计算的收敛性；非线性规划法可直接计算电压崩溃临界点，而无需计算λ-U曲线，也无需计算预想故障后的初始潮流，计算量相对于连续潮流法一般要小得多，但算法的收敛可靠性低于连续潮流法。为充分利用连续潮流法与非线性规划法的优点，可采用以非线性规划法为主，连续潮流法为辅的方法进行预想故障集扫描，即先采用非线性规划法进行电压稳定分析，若非线性规划法不收敛则启用连续潮流法进行电压稳定分析。由于非线性规划法本身的收敛可靠性还是比较高的，启动连续潮流计算的概率较低，算法的计算量总体上与单纯采用非线性规划法时的计算量相差不大。由于连续潮流法和非线性规划法的收敛性互不相关，且各有自己适用的场合，综合采用两种算法的收敛可靠性明显高于单独采用非线性规划法或连续潮流法的场合。