无功优化的基本概念和作用

1.无功优化的定义及数学模型

电力系统无功优化，是指当系统有功负荷、电源、潮流及网络结构给定的情况下，通过优化计算确定系统中某些控制变量的值，以找到在满足所有约束条件的前提下，使系统的某一个或多个性能指标达到最优时的运行方式。其需要研究的就是在满足系统负荷需求及运行约束要求的条件下，使电网的某一个或多个指标达到最优的无功功率分布方案。

根据所研究问题的时间跨度长短，无功优化可以分为无功规划优化和无功运行优化。其中，电力系统无功规划优化主要以今后5～10年的电网规划为依据，在保证满足各种典型方式安全约束的前提下，确定最优无功补偿地点、类型和容量，从而达到经济效益最好的目的。电力系统无功运行优化主要是以当前电网运行状况为依据，在满足各种安全约束的前提下，确定最优无功补偿地点、类型和容量，保证电网电压制量，减少线路功率损耗，从而达到经济效益最大的目的。

由于电力系统规模大，有多种运行方式，负荷变化具有地域性、随机性，加上无功/电压控制设备种类繁多，性能差异较大，响应速度有快有慢，有的可以连续控制，有的只能离散控制，因而无功优化一直是电力系统领域的重点和难点问题之一。随着高压远距离输电技术的实现，各区域电网互联，组成统一整体，使电网能在更大范围内实现无功补偿调节、错峰、调峰等功能，从而在更大的空间内合理分配电力资源。随着厂网分开、竞价上网的电力市场改革的进行，研究互联电力系统无功分布是否合理，以及如何对无功/电压控制设备进行统一调度而实现电网的整体最优效益，不仅影响到整个系统的供电质量和经济效益，更关系到系统能否安全稳定运行。

电力系统无功优化在数学上可以表示为

min f（x）

约束 h（x）=0 （1-1）

式中，矢量x包括：控制变量和状态变量，如节点电压幅值、相角、无功补偿设备补偿容量、有载调压变压器档位等；f（x）为系统的目标函数；h（x）为等式约束，即潮流方程约束；g（x）为不等式约束。

由上式可见，电力系统无功优化问题的数学模型包括功率约束方程、变量约束和目标函数等。

（1）目标函数

无功优化的目标函数因侧重点不同而具有多样性，包括从经济性角度出发的系统有功网损最小；从安全性角度出发的、采取系统节点电压幅值偏离期望值的二次方和最小或者电压稳定裕度最大为目标函数；综合经济性和安全性考虑的，在保证最优电压质量前提下的有功网损最小；考虑增大系统的无功备用容量、减少网络损耗以及减小电压偏移的多目标无功优化；涉及网损、设备操作费用和动作设备数量的实时多目标无功优化；考虑电压稳定的无功优化等。

（2）潮流平衡方程(https://www.xing528.com)

在无功优化模型中，系统每一节点的注入有功功率和无功功率都应满足下式：

式中，P_i和Q_i分别为节点i的注入有功功率和注入无功功率；U_i和U_j分别为节点i和节点j的电压幅值；B_ij为节点i和节点j之间的互电纳；N_B为总节点数；G_ij为节点i和节点j之间的互电导；δ_ij为节点i和节点j之间的相角差。

（3）变量约束条件

电力系统在稳态运行时，为了保证电力系统运行的安全和电能质量，各节点的电压幅值必须维持在额定电压幅值附近。同时，发电机有功功率、无功功率输出均有一定的限制，这些限制便构成了电网的运行约束条件。而调整发电机机端电压、变压器分接头位置和无功补偿电源输出，都受到运行条件和设备本身条件的限制，这些限制便构成了控制变量约束。

一般选取发电机端电压U_G、无功补偿容量Q_C、可调压变压器分接头位置T_K为控制变量，而发电机无功功率Q_G、负荷节点电压U_D作为状态变量。

控制变量的不等式约束为

式中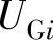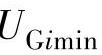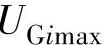，，，分别为发电机节点i的端电压及其下限值和上限值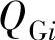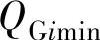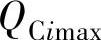；，，分别为节点i的无功补偿容量及其下限值和上限值；T_K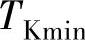，，分别为可调压变压器分接开关位置及其下限值和上限值；N_G，N_C，N_T分别为电网中发电机节点数，无功补偿节点数，可调压变压器台数的集合。

状态变量的不等式约束为

式中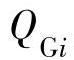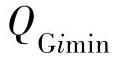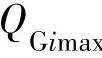，，，分别为发电机节点i的无功功率及其下限值和上限值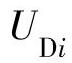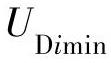；，，分别为负荷节点i的电压及其下限值和上限值；N_G，N_PQ分别为系统中发电机节点集合和PQ节点集合。

2.无功优化特点

电力系统无功优化是一个多变量、多约束的混合非线性规划问题，其控制变量既有连续变量又有离散变量。同时无功优化可能是一个多峰多极值问题，而不能保证其是一个单峰函数，初值选取不当可能会导致问题收敛到局部最优点，并且现代电网包含众多的节点和出线，越是电压等级低的网络，其节点数往往越多，网络越复杂。无功优化问题的突出点有：多目标性，约束条件数量多、类型多，目标函数及约束条件的非线性，控制变量的离散性，负荷及运行方式的不确定性，非凸性和多极值性，大规模，目标函数难以由控制变量表示描述等。