1.管路特性方程
图8-32所示为一台水泵与一条管路相连接的排水管路系统。若以H表示水泵给水提供的压头，取吸水井面1-1为基准面，列1-1面和排水管出口截面2-2的伯努利方程，则
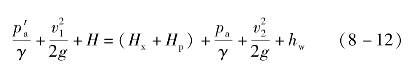
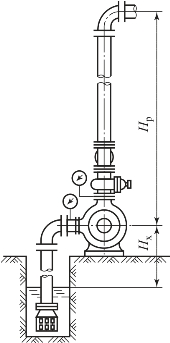
图8-32 排水设备示意图
式中 p′a，pa——分别为1-1和2-2截面上的大气压，矿井条件下，两者相差很小，可认为相等；
Hx，Hp——分别为吸水高度和排水高度，两者之和为测地高度或实际扬程Hsy，即Hsy=Hx+Hp，m；
v1——吸水井液面流速，由于吸水井与水仓相通且液面较大，水流速度很小，可认为v1=0，m/s；
v2——排水管出口处的水流速度，即排水管的流速vp，v2=vp，m/s；
hw——管路系统的水头损失，它等于吸水管水头损失hx和排水管水头损失hp之和，m。
即
由流体力学得
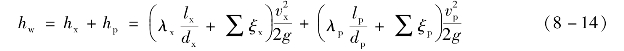(www.xing528.com)
式中 vx——吸水管路的流速，m/s；
λx，λp——吸、排水管路的沿程阻力系数；
∑ξx，∑ξp——吸、排水管路的局部阻力系数之和；
lx，lp——吸、排水管路的实际管路长度，m；
dx，dp——吸、排水管路的内径，m。
将式（8-13）代入式（8-12），整理后得
式（8-15）称为排水管路特性方程式。该式表达了通过管路的流量与管路所消耗的压头之间的关系。式中的R为管路阻力系数，其计算式为
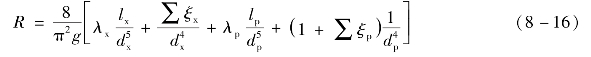
对于具体的管路系统而言，其实际扬程Hsy是确定的，因而当管路中流过的流量一定时，所需要的压头取决于管路阻力系数R，即取决于管路长度、管径、管内壁粗糙度及管路附件的形式和数量。
2.管路特性曲线
将式（8-14）中Q与H的对应关系绘制在Q-H坐标图上，则得到一条顶点在（0，Hsy）处的二次抛物线，即排水管路特性曲线，如图8-33所示。
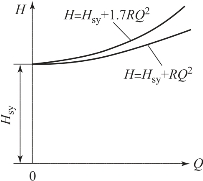
图8-33 管路阻力特性曲线
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
