伪随机序列的实例展示

1.m序列

m序列是最长线性移位寄存器序列的简称。它是由多级移位寄存器或其他延迟元件通过线性反馈产生的最长的码序列。由于m序列容易产生、具有很好的规律性和相关性能，在扩频通信中最早获得广泛的应用。

（1）m序列的自相关性

m序列的自相关函数具有双值特性，如图4-3所示。自相关函数满足

图4-3 m序列的自相关函数曲线

（2）m序列的互相关性

移位寄存器的结构不同，产生的随机码序列的周期长度也不一定相同，即使周期相同，两两m序列对的互相关特性差别也很大，有的m序列对的互相关特性好，有的则较差，甚至不能实际使用。一般说来，随着序列周期的增加，其互相关值的最大值会递减。在实际应用中，设计者只关心互相关特性好的m序列对的特性和数量。

通常互相关特性好的m序列对称为优选对，它是指在m序列集中，其互相关函数最大值的绝对值小于某个值的两个m序列。我们设计m序列的目标就是在互相关特性满足系统要求的条件下，使得优选对尽可能多，以便产生更多的扩频码供用户使用。

m序列具有移位相加性，移位相加性是一个m序列M_p与其经任意延迟移位产生的另一不同序列M_r模2相加，得到的仍是M_p的某次延迟移位序列M_s，即M_p⊕M_r=M_s。1100101与向右移三位后的序列1011100逐位模二相加后的序列为0111001，相当于原序列向右移两位后的序列，仍是m序列。

2.Gold码序列

Gold码是m序列的复合码，是由R.Gold在1967年提出的。如果把两个m序列发生器产生的优选对序列模2相加，则产生一个新的码序列，即Gold序列。这种序列有较优良的自相关和互相关特性，Gold码的互相关函数的旁瓣的极大值不超过该m序列互相关函数的最大值。所以Gold码序列的互相关特性优于m序列，但是Gold码序列的自相关性不如m序列。Gold序列的序列数远多于m序列，因而获得了广泛的应用。

3.M序列

M序列是最长序列，它是由非线性反馈逻辑和移位寄存器构成的序列发生器所能产生最大长度序列。M序列的长度已达到n级移位寄存器所能产生的序列的最长周期2ⁿ，所以又称为全长序列。M序列的构造可以在m序列的基础上实现。

M序列不再具有移位相加性，因而其自相关函数不再具有双值特性，而是一个多值函数。

4.沃尔什（Walsh）码序列

沃尔什序列是完备的正交函数集，具有理想的互相关特性，即两两之间的互相关函数为“0”，即它们之间是正交的。沃尔什码序列产生的规则如图4-4所示。

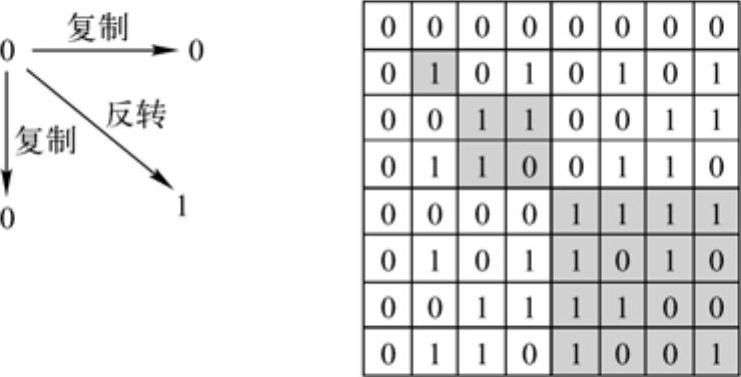
图4-4 沃尔什码的生成示意图

在图4-4中，根据生成规则，分别进行复制和反转就得到一个沃尔什码的矩阵，其中灰色表示反转之后取得的结果。图4-4是一个8维的沃尔什码，被标识为。其中8表示8维，表示第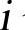个沃尔什码。(www.xing528.com)

沃尔什函数的性质如下：

1）正交性。例如在图4-4中，第4个沃尔什码与第8个沃尔什码进行模2加，01100110⊕01101001=00001111，结果中有4个“1”，4个“0”，完全正交。

2）两个沃尔什函数相乘的结果仍为一个沃尔什函数，这一性质表示沃尔什函数对于乘法是自闭的。

3）沃尔什函数集是完备的，即长度为N的沃尔什序列共有N个。

4）沃尔什函数在同步时是完全正交的，但在不同步时，其自相关和互相关特性均不理想，并随同步误差值增大而快速恶化。

正是由于上述特性：沃尔什函数通常用于易实现同步的下行链路中，区分同一用户不同逻辑信道。

5.正交可变速率扩频增益（OVSF）码

OVSF码是Walsh函数的一种，在WCDMA中用作信道化码。移动通信已由单一速率的语音拓展为不同速率的语音、数据与图像的多媒体业务，在扩频过程中，不同的速率业务要采用不同的扩频比，才能达到同一信道传送的码片速率。同时，由于在同一小区中，多个移动用户可以同时发送不同的多媒体业务，为了防止多个用户不同业务之间的干扰，需要一种可满足不同速率业务和不同扩频比的正交码，OVSF码是其中一种。

（1）OVSF码的自相关特性

将两个相同的OVSF码按位模2加后运算结果为0，其运算结果如图4-5所示。在此处采取的是负逻辑，即数字“0”对应于电平+1，数字“1”对应于电平−1，按位求和结果为“8”。8个“0”对应于电路实现的8个高电平，累加后归一化的结果为1，推广的结论为

图4-5 OVSF码的自相关特性

（2）OVSF码的互相关特性

同阶的两个不同OVSF码的互相关特性如图4-6所示。两个不同的OVSF码按位求和结果为“0”。此时，称这两个OVSF码是正交的。推广的结论为

综合上述（1）和（2）两种情况，OVSF码的正交特性总结如下：

在同步状态下，对同长度的OVSF序列码组来说，两个相同的OVSF序列码的模2加之和的归一化值等于1，两个不同的OVSF序列码是正交的，模2加之和的归一化值等于0。

图4-6 OVSF码的互相关特性