松过程经验似然方法的性能评估：广泛的仿真研究

为了评估所提出的经验似然方法的性能，我们进行了广泛的仿真研究.首先，从伯努利（p＝0.5）和U（τ/2，τ）生成协变量Zi（t）和后续时间Ci.

我们假定Oi（t）是泊松过程，其中λ0（t）＝c/τ，c是常数.然后给定Zi，观察数服从泊松和观测时间来自U（0，Ci）中大小为的随机样本的次序统计量.为了生成面板计数数据Yi（Ti，j），我们假设

其中Ti，0＝0.给定Zi（t）和Fit，我们假设和遵循泊松分布且均值函数分别为

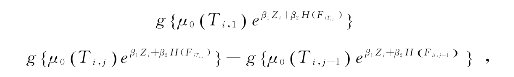
i＝1，...，n，j＝1，....

在所有情况下，我们取W（t）＝1，c＝5，γ＝1，和H（Fit）＝Oi（t-）.我们为真实值β选择四种不同的设置β＝（β1，β2）：（0.1，0.1），（0.3，0），（0，0.1），（0.3，0.1），且考虑的样本大小n＝30，50，70.由{g（t）＝t，μ0（t）＝t}，{g（t）＝log（t），μ0（t）＝t}和{g（t）＝t2，μ0（t）＝exp（t）}的计算得出根据模拟结果并且分别对应表6.1，表6.2，表6.3，模拟结果内容有关β＝（β1，β2）的置信区间的覆盖率（CP）和平均长度（AL）.还考虑了μ0（t）的两个不同设置.所有模拟结果均基于2000次重复.

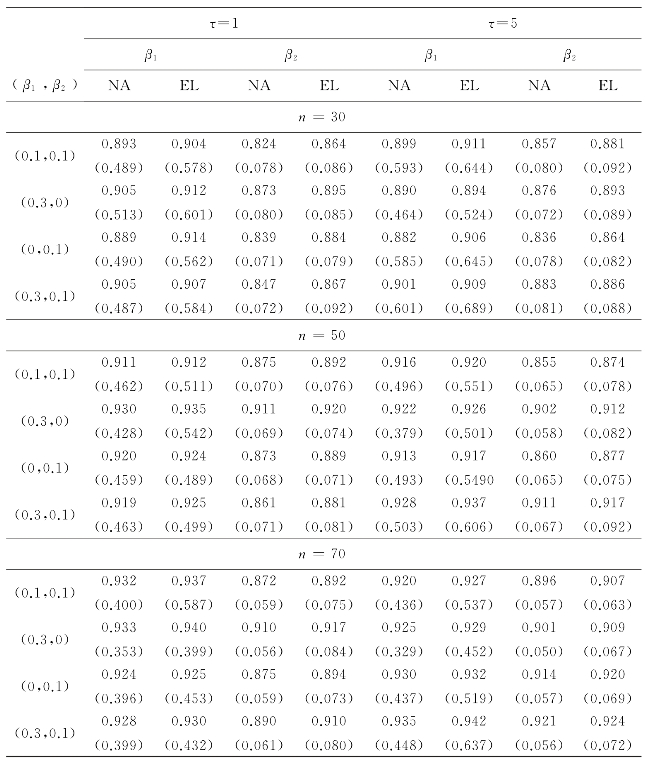
从表6.1中我们可以看到，在几乎所有情况下，经验似然法在置信域的覆盖概率方面都优于普通近似法.当样本量较小时，结果特别值得注意.经验似然方法在不同参数设置下保持稳定.并且，随着样本量的增加，覆盖率越来越接近名义水平0.95.值得注意的是，对于经验似然法，我们以更大的平均长度为代价获得了更好的覆盖率.我们在表6.2和表6.3中获得了相似的结果.(www.xing528.com)

对于较大样本量的正态逼近和经验似然，结果相似.同样，经验似然法在计算上也很昂贵.对于高维数据，计算将变得非常耗时.考虑到这些，当样本量相对较小时，人们可能更倾向于采用经验似然法.

表6.1　在g（t）＝t，μ0（t）＝t下，置信水平为0.95时经验似然（EL）和正态逼近（NA）的覆盖率（平均长度）

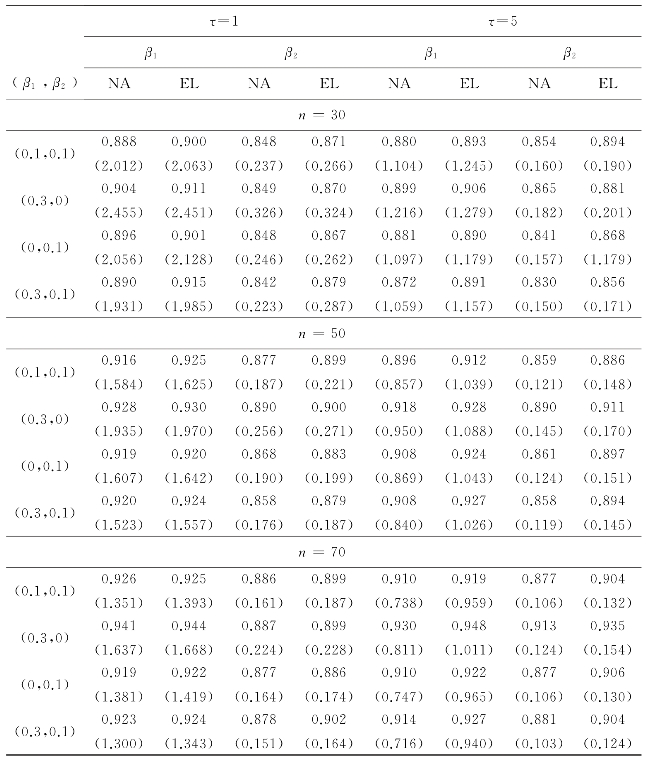
表6.2　在g（t）＝log（t），μ0（t）＝exp（t）下，置信水平为0.95时经验似然（EL）和正态逼近（NA）的覆盖率（平均长度）

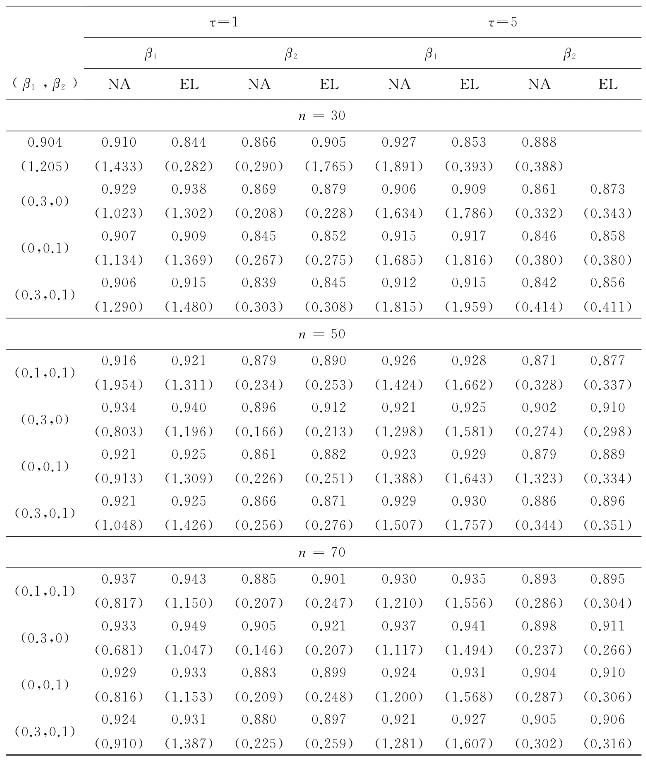
表6.3　在g（t）＝t2，μ0（t）＝exp（t）下，置信水平为0.95时经验似然（EL）和正态逼近（NA）的覆盖率（平均长度）