使用数值模拟验证有限样本条件下的β0和γ0估计方法

为了验证所提出的估计方法在有限样本容量下的表现，本节进行一些数值模拟.这里我们主要集中在β0和γ0的估计上.在下面的模拟中，受Li等（2010）的启发，我们也类似地考虑协变量Xi和Wi都为Bernoulli随机变量，其成功概率为0.5，并且最长的跟踪时间为τ，删失时间Ci由均匀分布（τ/2，τ）产生.设λ0（t）＝c/τ，c是一个常数，且Ni（t）是Poisson过程，其均值函数为：Λ（Ci|Zi）＝Λ0（Ci）（1＋exp{βWi}）-1exp{γXi}＝cCi（1＋exp{βWi}）-1exp{γXi}/τ并且观测时间是长度为ki的次序统计量，ki来自均匀分布U（0，Ci）.

表5.1给出了（β0，γ0）取不同的（0，0），（0.1，0），（0，0.1）和（0.1，0.1），τ为1或2时，样本量n在100和200之间变换，其中10%是治愈个体.利用重复迭代1000次得到模拟结果.表中包含有估计的BIAS，SSE，SEE和CP，其中BIAS为估计量的样本均值减去真实值，SSE为的样本标准差，SEE为的标准差估计的平均值，CP为θ0的95%经验覆盖率.从这些结果可以看出，BIAS接近于零，说明点估计是无偏的；SSE与SEE彼此接近，故我们的方差估计起到了很好的效果；CP这一经验覆盖率也十分接近我们提出95%的置信水平.综上，我们提出的估计是渐近无偏的，其方差估计和覆盖概率是合理的.

表5.1　含治愈个体复发事件模型的仿真结果

(www.xing528.com)

为了验证在有治愈个体存在的情况下，我们所提出的模型和估计方法与原来的有所不同，这里通过数值模拟来比较分析.把我们所提出的模型和估计方法与Lin等（2000）中的模型与方法都用到相同的复发事件数据中，计算出γ0的偏差，从而比较它们的优劣.表5.2中两个模型的参数设置除了我们模型对样本量n中有10%的治愈个体及多考虑协变量W（t）对复发率的影响，而原来模型则忽略这些，其他的二者均相同（都与表5.1的设置相同）.在表格中，BIAS和SSE分别表示所提出估计的偏差和估计的标准差，BIAS*和SSE*分别表示由Lin等（2000）中给出估计的偏差和估计的标准差.从数据对比的结果来看，在相同设定的情况下，BIAS与SSE分别比BIAS*与SSE*的绝对值更小，这说明在考虑协变量通过治愈率影响复发率时，我们对未知参数所提出的估计比Lin等（2000）方法更为合理.

表5.2　所提模型与忽略治愈个体模型中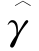的比较