由于治愈个体的生存时间肯定大于试验观测时间(也会被删失掉),所以怎样从复发事件的删失数据中识别出这些治愈个体就成了一个非常重要的任务.类似的问题在一般的生存数据中被提到,依据Maller等(1995,1996)的研究成果,当试验的观测时间(follow-up)足够长时,在实际应用中,通过Kaplan-Meier生存函数曲线去大体判断是否存在治愈个体就成为比较流行且有效的检验手段(Lai,2009).因此我们用累计发病次数曲线类似生存分析里的Kaplan-Meier函数曲线,在复发数据中对识别治愈者做如下标记,如图5.1所示,以横轴表示观察时间,纵轴表示个体i的累积发病次数,以累积发病次数趋于稳定来判定长期生存者的存在.
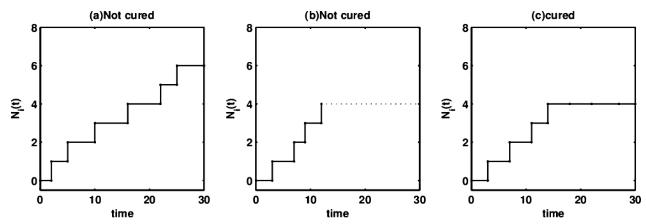
图5.1
图5.1(a)表明个体i为非治愈者.因为,曲线累计发病次数一直上升.(https://www.xing528.com)
图5.1(b)表明个体i为非治愈者.因为,数据中虽有一段趋于稳定的平台,但这是由于个体i随机删失后,此后数据收集不到,才使得累计发病次数不变.因此,不认为它是治愈者.
图5.1(c)表明个体i为治愈者.因为,在数据未随机删失的情况下累计发病次数有一段趋于稳定的平台.
本章结构如下:第5.2节第一部分,在原来半参数比例模型(5.1.1)回归事件的复发率基础上,我们利用Logistic模型回归治愈率部分,进而提出一类带有治愈率的半参数比率的新模型(5.2.1),来刻画协变量对事件复发率的影响.第5.2节第二部分,利用估计方程的思想,讨论我们模型中回归参数的估计.第5.3节研究这些估计的渐近性.第5.4节借助计算机Matlab软件,通过一些数值模拟来验证所提出的方法是有效的.第5.5节把所得的模型和方法应用到一组实际的纵向复发膀胱癌数据中.本文涉及的证明皆在第5.7节中给出.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




