在本节中,我们将使用与上面定义的相同的符号,并且所有极限均视为n→∞.假设g是次连续可微的函数.还假设Zi(t),H(.)和W(t)有界变化,并且W(t)几乎可以肯定地收敛于确定性函数w(t),t∈[0,τ].定义
令s0(t),s1(t),exk(t)和rk(t)分别表示S0(t;γ0),S1(t;γ0),![]() (t;θ0,γ0)和Rk(t;θ0,γ0).设
(t;θ0,γ0)和Rk(t;θ0,γ0).设![]() .首先,通过线性扩展g,我们有
.首先,通过线性扩展g,我们有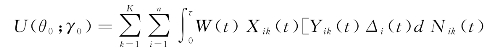
其中![]() 位于μ0k(t)和
位于μ0k(t)和![]() 之间.注意
之间.注意![]() 满足
满足
同样,θ=θ0和γ=γ0,(3.7.2)的线性展开会产生
其中![]() 位于μ0k(t)和
位于μ0k(t)和![]() 之间.通过使用函数中心极限定理(Pollard,1990,p53)和
之间.通过使用函数中心极限定理(Pollard,1990,p53)和![]() ,在t处可以得出
,在t处可以得出![]() .
.
因此,结合(3.1.1)和(3.7.3)和![]() 的一致收敛性,有
的一致收敛性,有
其中,
众所周知,
因此,
然后是
有
其中![]() .(3.7.2)关于γ的微分(https://www.xing528.com)
.(3.7.2)关于γ的微分(https://www.xing528.com)
其中,
令P*(θ,γ)=-n-1∂U(θ,γ)/∂γ′.因此,从(3.7.5)和(3.7.6)可以得出,在θ和γ处,P*(θ,γ)几乎处处地收敛于一个非随机函数P(θ0;γ0).用P表示P(θ0;γ0).然后
在(θ0,γ0)处,使用![]() 的泰勒展开,基于
的泰勒展开,基于![]() 的一致性和Lin等人(2000)的公式(3.7.5)有
的一致性和Lin等人(2000)的公式(3.7.5)有
其中
因此,由(3.7.4),(3.7.7)和多元中心极限定理有![]() 依分布收敛到正态随机向量,其均值为0,协方差矩阵为
依分布收敛到正态随机向量,其均值为0,协方差矩阵为
通过使用Lin等人(2000年)的公式中的方法.很容易看出Σ是由3.3节给定的![]() 一致地估计.
一致地估计.
(3.7.2)关于θ的微分有
其中
因此,由(3.7.8)和一些简单的代数得![]() 在θ处几乎处处收敛到非随机函数A(θ),其中
在θ处几乎处处收敛到非随机函数A(θ),其中
并且A(θ)由3.3节中给定的![]() 一致估计.在
一致估计.在![]() 处,
处,![]() 的泰勒展开为
的泰勒展开为
因此,从(3.7.7)和(3.7.9)可以得出,![]() 渐近地遵循均值零和协方差矩阵为A(θ0)-1ΣA(θ0)-1的正态分布,其中A(θ0)-1ΣA(θ0)-1由
渐近地遵循均值零和协方差矩阵为A(θ0)-1ΣA(θ0)-1的正态分布,其中A(θ0)-1ΣA(θ0)-1由![]() 一致估计.
一致估计.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




