我们进行了广泛的仿真研究,以评估所构建的推断过程的性能,重点是估计β和α.在研究中,我们假设Zi(t)是伯努利随机变量,成功概率为0.5,并且后续时间Ci是由均匀分布(τ/2,τ)生成的.为了生成观察过程,假定Ni1(t)和Ni2(t)是具有满足模型(3.2.1)的泊松过程.在这种情况下,给定Zi(t),观察次数![]() 遵循泊松分布,均值为
遵循泊松分布,均值为![]() .观察时间(tik,1,...,
.观察时间(tik,1,...,![]() 是来自(0,Ci)上的均匀分布的大小为
是来自(0,Ci)上的均匀分布的大小为![]() 的随机样本的有序统计量.
的随机样本的有序统计量.
为了生成面板计数Yik(tik,l),我们假设
![]()
并给出![]() 和
和![]() 遵循泊松分布,均值函数分别为
遵循泊松分布,均值函数分别为
![]()
和
![]() (https://www.xing528.com)
(https://www.xing528.com)
j=1,...![]() ,k=1,2,i=1,...,n..这里tik,0=0和Qi是来自伽玛分布的随机样本,均值1,方差0.1.关于函数g和μ0k,我们考虑了许多选择,包括对于g有,g(t)=t,g(t)=t2和g(t)=log(t),对于μ0k有μ0k(t)=t,μ0k(t)=t1/2和μ0k(t)=exp(t).对于所有情况,我们取H(Fikt)=Nik(t-),W(t)=1,n=100或300.下面报告的结果基于500次重复.
,k=1,2,i=1,...,n..这里tik,0=0和Qi是来自伽玛分布的随机样本,均值1,方差0.1.关于函数g和μ0k,我们考虑了许多选择,包括对于g有,g(t)=t,g(t)=t2和g(t)=log(t),对于μ0k有μ0k(t)=t,μ0k(t)=t1/2和μ0k(t)=exp(t).对于所有情况,我们取H(Fikt)=Nik(t-),W(t)=1,n=100或300.下面报告的结果基于500次重复.
表3.1给出了基于模拟数据的β和α估算结果,其中模拟数据为g(t)=t,μ01(t)=t,μ02(t)=t1/2,λ01(t)=20/τ,和λ02(t)=15/τ.结果包括点估计的样本均值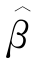 和
和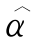 减去其真实值所得出的估计偏差(Bias),以及估计标准误差的样本均值
减去其真实值所得出的估计偏差(Bias),以及估计标准误差的样本均值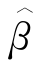 和
和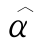 (SEE),
(SEE),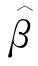 和
和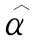 (SSE)的抽样标准差以及95%的经验值
(SSE)的抽样标准差以及95%的经验值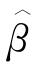 和
和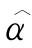 的覆盖概率(CP).从表中可以看出,点估计似乎是无偏的,并且SEE和SSE彼此非常接近,这表明建议的方差估计似乎工作良好.同样,覆盖率概率是合理的并且与名义水平一致,并且正如预期的那样,随着样本量的增加,方差的估计值变得更小.
的覆盖概率(CP).从表中可以看出,点估计似乎是无偏的,并且SEE和SSE彼此非常接近,这表明建议的方差估计似乎工作良好.同样,覆盖率概率是合理的并且与名义水平一致,并且正如预期的那样,随着样本量的增加,方差的估计值变得更小.
表3.1 在g(t)=t,μ01(t)=t,μ02(t)=t1/2,λ01(t)=20/τ,和λ02(t)=15/τ的情形下,β和α的估计结果
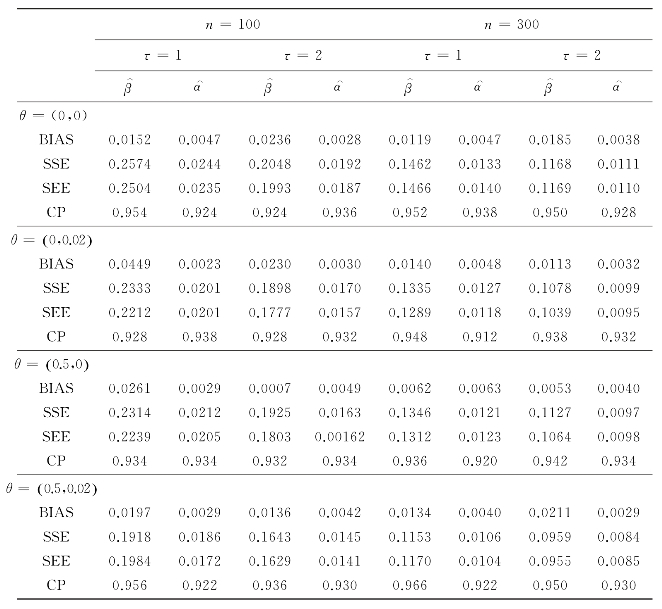
表3.2和表3.3给出的结果也与根据表3.1使用的设置下获得的β和α的估计有关,除了一些基本功能.具体来说,在表3.2中,我们使用g(t)=log(t),μ01(t)=μ02(t)=exp(t),λ01(t)=λ02(t)=10/τ,而对于表3.3,我们使用g(t)=log(t),μ01(t)=exp(t),μ02(t)=exp(t1/2),λ01(t)=10/τ和λ02(t)=6/τ.可以很容易地看出,表3.2和表3.3得出的结论与表3.1中给出的结论相似,并且再次表明,所提出的推理程序在实际情况下似乎表现良好.除了此处介绍的结果外,我们还考虑了其他设置,使得Zi遵循正态分布,并且观察过程是由非均匀泊松过程生成的.获得的结果与上述相似.
表3.2 在g(t)=log(t),μ01(t)=μ02(t)=exp(t),λ01(t)=λ02(t)=10/τ的情形下,β和α的估计结果
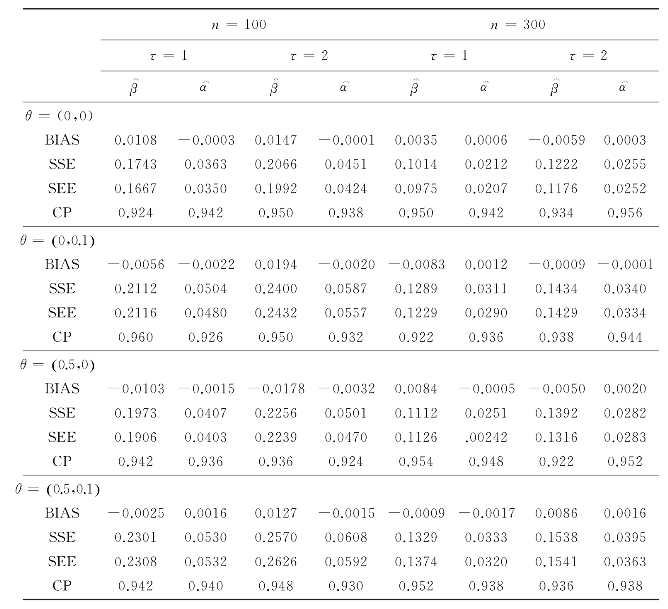
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




