方式进行推断如何推断回归参数和其他参数？

在本节中，我们将介绍回归参数β和α以及其他参数的估计过程.为此，设β0，α0和γ0表示β，α和γ的真实值.设Xik（t）＝（Zi（t）′，H（Fikt）′）′，θ＝（β′，α′）′，θ0＝（β′0，α′0）′.定义

i＝1，...，n.然后在模型（3.2.1）和（3.2.2）下，Mikt（；β0，α0，γ0）是零均值随机过程.这表明，如果已知β，α，γ和Λ0k，则可以通过解来估计μ0k（t）

通过以下估计方程估计θ

其中W（t）是可能与数据相关的权重函数.

通常来说，γ和Λ0k（t）是未知的.幸运的是，我们在Nik（t）上有重复事件数据，在这种情况下，解决方案给出了γ的一致估计量，例如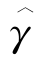，估计方程

（Andersen等，1993；Cook and Lawless，2007）.在上述，γ）/S0（t；γ）

j＝0，1...此外，Λ0k（t）可以估算为

将γ替换为.

设和表示由估计方程（3.3.1）和（3.3.2）给出的θ和μ0k（t）的估计，其中将γ和Λ0k（t）分别替换为和.然后按照Lin等（2001）和Sun等（2005）的讨论.可以证明，对于大的n，和始终存在，并且是唯一且一致的.为了建立的渐近正态性，定义

上述中，为向量υ.然后可以证明，当n→∞时，-θ0）的渐近正态分布的均值为零，协方差矩阵可以由一致估计，其中

该证明在附录3.7中进行了概述.

为了确定和，设s1＜s2＜...＜sJ表示{tik，l，l＝1，...，mik；i＝1，...，n；k＝1，...，K}的有序观测时间.然后可以首先在等式（3.3.1）中推导处，可以将其重写为

j＝1，...，J.将μ0k（t）替换为，等式（3.3.2）的形式为

可以很容易地看出，和没有封闭形式，并且一些迭代算法具有用于求解上述方程式.但是，对于某些特殊函数g，这些估计量的确定非常简单.例如，假定g（t）＝tη，其中η是一个正常数.在这种情况下，给定明确表达式

变为(www.xing528.com)

其中

如果我们取g（t）＝log（t），则估计量可以得到一个封闭形式

在这种情况下，我们有

其中

产生

也就是说，具有封闭形式.

实际上，对于给定的数据集，需要在模型（3.2.2）中选择函数g.与纵向数据分析（Lin等，2001）和故障时间数据分析（Zhang等，2005）一样，这通常是一个非常困难的问题.常见的策略是尝试几种选择并比较获得的结果.下面对此进行了更多评论和讨论.我们还指出，尽管模型（3.2.2）包括Sun等人（2005年）提出的模型作为一个特例，回归参数的估计并没有减少到Sun等人（2005）给出的估计.

与函数g的选择有关的一个问题是用给定的g评估模型（3.2.2）的适当性，或进行拟合优度检验.注意，人们可能也想评估模型（3.2.1），为此，Lin等人（2000）给出了这种方法.可以应用.为了评估模型（3.2.2）的适当性，请遵循Sun等（2007a），可以考虑以下残差的累积总和

其中I{Xik（u）≤x}表示Xik的每个分量都不大于x的相应分量.注意，在模型（3.2.2）下，F（t，x）预计将在0附近随机波动.然后，可以基于最高统计量supt，x|F（t，x）|构造拟合优度检验.

要确定上述拟合优度检验的p值，定义

其中

通过遵循类似于Lin等（2000年）的论点.可以证F（t，x）的零分布可以通过零均值高斯过程来近似

此外，可以通过零均值高斯过程分布Gi来近似估计F（t，x），其中（G1，...，Gn）是独立于观察数据的独立标准正态变量.因此，通过反复生成标准正态随机样本（G1，...，Gn）固定观测数据，将sup0≤t≤τ，x|F（t，x）|的观测值与的大量实现比较，可以得到p值.