我们进行了广泛的仿真研究,以评价所构建的推断过程的性能,重点是估计β和α.在研究中,我们假设Zi是伯努利随机变量,成功概率为0.5,并且跟踪时间Ci是根据(τ/2,τ)上的均匀分布生成,其中τ=1或2或3或4.
对于生成观察过程,假定Ni(t)是泊松过程,其中λ0(t)=c/τ,其中c是常数.在这种情况下,给定Zi,观测值![]() 遵循泊松分布,均值为
遵循泊松分布,均值为

以及观察时间![]() 是来自样本的大小为
是来自样本的大小为![]() 的随机样本的阶次统计量(0,Ci)上的均匀分布.为了生成面板计数Yi(ti,j),我们考虑了两种情况,对于这两种情况,我们假设:
的随机样本的阶次统计量(0,Ci)上的均匀分布.为了生成面板计数Yi(ti,j),我们考虑了两种情况,对于这两种情况,我们假设:
![]()
其中ti,0=0.对于第一种情况,假设![]() 和
和![]() 遵循泊松分布,其分别均值
遵循泊松分布,其分别均值
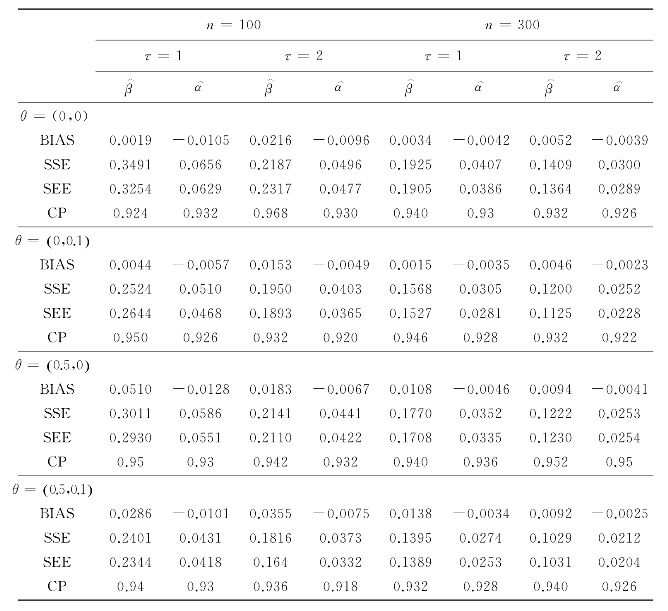
表2.1 来自泊松过程的模拟数据,转换函数g(t)=t下,β和α的估计结果
函数为![]() 和
和![]()
![]() .
.
在第二种情况下,假定![]() 和
和![]() 遵循带有条件均值函数的混合泊松分布,给定ei分别有(https://www.xing528.com)
遵循带有条件均值函数的混合泊松分布,给定ei分别有(https://www.xing528.com)

j=1,...![]() .这里的ei是来自伽马分布的随机样本,平均值为1,方差为0.02.关于函数g和μ0,我们考虑了许多选择,对于g有g(t)=t,g(t)=t2和g(t)=log(t).对于μ0有μ0(t)=t,μ0(t)=t1/2和μ0(t)=exp(t).对于所有情况,我们取H(Fit)=Ni(t-),W(t)=1和n=100或300.由于问题的复杂性因此算法的速度一般500次重复运行,结果显示在下面表2.1和表2.2中的.但是我们在表2.3中用的1000次重复运行因为估计值具有封闭形式.
.这里的ei是来自伽马分布的随机样本,平均值为1,方差为0.02.关于函数g和μ0,我们考虑了许多选择,对于g有g(t)=t,g(t)=t2和g(t)=log(t).对于μ0有μ0(t)=t,μ0(t)=t1/2和μ0(t)=exp(t).对于所有情况,我们取H(Fit)=Ni(t-),W(t)=1和n=100或300.由于问题的复杂性因此算法的速度一般500次重复运行,结果显示在下面表2.1和表2.2中的.但是我们在表2.3中用的1000次重复运行因为估计值具有封闭形式.
表2.1给出了基于模拟数据的β和α的估算结果,其中模拟数据和g(t)=t,μ0(t)=t,并且θ=(β,α)的真实值分别为(0,0),(0,0.1),(0.5,0)或(0.5,0.1).结果包括点估计的样本均值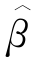 和
和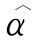 减去其真实值所得出的估计偏差(Bias),以及估计标准误差
减去其真实值所得出的估计偏差(Bias),以及估计标准误差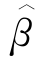 和
和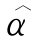 (SEE),
(SEE),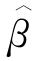 和
和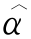 (SSE)以及95%
(SSE)以及95% 和
和 的经验覆盖率百分比(CP).从表中可以看出,点估计似乎是无偏的,并且SEE和SSE彼此非常接近,这表明建议的方差估计似乎工作良好.此外,覆盖率概率是合理的并且与名义水平一致,并且正如预期的那样,随着样本量的增加,方差的估计值变得更小.
的经验覆盖率百分比(CP).从表中可以看出,点估计似乎是无偏的,并且SEE和SSE彼此非常接近,这表明建议的方差估计似乎工作良好.此外,覆盖率概率是合理的并且与名义水平一致,并且正如预期的那样,随着样本量的增加,方差的估计值变得更小.
表2.2 来自混合泊松过程的模拟数据,转换函数g(t)=t下,β和α的估计结果
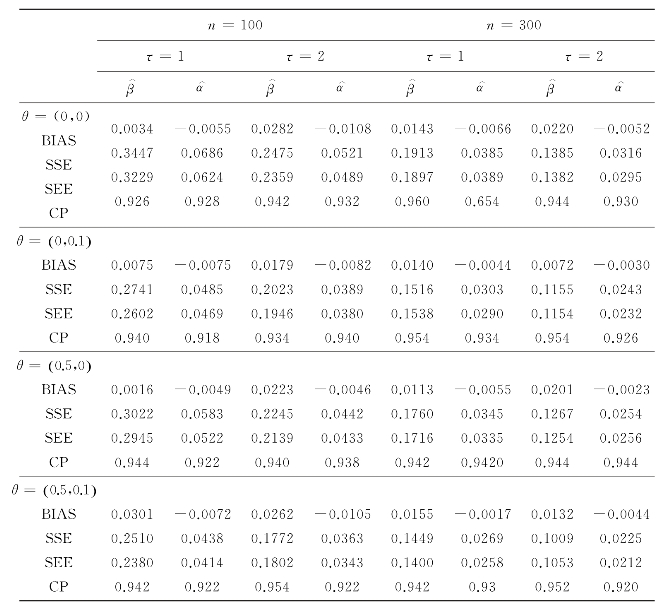
表2.3 来自泊松过程的模拟数据,转换函数g(t)=logt下,β和α的估计结果

表2.2和2.3中给出的结果也与在不同设置下获得的β和α的估计有关.具体而言,表2.2考虑了从混合泊松分布生成面板计数数据且其他设置与表2.1相同的情况.在表2.3中,我们假定g(t)=log(t)和μ0(t)=exp(t),其他设置与表2.1类似.
可以看出,表2.2和表2.3中的结果与表2.1中的结果相似,并且再次表明,所提出的推理过程对于实际情况似乎表现良好.如上所述,已经研究了许多其他设置.例如,我们还研究了Zi服从正态分布,或者观察过程是由非均匀泊松过程生成的情况.全部结果得到的结论相似.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




