水弹性模型要求原型与模型应同时满足几何相似、水力学条件相似及结构动力学条件相似。根据水力学条件相似准则,应按重力相似律来设计模型。根据结构动力学条件相似准则,还应要求结构模型材料满足密度比尺(结构物容重比尺为1)、弹性模量比尺(弹性模量比尺等于几何比尺),以及满足等阻尼比、等泊松比条件,并合理地选取水域和地基模拟范围以保证结构动力响应系统的相似。
关于地基模拟范围的分析(本项研究仅讨论地基深度及宽度的模拟范围对自振频率的影响)是结合三峡左导墙,共建立了6个三维有限元模型,通过模拟计算进行的。
计算结果表明:自振频率随地基模拟深度的增大而减小,当地基模拟深度从80m变化到0时,低阶振型频率变化很小,在3%以内;高阶振型频率变化也可控制在5%以内。当地基模拟宽度从60m变化到0时,低阶振型频率变化也很小,只在3%以内;其高阶振型频率变化可控制在5%以内。
水弹性模型在制作过程中,主要是以容重和弹模作为控制指标,通过计算对这两个因素的影响进行了研究;而对阻尼比和泊松比这两个因素的影响则考虑用数模结果修正。
通过计算表明,地基材料容重的小范围变化,对导墙自振频率基本没有影响,但导墙材料容重对其自振频率的影响较大,在设计模型时应予以充分重视。
计算还表明,地基材料及导墙材料的弹模变化对其自振频率的影响均较为明显,故在设计模型时也应予以重视。
除探讨了模型范围及材料对自振频率的影响外,他们还对这两个因素对导墙的动力响应(导墙顶部的动位移)影响进行了计算比较。结果表明:模型的模拟范围对导墙的动位移影响较小;导墙动位移响应随地基材料容重变化较小,但随导墙自身材料容重的变化较大。地基和导墙的弹模对导墙的动力响应是明显的。由以上分析可知在模型制作中应严格控制导墙材料的容重和地基及导墙材料的弹模。
本试验设计的模型几何比尺为1∶100,模拟长度为262.75m,第1~12段各长20m,第13段长22.75m,其中9段、5段采用加重橡胶来模拟原型材料,制成的模型材料的平均弹模为318MPa(按弹模比尺要求应为340MPa),离差σ=20MPa;平均容重为2.30万N/m3(按容重比尺要求应为2.40万N/m3),离差σ=430N/m3;由于模型材料特性未能满足相似律要求引起的各种误差将通过反馈分析进行修正。(https://www.xing528.com)
三峡水利枢纽的左、右厂坝导墙在顺水流方向上均设有伸缩缝,将导墙分成独立工作的单个墙块,左导墙除最后一段长为22.75m外,其余均为20m一段(见图7.1);右导墙模拟区间则分别为15m或20m一段(见图7.2)。模型的地基模拟深度和向两岸延展宽度均控制在10m左右。

图7.1 厂坝左导墙布置(单位:m)
(a)左导墙纵剖面图;(b)左导墙横剖面图
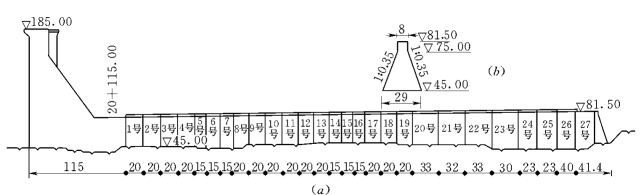
图7.2 厂坝右导墙布置(单位:m)
(a)右导墙纵剖面图;(b)右导墙横剖面图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




