A3C版DDPG的伪代码如下。
首先，设置一个全局共享的目标网络，Actor的参数为θ，Critic的参数为θv，下标v的意思是“Value”（表示用它来做估值）。每个Agent的Actor参数为θ′，对应的Agent的Critic网络的参数是θ′v。这个结构是对称的，很容易记忆。然后，仍旧是全局计步器和本地线程计步器（分别初始化为T＝0和t＝1）。开启一个循环，直到T＞Tmax。
循环内部的工作流程也比较简单。
首先，把全局目标网络中Actor的参数的θ更新量dθ设置为0，把Critic的参数θv的更新量dθv设置为0。同时，把线程本地的Actor的参数θ′赋值为目标网络的Actor的参数θ的值，把线程本地的Critic的参数θ′v赋值为目标网络的Critic的参数θv的值。
这里有一个循环，就是在当前线程中让机器人不停地玩游戏，直到通关、游戏结束或者达到试探步数的上限（t－tstart＝tmax）为止。在它“生存”的过程中，使用策略π（at｜st；θ′）输出动作，也就是用本地的Actor网络来输出动作。同时，要记录相关的s→a→r→s′。
以第二个循环结束时遇到的状态st为研究对象，先计算估值。使用表达式
0表示st为终止状态Terminal，V（st，θ′v）表示其他状态。这一点，不仅和DQN不一样，也和DDPG不一样。DQN在很大程度上还要指望在处于Terminal状态时所赋予的一个很大或者很小的奖励值，以训练机器人找到方向，但是在这里，只要游戏结束，得分都是0。
在这里，学习与更新也构成了一个循环，循环范围是t－1到tstart。可以看出：t这个计步器的值是在当前线程中不断增加的，而且从不清零；tstart是在机器人玩游戏之前记录的步数，所以当机器人开始玩游戏之后，t－1的值肯定要比tstart的值大一些。这个循环可以认为是一个从大到小的倒序循环，即先处理距现在最近的那个时间片。这样处理的目的，主要是计算更为方便，因为根据蒙特卡罗法，某个时间片t的状态估值是逐层“打折扣”的：
如果从后面开始算，就可以不使用递归的方式来表示，而直接使用(www.xing528.com)
来表示。经过t－1到tstart的循环过程，自然就能得到上面那个Gt的表达式。
接着是梯度更新：
这两个公式表示对目标网络中的Actor的参数θ的更新大小，是一个累积的量，从t－1到tstart的每个时间片都要经过这样的累积。每次累积的量是本地线程使用的Actor的θ′梯度，这个梯度的大小是
然后，在外面取对数。π（ai｜si；θ′）是一个概率值，（R－V（si；θ′v））是估值的误差。
再看一下Critic网络的更新，只是一个大小为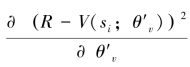
的梯度。也就是说，θ的更新量dθ是沿着策略π（ai｜si；θ′）的参数θ′的变化方向变化的，θv的更新量dθv是沿着减小估值误差的θ′v的变化方向变化的。因为π（ai｜si；θ′）的取值范围仅为0到1，直接求梯度会使其消失，所以在这里也算使用了一个Trick，即在求对数之后，原来在0到1之间的分布直接变成了在正无穷到0之间的分布，梯度（偏导i数）一下子变大了。由于有梯度就会有更新，网络学东西的速度也会快一些。
在循环的最后，会进行一次更新。全局性的Actor网络和Critic网络的更新，相当于只要机器人“玩”过一个Episode，就让全局网络对它所学到的东西进行一次学习，且更新是以Episode为单位进行的。
【注释】
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
