人工智能原理：K-均值聚类

K－均值算法的最早想法由Hugo Stein haus于1957年提出^[2]，而“KMeans”名称的出现则是在1967年，Stuart Lloyd于1957年在Bell实验室给出了标准K－均值聚类算法，并于1982年正式发表于IEEE Transactions on Information Theory。

由于算法实现简单，计算复杂度和存储复杂度低，对很多简单的聚类问题可以得到令人满意的结果，K－均值算法已经成为最著名和最常用的样本聚类算法之一。

（一）K－均值算法

K－均值算法的目标是将n个样本依据最小化类内距离的准则分到K个聚类中

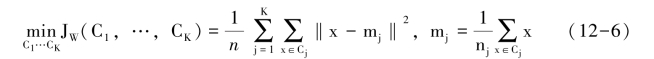
直接对上述类内距离准则优化存在一定的困难。现在换一个思路来讨论这个优化问题，首先假设每个聚类的均值m1，…，mK是固定已知的，那么这个优化问题就很容易求解了，因为现在问题变为每一个样本x选择加入一个聚类Cj，使得类内距离准则最小，很显然如果，应该将x放入聚类Ci，这样可以使得JW最小；然而已知每个聚类的均值m1，…，mK的假设是不成立的，因为在知道每个聚类包含哪些样本之前是无法求得样本均值的，聚类的均值只能根据这个聚类中所有的样本求得。

由上面的讨论看到优化类内距离准则的困难在于聚类的均值m1，…，mK和每个聚类包含的样本之间，如果知道其中的一个，就可以很容易地计算另外一个，然而实际情况是两者都不知道。K－均值算法的思想是首先对其中之一做出假设，例如给出每类均值的一个猜想值m≫1，…，m≫K，然后根据均值的猜想值确定每个样本的类别属性，得到对聚类结果的猜想C≫1，…，C≫K；由于样本的分类结果依据的是猜想的均值，因此并不是一个准确的结果，但可以作为猜想值用于更新对均值的猜想。这样就得到了一个交替的迭代过程：

迭代过程可以一直持续下去，直到均值或样本的分类结果不再变化为止，此时可以认为算法收敛到了一个对JW的优化聚类结果。

（二）算法的改进

K均值是一种简单实用的聚类分析算法，针对基本算法存在的问题，可以从如下几个方面进行改进。

1.初始值的选择

算法能否收敛于最优解取决于初始值的设置，随机选择K个训练样本作为初始均值并不能保证算法的收敛性能。

（1）如果对聚类样本的结构有一定的先验知识，知道各个聚类所处的大致位置，那么可以利用先验知识设定初始的聚类均值。

（2）K－均值算法中样本的分类和均值的估计这两个过程是迭代完成的，因此初始的时候既可以随机设定聚类的均值，也可以随机地将样本集划分为K个聚类。

（3）在样本集中选择相互之间距离最远的K个样本，这些样本处于不同聚类的可能性很大，如果以这K个样本作为初始的聚类均值，有助于算法收敛到一个较好的聚类结果。样本集中相距最远的K个样本可以采用类似最大最小距离算法的方式得到。

2.聚类数的选择

聚类数的选择同样是一个影响聚类结果的重要因素，只有设定了正确的聚类数才有可能得到好的聚类结果，然而遗憾的是到目前为止还没有一个简单的方法能够确定出训练样本集合中包含的聚类数量。一种可行的方法是采用试探的方式确定聚类数，从少到多设定不同的聚类数，由K－均值算法得到相应的聚类结果，然后进行聚类有效性的检验，从中选择出适合的聚类数和聚类结果。

3.距离函数的选择(www.xing528.com)

K－均值算法优化的类内距离准则是以欧氏距离度量样本之间的相似程度，这就要求每个聚类的样本大致成团型分布。如果每个聚类的样本分布不满足此要求时，需要考虑采用其他的距离度量方式，如图12－2中的样本呈现椭球形分布，适合采用马氏距离作为样本与聚类之间相似性的度量：

使用不同距离度量时需要注意的是描述每个聚类的参数是有差异的。欧氏距离度量，可以用每个聚类的均值m，作为参数描述；而马氏距离则需要每个聚类的均值m，和协方差矩阵∑1。算法可以初始于样本的随机聚类划分，然后计算每个聚类的均值和协方差矩阵，每轮迭代时根据样本的重新划分结果更新均值和协方差矩阵。如果采用的是街市距离，描述聚类的参数是中值矢量，每一轮迭代更新时需要分别计算每一维特征的中值，然后将所有中值组合成中值矢量，此算法也被称为K－Median算法。

图12-2　适合采用马氏距离度量的聚类

4.K－Medoids算法

在一些应用中，需要聚类的对象不是以特征矢量方式描述的，而是采用序列、图等其他方式描述的。如果能够计算出两个模式之间的相似程度，也可以使用K均值算法实现聚类。初始时随机选择K个模式代表每个聚类，计算样本与K个代表模式的相似度，完成对样本的分类，然后在每个聚类的样本中寻找一个与其他样本相似度之和最大的样本更新代表模式。此算法一般被称为K－Medoids算法。

5.模糊K－均值

需要聚类的样本集在各个聚类之间并不一定是能够严格分开的，很多情况下聚类之间是存在交叠的。K－均值算法的每一轮迭代中严格地将每个样本分类为某个聚类，这种方法一般称为是“硬分类”。然而处于交叠区域的样本实际上很难判断它属于哪个聚类，一个合理的想法是在迭代过程中采用“软分类”或“模糊分类”来代替“硬分类”，这就发展出了模糊K－均值算法。

在“硬分类”中，样本xi与聚类Cj之间的关系可以用集合的示性函数来描述：

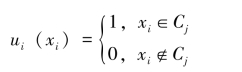
而在“模糊分类”中，认为xi属于C1，…，CK中的任何一个聚类，只不过属于的程度不同，一般可以用隶属度uij表示xi属于聚类Cj的程度。模糊K－均值算法优化的聚类准则函数是

同时约束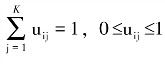：，其中b＞1为控制不同聚类混合程度的可调参数。

使用最优化方法可以推导出如下结论，当聚类的均值＋m1，…，mk固定时，隶属度的最优解为

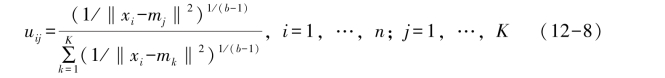
当隶属度u11，…，uRK固定时，均值的最优解为

在算法实现中，可以设定一个容忍误差阈值ε，当时，认为第t轮迭代的隶属度uij（t）相对于t－1轮选代的隶属度uij（t－1）变化已经很小终止迭代；如果希望算法输出如同K－均值算法一样的“硬聚类”结果，可以将每个样本划分到其隶属度最大的聚类。