（一）C－GRU模型预测准确性的评估
采用标准化的平均绝对误差NMAE（Normalized Mean Absolute Error）与标准化的均方根误差NRMSE（Normalized Root Mean Square Error）作为模型准确性的评估标准。NMAE与NRMSE的公式表达如下：
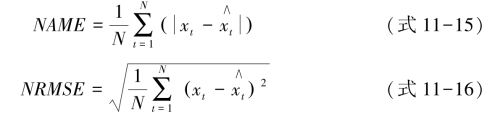
其中，xt为t时刻标准化之后的风功率真实值；
为t时刻经过C－GRU模型得出的标准化的风功率预测值；N为测试集中的数据点数。
（二）C－GRU模型的实验分析
通过实验发现，当模型风功率输入时间序列维度为16时预测结果最好，预测期间设定为4 h，即对于某一特定时刻t，采用其前4～19 h的真实风功率数据以及t时刻风速、风向和风的经纬分量的数值天气预报预测值作为输入数据预测其4 h后时刻的风功率。经过对不同的模型结构及参数进行调参试验，最终模型参数如下：
（1）卷积神经网络：卷积神经网络中包含2层卷积层，第一层中有64个特征探测器（1×4维向量），第二层中有32个特征探测器（1×3维向量），它们的激活函数都为ReLu。
（2）GRU神经网络：本书中模型包含5层GRU单元，经过试验测试调参，最终设定每一层中的隐含神经元数分别为64、128、64、32和16。
（3）全连接层：一个单一神经元的全连接层作为C－GRU风功率预测模型的输出层，它输出的结果即为t时刻风功率的预测值。
C－GRU模型拥有最小的NMAE值与NRMSE值，即C－GRU模型有最高的预测准确度。在与GRU神经网络的比较中发现，C－GRU模型的准确度有明显提升，这说明卷积神经网络具有很好的数据特征捕捉和数据降维的功能。从不同风速情况下的误差对比中发现，当风速波动较大时，模型的预测误差均会明显增加，但C－GRU模型的误差波动是最小的，在一定程度上证明了C－GRU模型的鲁棒性和适应性。
为了探究C－GRU风功率预测模型的预测结果与模型网络深度的关系，可以进行预测误差与网络层数的敏感度分析。
(www.xing528.com)
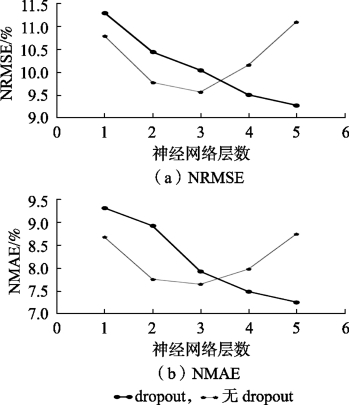
图11-13 预测误差随网络层次的变化
如图11－13所示，在没有施加dropout的情况下，模型在层数为3时达到最好的预测结果（NRMSE为9.64%，NMAE为7.75%）。但随着网络层数的继续增加，模型出现了严重的过拟合现象，当网络层数增加到5时，模型的预测结果比单层网络还要差，这是由于随着网络结构的深化，模型参数变得冗余而复杂，但短期风功率预测的输入数据形式单一且缺乏变化，从而造成的过拟合现象。但当增加dropout后，模型的预测效果随着网络层数的增加并没有衰减，故而在一定程度上减轻了模型的过拟合现象。
为了进一步比较C－GRU模型、LSTM神经网络模型与GRU神经网络模型在短期风功率预测中的效率和性能，可以针对不同的输入时间序列的长度，对三者的预测准确度和训练时间进行了实验比较。为了确保实验的准确性与合理性，三者均采用相同神经元数和隐含层数，并且使用相同的学习率和迭代次数。
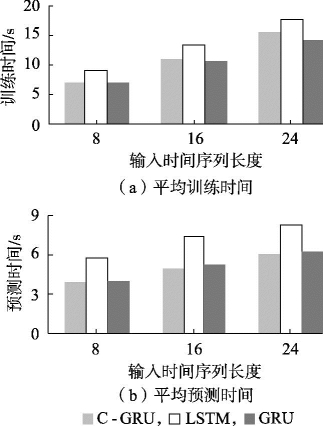
图11-14 不同输入时间序列长度下单位时期平均训练时间和平均预测时间
图11－14为不同输入时间序列长度下单位时期的平均训练时间和平均预测时间，从中可以看出，在输入时间序列长度分别为8、16和24的情况下，C－GRU模型和GRU模型的训练时间与预测时间均小于LSTM模型。
具体而言，LSTM模型的平均训练时间约为C－GRU模型的1.27倍，而在测试集上的平均预测时间约为C－GRU模型的1.36倍，这说明在短期风功率预测问题上，C－GRU神经网络比LSTM神经网络有更高的效率和更好的性能，这也与GRU网络舍弃LSTM模型中输入门、输出门、遗忘门的复杂结构，而以重置门、更新门代替的简化结构相呼应。
对比图11－14（a）、（b）可以发现，C－GRU模型的训练时间比GRU模型长，但预测速度比GRU模型快，这说明卷积神经网络在处理原始数据的训练过程中，卷积计算会占用较长的时间，而在预测过程中，GRU神经网络使用经过卷积神经网络降维后的数据，预测时间会降低，并且这种现象会随着输入向量维度的增加而愈发明显。
【注释】
[1]辛阳，刘治，朱洪亮，孔令爽.大数据技术原理与实践[M].北京：北京邮电大学出版社，2018：139.
[2]谢平，邹传伟.FINTECH解码金融与科技的融合[M].北京：中国金融出版社，2017：145.
[3]牛哲文，余泽远，李波，唐文虎.基于深度门控循环单元神经网络的短期风功率预测模型[J].电力自动化设备，2018，38（5）.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
