自21世纪,卷积神经网络开始被成功地大量用于检测、分割、物体识别以及图像的各个领域,这些应用都是使用了大量的有标签数据,比如交通信号识别、生物信息分割、面部探测、文本和行人以及自然图形中的人的身体部分的探测。近年来,卷积神经网络的一个重大成功应用是人脸识别,已经被用于几乎全部的识别和探测任务中。
燕乐存在贝尔实验室设计了一种基于卷积神经网络的手写数字识别系统LeNet-5。该算法具有很高的准确性,美国大多数银行当年用它识别支票上面的手写数字,达到了商用地步。
LeNet-5共有7层,有两个卷积层和两个全连接层。每个卷积层包括卷积、非线性激活函数映射和下采样三个步骤。除了输入层,每层都包含可训练参数(连接权重),如图9-4所示。LeNet-5在两个卷积层上使用了不同数量的卷积核,第一层是6个,第二层是16个。
输入图像为32×32。这样能够使一些重要特征如笔画、断点或角点能够出现在最高层特征监测子感受域的中心。
C1层是一个卷积层,由6个特征图构成。这之间有个单通道滤波器5×5×1→6,stride=5。滤波器大小为5×5×1=25,有一个可加偏置,6种滤波器得到C1的6个特征图。通过卷积运算,可以使原信号特征增强并且降低噪音。特征图中每个神经元与输入中5×5的邻域相连。特征图的大小为28×28,这样能防止输入的连接掉到边界之外。C1有(5×5×1+l)×6=156个可训练参数,156×(28×28)=122304个连接。
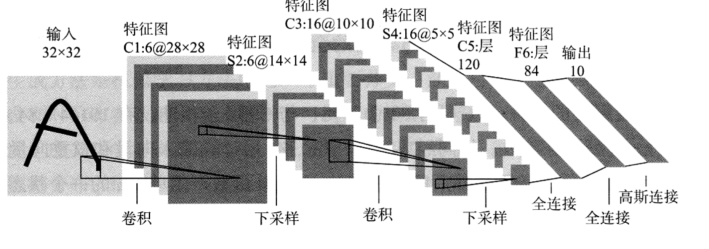
图9-4 卷积神经网络
S2层是一个下采样层,有6个14×14的特征图。特征图中的每个单元与C1中相对应特征图的2×2邻域相连接。C1层每个单元的4个输入相加,乘以一个可训练参数,再加上一个可训练偏置可得到S2层。每个单元的2×2感受野并不重叠,因此S2中每个特征图的大小是C1中特征图大小的1/4(行和列各1/2)。S2层有6×(1+1)=12个可训练参数和14×14×6×(2×2+1)=5880个连接。(https://www.xing528.com)
C3层也是一个卷积层,同样通过5×5的卷积核去卷积层S2,然后得到特征图map有10×10个神经元,但是它有16种不同的卷积核,所以就存在16个特征映射。
这里需要注意的是,C3中的每个特征映射并不都连接到S2中的所有特征映射,将连接的数量保持在合理范围内而且使不同的特征图有不同的输入,迫使它们抽取不同的特征。这里用组合模拟人的视觉系统,底层的结构构成上层更抽象的结构,如边缘构成形状或者目标的部分。
例如,C3的前6个特征图以S2中3个相邻的特征图子集为输入,接下来6个特征图以S2中4个相邻特征图子集为输入。后续3个特征图以不相邻的4个特征图子图为输入,最后1个特征图以S2中所有特征图为输入。这样C3层有1516个可训练参数和151600个连接。
S4层是一个下采样层,由16个5×5大小的特征图构成。特征图中的每个单元与C3中相应特征图的2×2邻域相连接,同C1和S2之间的连接一样。S4层有16×(1+1)=32个可训练参数(每个特征图9-10个因子和一个偏置)和2000个连接。
C5层是一个卷积层,有120个特征图。每个单元与S4层的全部16个单元的5×5邻域相连。由于S4层特征图的大小为5×5,同滤波器一样,故C5特征图的大小为l×l:这构成了S4和C5之间的全连接。C5层有120×(16×5×5+1)=48 120个可训练连接。
根据输出层的设计,F6层有84个单元,与C5层全相连,有10164(84×121(120+1))个可训练参数。如同经典神经网络,F6层计算输入向量和权重向量之间的点积,再加上一个偏置,然后将其传递给sigmoid函数产生单元i的一个状态。
输出层由欧氏径向基函数(euclidean radial basis function)单元组成,每类一个单元,每个有84个输入。径向基函数是一个取值仅仅依赖于离原点距离的实值函数,欧氏距离是其中一个实例,即每个输出RBF单元计算输入向量和参数向量之间的欧式距离。输入离参数向量越远,RBF输出的越大。假设x,x0∈RN,以x0为中心,x到x0的径向距离为半径所形成的‖x-x0‖构成的函数系满足K(x)=0,Il x-‖x-x0‖称为径向基函数。常用的径向基函数有高斯分布函数等。[1]
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




