感知器模型及其分类功能

感知器即单层神经网络，或者叫作神经元，是组成神经网络的最小单元。^[1]它是美国学者罗森布拉特（Rosenblat）在研究大脑的存储、学习和认知过程中于1957年提出的一类具有自学习能力的神经网络模型。根据网络中拥有的计算节点的层数，感知器可以分为单层感知器和多层感知器。

（一）单层感知器

单层感知器是一种只具有单层可计算节点的前馈网络，其网络拓扑结构是单层前馈网络（见图8－1）。在单层感知器中，每个可计算节点都是一个线性阈值神经元。当输入信息的加权和大于或等于阈值时，其输出为1，否则输出为0或－1。

图8-1　单层前馈网络结构

由于单层感知器的输出层的每个神经元都只有一个输出，且该输出仅与本神经元的输入及连接权值有关，而与其他神经元无关，因此可以对单层感知器进行简化，仅考虑只有单个输出节点的单个感知器。事实上，最原始的单层感知器模型只有一个输出节点，即相当于单个神经元。

使用感知器的主要目的是为了对外部输入进行分类。罗森布拉特已经证明，如果外部输入是线性可分的（指存在一个超平面可以将它们分开），则单层感知器一定能够把它划分为两类。^[2]设单层感知器有n个输入，m个输出，则其判别超平面由式（8－1）确定

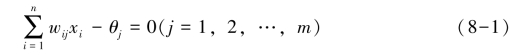
另外，需要指出的是，单层感知器可以很好地实现“与”“或”“非”运算，但却不能解决“异或”问题。

（二）多层感知器(www.xing528.com)

多层感知器是通过在单层感知器的输入层、输出层之间加入一层或多层处理单元所构成的。其拓扑结构与多层前馈网络相似，区别仅在于其计算节点的连接权值是可变的。

多层感知器的输入层与输出层之间是一种高度非线性的映射关系，如多层前馈网络（见图8－2）。若采用多层感知器模型，则该网络就是一个从n维欧氏空间到m维欧氏空间的非线性映射。因此，多层感知器可以实现非线性可分问题的分类。例如，对“异或”运算，用如图8－3所示的多层感知器即可解决。

图8-2　多层前馈网络结构

图8-3　“异或”问题的多层感知器

在图8－3中，隐含层神经元x11所确定的直线方程为1×x1＋1×x2－0.5＝0，可以识别一个半平面。隐含层神经元x12所确定的直线方程为1×x1＋1×x2－1.5＝0，也可以识别一个半平面。输出层神经元所确定的直线方程为1×x11＋1×x12－1.5＝0，相当于对隐含层神经元x11和x12的输出进行“逻辑与”运算，因此可识别由隐含层已识别的两个半平面的交集所构成的一个凸多边形，如图8－4所示。

图8-4　“异或”问题的解决