基于上下文信息的语言建模优化策略

在任何一个真实的自然语言文本中，语言符号的出现概率是相互关联、相互制约的，只有考虑上下文之间的关系，才能真实地描述文本的本质，况且考虑的上下文信息越多，语言模型所反映的语序越逼近真实的语言句法模式。所以，这类语言模型也是近年来语言模型研究的重点，它在机器翻译、语音识别、文本校对等领域具有十分重要的应用价值。这类语言模型的建立，主要依据随机过程理论或信息论理论建立模型的数学结构，再通过统计方法和语句中的上下文信息实现模型参数的整定。

（一）基于随机过程理论的模型构造

自然语言文本中各语言符号的出现概率并不相互独立，每个随机试验的结局依赖于它前面的随机试验的结局，也就是说，各语言符号的出现是相互联系相互制约的，它表明可以将自然语言文本看作一个随机过程。

基于随机过程原理所建立的自然语言模型必能更加准确反映语言的本质，n－gram模型和隐马尔科夫模型（HMM）多年来在自然语言处理领域长盛不衰的原因可能就在于此。因为n－gram模型和HMM实际上都是基于随机过程原理而建立的语言模型。

1.n－gram模型与Markov模型

Markov模型是独立随机试验模型的直接推广，它因早在1906年俄国著名数学家马尔科夫（Markov）对其研究而得名。Markov模型指出，对一个随机过程{Xn，n≥0}，如果i0，i1，…，in－1，i，j是一组不同的状态，它满足无后效性条件：

则该随机过程Xn为离散时间的Markov链。

随机过程有两层含义：第一，它是一个时间函数，随时间的改变而改变；第二，每个时刻上的函数值是不确定的，是按照一定的概率随机分布的。实际上，自然语言中每个字母或音素的出现随着时间的改变而改变，是时间的函数，而在每个时刻上出现什么字母（或音素）则有一定的概率性，是随机的。1913年，Markov就注意到语言符号出现概率的相互影响，指出自然语言就是一个由有记忆信源发出的Markov链，在这一Markov链中，前面的语言符号对后面的语言符号是有影响的。

如果只考虑前面一个语言符号对后面一个语言符号出现概率的影响，这样得出的语言成分的链称作一阶马尔科夫链；如果考虑前面两个语言符号对后面一个语言符号出现概率的影响，则称作二阶马尔科夫链，以此类推，当考虑前面n个语言符号对后面一个语言符号出现概率的影响，则称作n阶马尔科夫链。随着马尔科夫链阶数的增大，随机试验所得出的语言符号链愈来愈接近有意义的语言文本。然而，正像语言学家乔姆斯基所指出的，描述自然语言的马尔科夫链的阶数并不是无穷增加的，它的极限就是语法上和语义上成立的自然语言句子的集合，这样，就有理由将自然语言的句子看成是重数很大的马尔科夫链了。^[6]

n－gram模型是近年来最流行的语言模型，它是这样定义的：如果用变量S代表文本中一个任意的符号（字、词、词性标记或义类标记符号）序列，它由顺序排列的n个符号组成，即S＝W1W2…Wi…Wn则S在文本中的出现概率P（W1W2…Wi…Wn ）可以用下式表示：

其中，P（Wn/W1W2···Wn－1）表示在给定上下文信息W1W2···Wn－1的条件下，Wn的出现的概率，即要考虑前面的n－1个符号对当前符号出现情况的影响。这种模型由于假设当前词的出现只与前面n－1个词有关，而与其他词无关，可以看作满足Markov模型的无后效性条件，也就可以将其看作是一个广义的n－1阶Markov模型。

2.隐Markov模型

隐Markov模型是由鲍姆（Baum）首先提出的，后被广泛地应用于语音识别和词性标注。它包含了双重随机过程，一个是系统状态变化的过程，状态变化所形成的状态序列叫作状态链；另一个是由状态决定观察的随机过程，是一个输出的过程，所得到的输出序列称作输出链。“隐”的意思就是输出链是可观察到的，但状态链却是“隐藏”的、看不见的。一个隐Markov模型的形式描述为λ＝（A，B，π），其中，A＝{aij}为状态转移概率矩阵，且0≤aij≤1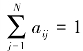，，aij表示从状态i转移到状态j的概率；B＝{bij （K）}为输出概率矩阵，且0≤bij≤1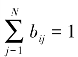，，bij （K）表示从状态i转移到状态j时输出为K的概率；π为系统的初始概率分布。

3.与基于概率分布的统计模型区别

由于考虑相邻词间的相互影响，基于随机过程理论所构造的语言模型中包含了相邻词间的转移概率，所以，Markov和隐Markov模型中的一个很重要的参数就是状态转移矩阵，而在基于概率分布的统计模型中不会涉及词间的转移概率问题。

4.建模时要考虑的因素

在构造n－gram模型时，主要涉及以下问题：

（1）模型参数n的选取。从理论上讲，n值越大，所反映的语序越逼近真实的句法模式，因而会有更加良好的语法匹配效果。但在实际应用中，n值的增大又会带来存储资源的急剧扩张和因统计数据稀疏而造成的计算误差。

（2）建模单元的选择。选择合适的建模单元，对模型的性能也有非常大的影响。例如，在对汉语语言建立模型时，可以字为单位建立模型，也可以词为单位建立模型。当n相同时，基于词的模型优于基于字的模型，当然构造的难度也大，这是由于汉语中词的数量远多于字的数量。所以，要提高所建模型的性能，阶数n与建模单元的选择是需要权衡的一对矛盾。

（3）信道模型的选择。不同的信道模型适合于不同的应用对象，也可能导致不同的模型结构。

（4）状态转移矩阵的求取。这要通过对语料的统计处理才能得到。(www.xing528.com)

在构建隐Markov模型时，首先是确定系统状态，并为系统的初始状态赋初值，形成系统的初始概率分布；然后，根据系统状态的数量以及语料统计数据获取状态转移矩阵以及输出概率矩阵，关键之处是参数的求取。

（二）基于信息论最大熵方法的模型构造

最大熵方法是根据上下文建立语言模型的一种有效方法，它以上下文中对当前词的输出有影响的信息为特征，以信息论为理论依据，计算这些特征的信息熵，信息熵最大的特征说明对当前词的表征作用最强，并以这些特征构造模型。其问题描述如下：

设随机过程P所有的输出值构成有限集Y，对于每个输出y∈Y，其生成均受上下文信息x的影响和约束。已知与y有关的所有上下文信息组成的集合为X，则模型的目标是：给定上下文x∈X，计算输出为y∈Y的条件概率，即对进行估计。表示在上下文为x时，模型输出为y的条件概率。

由问题的描述可知，基于最大熵的建模方法涉及以下因素。

1.特征

随机过程的输出与上下文信息工有关，但在建立语言模型时，如果考虑所有与y同现的上下文信息，则建立的语言模型会很烦琐，而且从语言学的知识上来讲，也不可能所有的上下文信息都与输出有关。所以在构造模型时，只要从上下文信息中选出与输出相关的信息即可，称这些对输出有用的信息为特征。

2.特征的约束

与输出对象有关的上下文信息特征集合可能很大，但真正对模型有用的特征只是它的一个子集，因此，根据模型的要求对特征候选集中的特征进行约束。

3.模型的构造和选择

利用符合要求的特征所构造的模型可能有很多个，而模型的目标是产生在约束集下具有最均匀分布的模型，而条件嫡则是均匀分布的一种测量工具。最大熵的原理就是选择其中的一个条件熵最大的模型作为最后所构造的模型。

从上面的论述可知，基于上下文的语言模型主要依据随机过程的理论而建造，之所以应用n－gram模型和隐Markov模型，就是假设自然语言为具有Markov性的随机过程。那么，可否用Poison过程或Brown运动来刻画自然语言呢？如果可以的话，是否就可建立具有新的结构的语言模型呢？当然也可以应用别的类似于最大熵的方法来构造语言模型。事实上，已有人将Poisson模型应用于文本检索，也有人尝试过Brown模型的应用。我们提出这些问题，就是为了能够开阔人们的语言建模思路。

【注释】

[1]蒋晓丽，赵毅衡.传播符号学访谈录新媒体语境下的对话[M].成都：四川大学出版社，2017：26.

[2]朱福喜，杜友福，夏定纯.人工智能引论[M].武汉：武汉大学出版社，2006：242.

[3]米爱中，姜国权，霍占强.人工智能及其应用[M].长春：吉林大学出版社，2014：247.

[4]史忠植，王文杰.人工智能[M].北京：国防工业出版社，2007：294.

[5]陈万米，汪镭，徐萍，司呈勇.人工智能源自、挑战、服务人类[M].上海：上海科学普及出版社，2018：148.

[6]张仰森.人工智能原理与应用[M].北京：高等教育出版社，2004：274.