启发式OR图搜索算法详解

大多数前向推理问题可以表示为OR图，其中图中的节点表示问题的状态，弧表示应用于当前状态的规则，该规则引起状态的转换。当有多个规则可用于当前状态的时候，可以从该状态的各个子状态中选择一个比较好的状态作为下一个状态。

（一）爬山算法

爬山算法是一种局部择优的方法，是采用启发式方法，对深度优先搜索的一种改进。^[3]“生成与测试”搜索只是扩展搜索空间，并且在该空间中检测目标是否出现。这种方法几乎是一种耗尽式搜索，效率很低。于是人们考虑是否可以利用反馈信息以帮助决定生成什么样的解，这就是爬山算法。爬山算法采用了前面定义的评估函数f（x）用来估计目标状态和当前状态的“距离”。当一个节点被扩展以后，对节点x进行评估得到f（x），按f（x）的升序排列这些函数值，并把这些节点按f（x）的升序压入栈。所以，栈顶元素具有最小的f（x）值。现在弹出栈顶元素并和目标节点比较，如果栈顶元素不是目标，则扩展栈顶元素，并计算其所有子节点的f值，并按升序把这些子节点压入栈中。如果栈顶元素是目标，则算法退出，否则该过程会循环下去，直到栈为空。下面给出它的搜索过程：

爬山算法一般存在以下三个问题。

（1）局部最大：由于爬山算法每次选择f值最小的节点时都是从子节点范围内选择，选择范围较窄。因此爬山算法是一种局部择优的方法。局部最大一般比状态空间中全局最大要小，一旦到达了局部最大，算法就会停止，即便该答案可能并不能让人满意。

（2）高地：高地是状态空间中评估函数值基本不变的一个区域，也称为平顶，在某一局部点周围f（x）为常量。一旦搜索到达了一个高地，搜索就无法确定要搜索的最佳方向，会产生随机走动，这使得搜索效率降低。

（3）山脊：山脊可能具有陡峭的斜面，所以搜索可以比较容易地到达山脊的顶部，但是山脊的顶部到山峰之间可能倾斜得很平缓。除非正好有合适的操作符直接沿着山脊的顶部移动，否则该搜索可能会在山脊的两面来回震荡，搜索的前进步伐会很小。

在每种情况中，算法都会到达一个点，使得算法无法继续前进。如果出现这种情况，可以从另外一个点重新启动该算法。这称为随机重启爬山算法。爬山算法是否成功和状态空间“表面”的形状有很大的关系：如果只有很少的局部最大值，随机重扁爬山算法将会很快地找到一个比较好的解答。如果该问题是NP完全的，则该算法不可能好于指数时间。这是因为一定具有指数数量的局部最大值。然而，通常经过比较少的步骤，爬山算法一般就可以得到比较合理的解答。

（二）模拟退火法

“退火（Annealing）”是金属铸造的一个过程，它是指金属首先在高温下熔化，然后让它冷却下来直到它成为固态。^[4]因此，在退火的物理过程中，温度很高的材料的能量逐渐丢失，最终达到最小能量的状态。一般情况下，大多数物理过程是从高温状态转换到低温状态，但是仍然有比较小的概率，它可以跨越能量状态的低谷，上升到另一个能量状态。例如，考虑一个滚动的球，从一个高能量状态滚动到一个低谷，然后滚到高一点的能量状态（见图4－5）。然而滚动到高能量状态的概率非常小，一般为：

图4-5　滚动的球从低谷到稍高一点的能量状态

其中p是从低能量状态转换到高能量状态的概率，ΔE表示能量正的改变，K是Boltzman常量，T是当前状态的温度。对于很小的ΔE，p的值比ΔE很大时的p的值要大。这样自然就会有一个问题：如何在搜索中实现退火？在这个阶段，应该记住：模拟退火算法是在函数，产生了没有比当前状态更好的下一个状态时，用来指出搜索方向的。这时，对所有可能的下一个合理状态计算ΔE的值，并用下式计算p’的值：

在闭区间[0，1]中随机得到一个数字，然后和p’比较。如果p’大，则选择它作为下一个转换状态。参数T在搜索程序中是逐渐降低的。这时由于T降低，p’也降低，从而使得算法终止在一个稳定的状态。模拟退火算法可表示如下。

如果总是存在一个比现在状态更好的下一个状态，并且该状态就是栈顶指针指向的状态，则该算法和爬山算法类似。如果不是这种情况，则会调用算法最后的Begin－End部分。这一部分就是模拟退火部分。它一个一个检测合理的后续状态，查看该状态出现的概率是否大于[0，1]之间的随机值。如果是，则选择该状态，否则检测下一个可能的状态。我们希望的是至少有一个状态出现的概率大予随机生成的概率。

需要说明的是，算法中没有包括ΔE的计算。它是取下一个可能状态的能量值和当前状态能量值的差。另一个问题是一旦选择了希望比较小的新的状态时，T应该是下降的。T总是非负的。当T为零时，p’也会为零，这样转换到其他状态的概率都为零。

（三）最好优先

以上讨论的各种算法，主要问题是如何选择下一个状态来考察。爬山算法是按希望的大小来排列初始状态，然后检测位于列表中第一个位置的状态。如果它是目标，算法终止；如果它不是目标，该状态由其儿女替代，这些儿女以某种顺序放入列表的前面。因此爬山算法还是没有脱离深度优先法的基本思想。而在最好优先方法中，搜索是从最有希望的节点开始，并且生成其所有的儿女节点。然后计算每个节点的性能（合适性），基于该性髓选择最有希望的节点扩展。(https://www.xing528.com)

注意，这里是对所有的节点进行检测，然后选择最有希望的节点进行扩展，而不是仅仅从当前节点所生成的子节点中进行选择。因此和爬山算法不同，如果在早期选择了一个错误的节点，最好优先搜索提供了一个修改的余地。这是最好优先搜索和爬山算法相比比较好的一点。

最好优先搜索算法是一个通用的算法，但是，该算法并没有显式地给出如何定义启发式函数，并且它不能保证当从起始节点到目标节点的最短路径存在时，一定能够找到它。为此需要对启发式函数等进行限制，A*算法就是对启发式函数等问题加上限制后得到的一种启发式搜索算法。

（四）通用图搜索算法

图搜索算法只记录状态空间中那些被搜索过的状态，它们组成一个搜索图称为G。G由两种节点组成：

定义4－1：一个节点称为Open，如果该节点已经生成，而且启发式函数值h （x）已经计算出来，但是它还没有扩展。这些节点也称为未考察节点。

定义4－2：一个节点称为Closed，如果该节点已经扩展并生成了其子女。Closed节点是已经考察过的节点。

因此可以给出两个数据结构OPEN和CLOSED表，分别存放Open节点和Closed节点。

根据前面的讨论，节点x总的费用函数，（x）是g（x）和h（x）之和。生成费用g（x）可以比较容易地得到，例如，如果节点x是从初始节点经过m步得到，则g（x）应该和m成正比（或者就是m）。但是如何计算h（x）呢？显然h （x）只是一个预测值，下面是图搜索算法的一个描述。

上述图搜索算法生成一个明确的图G（称为搜索图）和一个G的子集T（称为搜索树），图G中的每个节点也在树T上。搜索树是由返回指针来确定的。G中的每一个节点（除了初始节点S0外）都有一个指向G中一个父辈节点的指针。该父辈节点就是树中那个节点的唯一父辈节点。

算法中（3）（4）步保证对每一个扩展的新节点，其返回指针的指向是已产生的路径中代价最小的。这可用图4－6来说明。

图4-6　搜索图和搜索树

设搜索算法已生成如图4－6（a）所示的搜索图和搜索树（带返回指针的部分）。图中实心圆点表示在CLOSED表中的节点，空心圆点表示在OPEN表中还未扩展的节点。图4－6（a）是扩展节点1之前的搜索图和搜索树，而图4－6（b）是扩展节点1之后的搜索树和搜索图。

当节点1扩展时，产生节点2。而节点2是CLOSED表中的节点，节点2的新g（2）值为2（设相邻两节点之间的代价均为1），而原来g（2）值为4，故将节点2的指针指向节点1，将原来指向节点3的指针断开。同时要考虑修改节点2的后继节点4的返回指针和g（4）的值，将节点4指向节点2，并把原来指向节点6的指针断开。

下面再通过一个例子来说明该算法的使用问题。给定4 L和3 L的水壶各一个。水壶上没有刻度。可以向水壶中加水。如何在4 L的壶中准确地得到2 L水？

在这里用（x，y）表示4 L壶里的水有x L和3 L壶里的水有y L，n表示搜索空间中的任一节点。则给出下面的启发式函数：

假定g（n）表示搜索树中搜索的深度。则根据图搜索策略可以得到如图4－7所示的搜索空间。

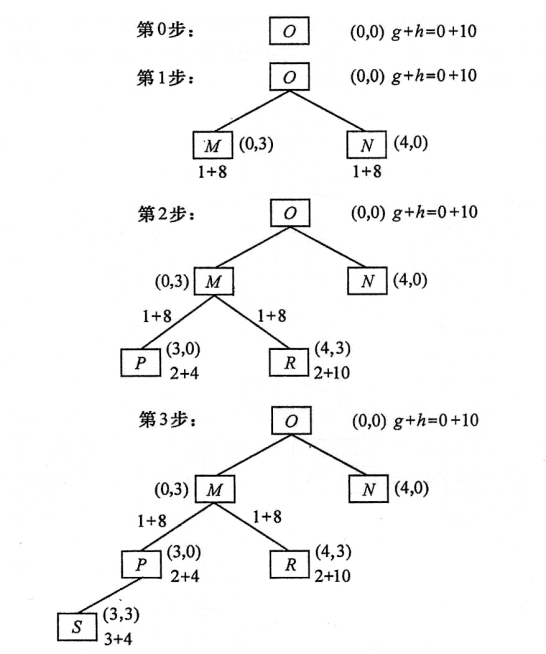
图4-7　水壶问题的状态空间扩展

在第0步，由节点O可以得到g＋h＝10。在第1步，得到两个节点M和N，其估价函数值都为1＋8＝9，因此可以任选一个节点扩展。假定选择了节点M，在第2步扩展M得到两个后继节点P和R，对于P有2＋4＝6，对于R有2＋10＝12。现在，在节点P、R、N中，节点P具有最小的估价函数值，所以选择节点P扩展。在第3步，可以得到节点S其中3＋4＝7。现在，在节点S、R、N中，节点S的估价函数值最小，所以下一步就会选择S节点扩展。该过程一直进行下去，直到到达目标节点。