深度优先搜索的时间复杂性和局限性

深度优先搜索生成节点并与目标节点进行比较是沿着树的最大深度方向进行的，只有当上次访问的节点不是目标节点，而且没有其他节点可以生成的时候，才转到上次访问节点的父节点。转移到父节点后，该算法会搜索父节点的其他的子节点。因此深度优先搜索也称为回溯搜索，它总是首先扩展树的最深层次上的某个节点，只有当搜索遇到一个死亡节点（非目标节点而且不可扩展），搜索方法才会返回并扩展浅层次的节点。上述原理对树中每一节点是递归实现的，实现该递归过程的比较简单的一种方法是采用栈。下面的方法就是基于栈实现的深度优先搜索算法：

在上述算法中，初始节点放到栈中，栈指针指向栈的最上边的元素。为了对该节点进行检测，需要从栈中弹出该节点，如果是目标，该算法结束，否则把其子节点以任何顺序压入栈中。该过程直到栈变成为空。图4－3所示是采用深度优先的方法遍历一棵树的过程。

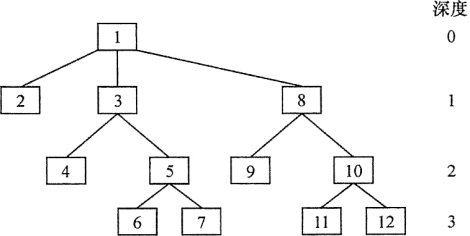
图4-3　深度优先算法对深度为3的树的遍历顺序

（一）深度优先搜索的空间复杂性

深度优先搜索对内存的需求是比较适中的。它只需要保存从根到叶的单条路径，包括在这条路径上每个节点的未扩展的兄弟节点。当搜索过程到达了最大深度的时候，所需要的内存最大。假定每个节点的分支系数为b，当我们考虑深度为d的一个节点时，保存在内存中的节点的数量包括到达深度d时所有未扩展的节点以及正在被考虑的节点。因此，在每个层次上都有（b－l）个未扩展的节点，总的内存需要量为d（b－1）＋1。因此深度优先搜索的空间复杂度是b的线性函数O（bd），而宽度优先搜索的空间复杂度是b的指数函数。事实上，这也是深度优先搜索最有用的一个方面。(www.xing528.com)

（二）深度优先搜索的时间复杂性

如果搜索在d层最左边的位置找到了目标，则检查的节点数为（d＋l）。另一方面，如果只是搜索到d层，而在d层的最右边找到了目标，则检查的节点包括了树中所有的节点，其数量为：

所以，平均来说，检查的节点数量为：

上式就是深度优先搜索的平均时间复杂度。

深度优先搜索的优点是比宽度优先搜索算法需要较少的空间，该算法只需保存搜索树的一部分，它由当前正在搜索的路径和该路径上还没有完全展开的节点标志所组成。因此，深度优先搜索的存储器要求是深度约束的线性函数。但是其主要问题是可能搜索到了错误的路径上。很多问题可能具有很深甚至是无限的搜索树，如果不幸选择了一个错误的路径，则深度优先搜索会一直搜索下去，而不会回到正确的路径上。这样对于这些问题，深度优先搜索要么陷入无限的循环而不能给出一个答案，要么最后找到一个答案，但路径很长而且不是最优的答案。这就是说深度优先搜索既不是完备的，也不是最优的。