人类的思维过程和推理活动在本质上是非单调的。人们对客观事物的认识和信念总是不断调整和深化的,于是出现了上述认识上的非单调性。在这种情况下,推导出的结论不随条件的增加而增多。这种推理过程就是非单调推理。
非单调推理的概念是明斯基(Minsky)于1975年提出来的,并以“鸟会飞”为例加以说明。人们常识上认为大多数鸟会飞。当知道X是鸟类中的一只鸟时,一般认为X会飞;但进一步知道X是鸟类中的一只企鹅时,因为企鹅不会飞,所以需要对“鸟会飞”的结论加以修正。
非单调推理具有下列特性:推理系统的定理集合不随推理过程的进行而单调增大,新推理出的定理很可能会修正以至否定原有的一些定理,使得原来能够解释的一些现象变得不能解释了。
非单调推理是人工智能非常活跃的研究领域,有代表性的研究工作有赖特(Reiter)的缺省推理、穆尔(Moore)的自认识逻辑、麦卡锡(MeCarthy)的界限推理和多伊尔(Doyle)的真值维护系统等。下面笔者主要介绍缺省推理与真值维护系统。
(一)缺省推理
1.缺省推理的定义
很少有这样完美的信息系统——其在处理过程中拥有所需的一切信息。在缺乏信息时,一个有效的做法就是根据已有信息和经验做有益的猜测,只要不发现反面的证据。构造这些猜测的过程称为缺省推理。[6]
一个既精确又可算的缺省推理的描述,必涉及结论Y且缺少某一信息X。所以缺省推理的一个定义为:
定义3-8:如果X不知道,那么得结论Y。
但在所有的系统中,除最简单的系统以外,只有存储在数据库中的事件的极小部分可看成是已知的。不过,通过各种努力,事件的其余部分可从已知部分推导出来。所以缺省推理的另一定义更像是:
定义3-9:如果X不能被证明,那么得结论Y。
但是,如果仍然以谓词逻辑工作,那怎么能知道X不能被证明┐由于这一系统是不可判定的,所以对任一X来说,仍不能担保它能否被证明。于是不得不重新考虑下述定义:
定义3-10:如果X不能在某个给定的时间内被证明,那么得结论Y。
值得注意的是,定义推出结论Y的推理过程依赖于逻辑领域以外的某些事件,在规定时间内可做多少计算,以及在寻找待求的证明中计算是否有效。因此做出关于系统行为的形式说明就显得特别重要。
2.缺省推理的规则表示
根据赖特的缺省理论,其缺省推理的规则的表达式为
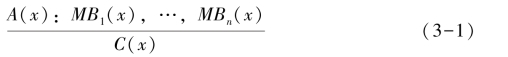
其中,A(x),Bi(x),C(x)分别叫作缺省规则的先决条件、默认条件及结论(i=1,2,…,n),它们都是自由变元x的合式公式;M称为模态算子,表示“假定……是相容的”,即其否定不可证明。
式(3-1)的缺省规则表示:如果先决条件A(x)成立,而且假定默认条件Bi(x)(i=1,2,…,n)相容,即没有证据证明Bi(x)不成立,则可推出结论C(x)成立。
另外,需要说明的是,缺省规则虽然可以表示模糊量词“几乎”“大多数”等,但它却不涉及模糊逻辑。
3.缺省规则的分类
按规范式表示形式可把缺省规则分为规范缺省、半规范缺省及非规范缺省三类。
(1)规范缺省规则
若默认条件为B(x),且有
![]()
则称这样的缺省规则为规范缺省规则。
对规范缺省规则,可表示为

其含义是:由先决条件A(x)成立一般可推出结论B(x)成立。例如,对如下知识:
一般来说,大学生都掌握英语
可用缺省规则表示为
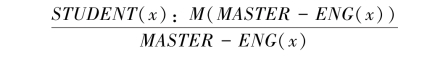
(2)半规范缺省规则
若默认条件为B(x),且有
![]() (https://www.xing528.com)
(https://www.xing528.com)
则称这样的缺省规则为半规范缺省规则。
对于半规范缺省规则,可表示为
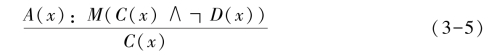
其含义是:除D(x)外,由先决条件A(x)的成立一般可推出结论C(x)成立。例如,对如下知识:
![]()
可用缺省规则表示为
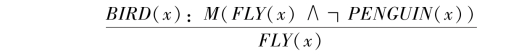
(3)不规范缺省规则
凡是不属于前两类的缺省规则都称为不规范缺省规则。
此外,如果在缺省规则中不含自由变元,则称该缺省为封闭的;如果先决条件为空,为重言式;如果默认条件为空,则退化为演绎规则。
缺省理论在处理很多智能问题中都起着重要的作用,尤其是对于解决常识性推理更显得重要。此外,由于缺省推理所得到的往往只是一种信念,而人们对世界的认识可以有几种不同的信念且可以改变,因此允许对同一事物分别得到不同信念的缺省规则同时存在。
缺省理论也存在着一些困难问题。例如,当增加一条新的缺省规则时,有时会因为缺省规则间的相互作用而出现一些不应有的结果。尽管赖特曾提出建立一个完整性维持系统作为辅助系统,用来检测缺省规则间潜在的相互作用,并对有关缺省规则进行重新表示,然而这项工作是很复杂的。这就给缺省理论的实际应用带来了困难。
(二)真值维护系统
维持推理的一致性是实现非单调推理系统的核心技术之一。可以把一个非单调推理系统的信念集(常识集)分为两个部分,即S=Δ∪A。其中,Δ为基本信念集;A为假设集,可视为对Δ的尝试性扩充。鉴于推理系统视Δ为永真,因而推理中产生的不一致仅由引入不适当的假设引起。尽管已对确保A与Δ的一致性做了许多探索,但大多数非单调推理方法仅适用于特别的应用场合,尚不存在适用于一般应用域的简便方法。现有的实用化非单调推理系统,主要依赖于应用的特点和有关知识,提出不保证与Δ一致的试探性假设(实际上Δ往往也是问题求解过程中逐步积累起来的,即使用形式化方法也不可能确保提出的假设不与以后加入Δ的信念冲突)。真值维持系统(truth maintenance system,TMS)正是服务于维持推理一致性的有效技术。
TMS最早由多伊尔于1979年建立。TMS的作用在于协助问题求解系统维持推理过程的正确性,而不是自身产生新的推理。一个非单调推理系统应由两个部分组成:问题求解器和TMS。前者基于应用领域的知识进行推理和计算,后者则通过真值维持确保推理上下文的一致性。实际上,可视TMS为从属于问题求解器的子系统,它执行两个主要功能:检查推理上下文的一致性;消除发现的不一致性。
真值维持系统运用非单调推理的思想和技术来维护知识库。在TMS中,每个知识单元都是一个信念,每个信念都有其正面或反面的论据。在推理过程中论据发生了变化,信念也随之发生变化。TMS的作用原理如图3-1所示。

图3-1 真值维持系统
从上述讨论可以看出,TMS是一个已经实现了的非单调推理系统,用以协助其他推理程序维持系统的正确性。它的作用不是生成新的推理,而是在其他程序所产生的命题之间保持相容性。一旦发现某个命题不相容,它就调出自己的推理机制,面向从属关系的回溯,并通过修改最小的信念集来消除不相容。
从上述讨论可以看出,TMS是一个已经实现了的非单调推理系统,用以协助其他推理程序维持系统的正确性。它的作用不是生成新的推理,而是在其他程序所产生的命题之间保持相容性。一旦发现某个命题不相容,它就调出自己的推理机制,面向从属关系的回溯,并通过修改最小的信念集来消除不相容。
在TMS中,每一命题或规则均称为节点,且对任一节点,以下两种状态必居其一:
IN 相信为真
OUT 不相信为真,或无理由相信为真,或当前没有可相信的理由
每个节点附有一证实表,表中每一项表示一种确定节点有效性的方法。IN节点是指那些至少有一个在当前说来是有效证实的节点。OUT节点则指那些当前无任何有效证实的节点。也许有人想知道为什么要不厌其烦地保留OUT节点。当然,花许多功夫去产生一些表示不正确命题的节点是没有意义的。但必须记住,在非单调推理系统中,产生一节点是以表示一个假定为真的命题,例如,使用缺省推理的结果。这时其余节点则在假设原始节点为IN的基础上产生。但新信息的出现可能引起原始节点变成OUT(缺少信息时用缺省推理),那时,一切基于它的节点都相应要变为OUT。不过,保留这些节点和它们的相互依赖性仍有用处。因为一旦有效信息发生了变化,而且引起原始节点再变为IN时,那些在其基础上用来产生其他节点的推理就不必重做了。于是,当原始节点再变为IN时,其他各个节点的某个基于原始节点的证实将随之变为有效,这些节点也就变为IN了。
在系统中,有两种方式可用来证实一个节点的有效性可依赖于其他节点的有效性:
(1)支持表 (SL(IN-节点)(OUT-节点))
(2)条件证明 (CP(结论)(IN-假设)(OUT-假设))
【注释】
[1]邓朝晖,万林林,邓辉,张晓红,刘伟.智能制造技术基础[M].武汉:华中科技大学出版社,2017:55.
[2]郝博,胡玉兰,赵岐刚.智能设计[M].沈阳:辽宁科学技术出版社,2013:98.
[3]史忠植,王文杰.人工智能[M].北京:国防工业出版社,2007:119.
[4]郝博,胡玉兰,赵岐刚.智能设计[M].沈阳:辽宁科学技术出版社,2013:100.
[5]雷英杰.模糊逻辑与智能系统[M].西安:西安电子科技大学出版社,2016:87.
[6]高济.人工智能基础[M].北京:高等教育出版社,2002:291.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




