模糊推理基础及基本模式

（一）模糊推理的概念

传统的逻辑推理是基于二值逻辑的，它所处理的信息和推理的规则是精确和完备的。与此对应，还有一种不精确推理，也称为不确定性推理或近似推理，它利用不精确、不完备的知识处理不精确、不确定、不完备信息。

模糊逻辑推理是建立在模糊逻辑基础上的，它是在二值逻辑三段论基础上发展起来的一种不确定性推理方法，可简称为模糊推理。^[5]这种推理方法以模糊判断为前提，运用模糊语言规则，推导出一个近似的模糊判断结论的方法。

（二）模糊理论

1.模糊集合及其表示

在德国数学家康托（G.Contor）创立的经典集合论中，一个事物要么属于某集合，要么不属于某集合，二者必居其一，没有模棱两可的情况。这表明，经典集合所表达概念的内涵和外延都必须是明确的。

概念的内涵是指一个概念所包含的那些区别于其他概念的全体本质属性。概念的外延是符合某概念的对象的全体。表达一个概念通常有两种方法，一是指出概念的内涵即内涵法，另一种是指出概念的外延即外延法。实际上概念的形成总是要联系到集合论，从集合论的角度看，内涵就是集合的定义，外延则是组成该集合的所有元素。由此不难看出，内涵和外延是描述概念的两个方面。

在实际生活中，有许多没有明确外延的概念，称之为模糊概念。表现在语言上有许多模糊概念的词，如以人的年龄为论域，那么“年轻”“中年”“老年”都没有明确的外延，以人的身高为论域，“高个”“矮个”也没有明确的外延。这些概念都是模糊概念。

模糊概念不能用经典集合描述，因为不能绝对地区别“属于”或“不属于”，就是说论域上的元素符合概念的程度不是绝对的1或0，而是介于1和0之间的一个实数。模糊概念需要用模糊集合描述，扎德在1965年给出了模糊集合的定义。

定义3－5：（模糊集合）设给定论域U，U到[0，1]闭区间的任一影射μA

都确定U的一个模糊集合A，μA称为模糊集合的隶属函数，μA（u）称为u对于A的隶属度。

上述定义表明，论域U上的模糊集合A由隶属函数μA，来表征，μA的取值范围为闭区间[0，1]，从μA（u）的大小反映了u对于模糊集合A的从属程度。μA（u）的值接近于1，表示u从属A的程度很高；μA（u）的值接近于0，表示u从属A的程度很低。可见，模糊集合完全由其隶属的数描述。

当μA的值域为{0，1}时，μA蜕化成经典集合的特征函数，模糊集合A蜕化成经典集合。即经典集合是模糊集合的特殊形态，模糊集合是经典集合概念的推广。

当论域为离散有限集，即当论域U＝{u1，u2，…，un}时，模糊集可用

表示，A中μA（u）的顺序必须与U中u的顺序相同，ui的隶属度μA（ui）为0时也必须写上，以保证A与U中的元素个数相同，顺序相同。

扎德（Zadeh）为了具体指出论域元素与其隶属度的对应关系，定义了如下的表示方法：

式中，μA（ui）/ui不是相除关系，只是说明μA（ui）是u对模糊集A的隶属度；同样式中的“＋”号不是相加的意思，只是一个分隔符。若u的隶属度μA（ui）为0时，可以略去不写。

模糊集还可以用单点形式

或序偶形式表示。

表示。

例如论域U＝{1，2，3，4，5}上的模糊集A可表示为：

若论域U是连续域时，扎德给出模糊集A的表示形式为：

同样，μA（u）/u不是表示分数，只是说明μA（u）是u对模糊集A的隶属度：“∫”不是“积分”或“求和”，只是表示论域中各元素与其隶属度对应关系的一个总括。

2.模糊集合的运算

（1）模糊集合的包含和相等关系

设A，B∈F（U），若对任意u∈U，都有μB（u）≤μA（u）成立，则称集合A包含集合B，记为A⊇B。

如果A⊇B且B⊇A，则A和B相等，记为A＝B。

若A＝B，则对于所有的u∈U，都有μB（u）＝μA（u）成立。

（2）模糊集合的并、交、补运算(www.xing528.com)

设A，B∈F（U），规定A∪B，A∩B分别表示集合A与B的并集和交集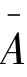，表示A的补集或余集，它们的隶属函数分别为：

模糊集合论中常用“∨”表示max，用“∧”表示min，分别表示取大、取小运算，因此并集和交集的隶属函数常写为：

3.模糊数

模糊理论中用模糊数表示模糊数量，并规定了模糊数的各种运算。

定义3－6：（凸模糊集）设A为以实数R为论域的模糊集合，即A∈F（R），若对任意实数a＜x＜b，都有

则称A为凸模糊集。

定义3－7：（模糊数）如果实数域R上的模糊集合A的隶属函数μA（u）在R上连续且具有如下性质：

（1）A是凸模糊集；

（2）A是正规模糊集，即存在u∈R，使μA（u）＝1，则称A为一个模糊数。

直观上，模糊数的隶属函数是单峰的，且在峰顶使隶属度达到1。

（三）模糊推理的基本模式

与自然演绎推理相对应，模糊推理也有相应的三种基本模式，即模糊假言推理、模糊拒取式推理及模糊假言三段论推理。

1.模糊假言推理

设F和G分别是U和V上的两个模糊集，且有知识

若有U上的一个模糊集F′，且F可以和F′匹配，则可以推出“y is G′”，且G′是V上的一个模糊集。这种推理模式称为模糊假言推理，其表示形式为

在这种推理模式下，模糊知识

表示在F与G之间存在着确定的模糊关系，设此模糊关系为F′。那么，当已知的模糊事实F′可以与F匹配时，则可通过F′与F′的合成得到G′，即

式中，模糊关系R可以是Rm、Rc或Rg中的任何一种。

2.模糊拒取式推理

设F和G分别是U和V上的两个模糊集，且有知识

若有V上的一个模糊集G′，且G′可以与G的补集┐G匹配，则可以推出“x is F′”，且F′是U上的一个模糊集。这种推理模式称为模糊拒取式推理，可表示为

在这种推理模式下，模糊知识

也表示在F与G之间存在着确定的模糊关系，设此模糊关系为R。那么，当已知的模糊事实G′可以与┐G匹配时，则可通过R与G′的合成得到F，即

式中，模糊关系R可以是Rm、Rc或Rg中的任何一种。

3.模糊假言三段论推理

设F、G、H分别是U、V、W上的三个模糊集，且由知识

则可推出