褶皱机制模型优化：深入探讨褶皱形成机理

如果在板材的厚度方向上温度梯度很小，那么温度梯度机制将失效。但是材料受热膨胀可能向上或向下产生褶皱，来容纳多余的长度（见图8.9）。褶皱最热的地方发生塑形变形，而稍冷处则发生弹性变形，冷却时中心最热处产生变形而中心以外则恢复原来形状。这种情况多发生于板材比较薄，或者热导率非常高的情况下，也就是（αD/v）1/2≫s₀。

设想褶皱发生在二维方向上，图8.9第3步可以简化为图8.10。如图所示假设在褶皱顶部曲线长为l₁范围内薄板发生塑性变形，曲线l₂范围内薄板发生弹性变形。所有区域都采用弧线或者圆形来简化几何形状。由于弹性区域的变形不是永久的，冷却后恢复原来形状，弯曲角度由塑性变形区域（区域1）决定。根据图8.10几何图形，弯曲角度由下式给出：

计算α_B需要计算r₂、l₂，r₂是弹性段弧线的半径，其数值可以根据弹性段与塑性段的弯曲力矩平衡而求出。弹性段的弯曲力矩是：

与之相平衡的塑性区域的弯曲力矩M_pl源于流动阻力：

此处：

E是弹性模量；

b是薄板宽度；

s₀是薄膜厚度；

k_f（T₁）是加热区域的流动应力。

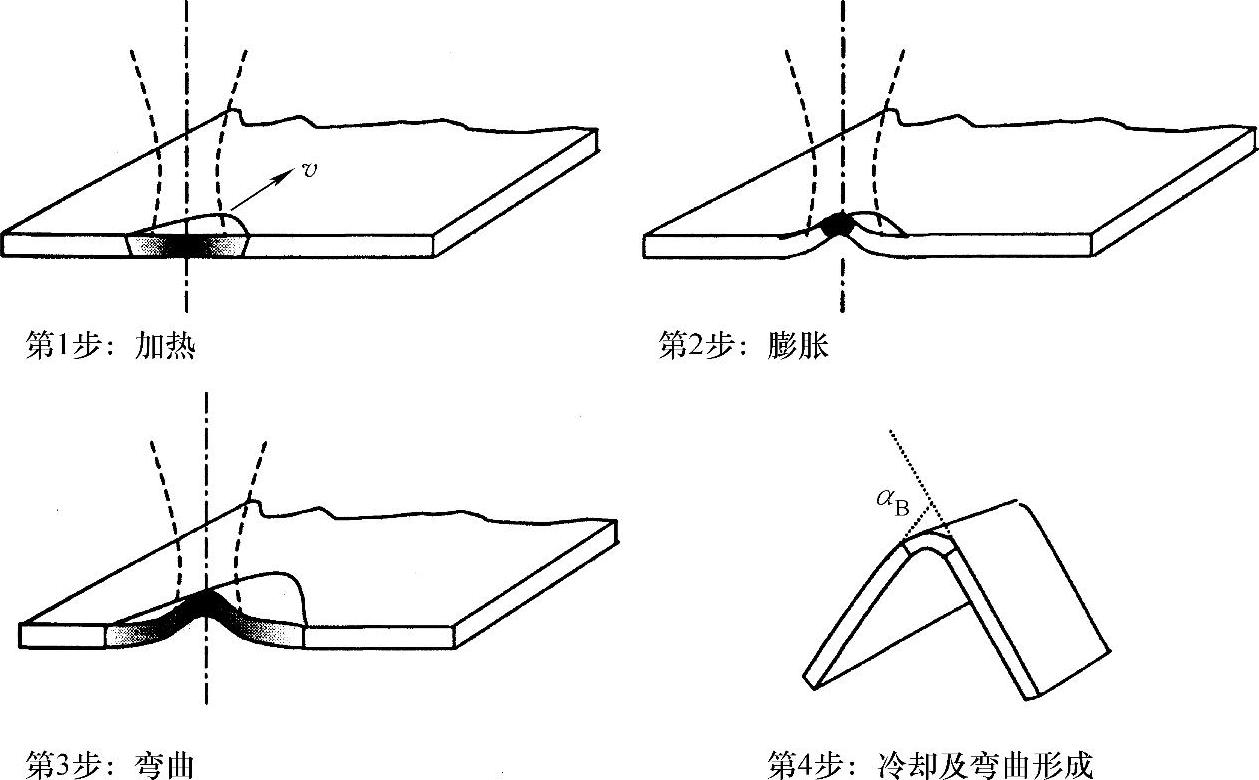
图8.9 褶皱生长步骤[7]

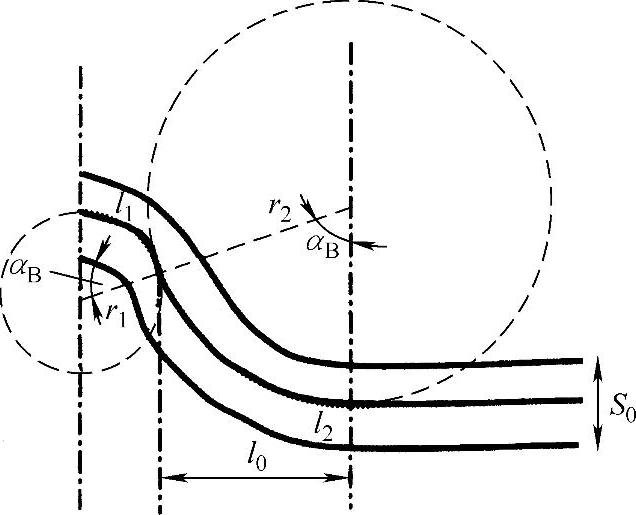
图8.10 褶皱生长步骤3的二维图

使两个力矩相等，可以解出r₂：

l₂=原始长度+区域2热膨胀

(www.xing528.com)

既然

并且

此处ΔT_av为加热区域的平均温度，加热区域可近似为长方体，长为扫描长度，宽为光斑长度，高为薄板厚度。根据热平衡可以求出平均温度：

将该式代入式（8.29）

从式（8.27），式（8.28），式（8.31）我们可以得到：

此处f′是弧线l₂段热膨胀占热膨胀总长度的百分数，取值范围为0～1，由于弧线2远大于弧线1，该值应该大，但是该区域温度低，热膨胀小，该值又应该小。任意选取一个数值如0.5，并把l₂、r₂代入式（8.23）我们得到：

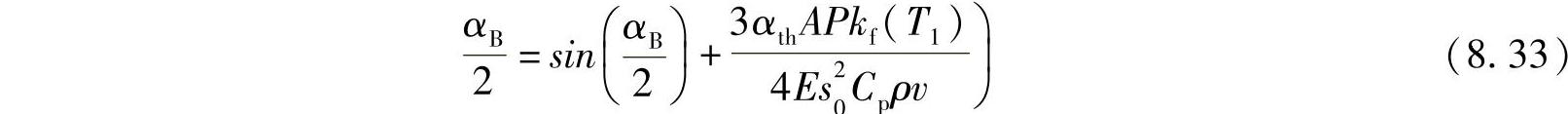
把正弦函数展开成泰勒级数，

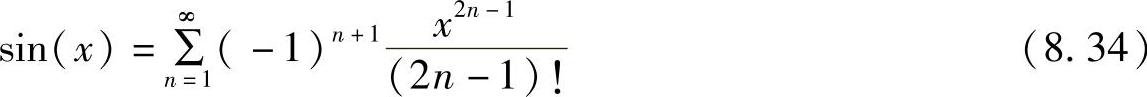
因此

假设加热区域远大于薄板厚度，褶皱机制引起的弯曲角度可以写成下式：

该式成立的条件是：板材比较薄且具有比较高的热导率，激光扫描速率比较快不会引起过热，由此R_f（T₁）较低，减小了弯曲角度。