热梯度机制模型解析

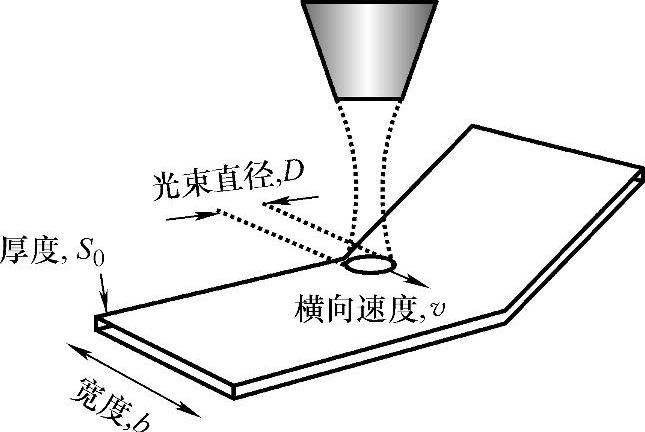
图8.4 激光线弯曲的一般装置

8.3.1.1 两层模型或者小模型

假设激光加热造成的温度场是一个阶梯函数，并且在加热层所造成的热膨胀转化为塑性流体，又假设压缩层冷却时没有应变，那么造成的弯曲可以由缩短的上半层以及下半层的长度确定，如图8.5所示。根据热平衡原理，可以得到表面层在激光辐照下温度升高的表达式：

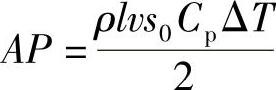
那么温度升高为：

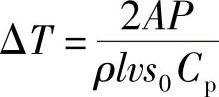
温升引起该层的热膨胀为：

从上下两个半层边线中点引直线，相交于一点，根据几何原理，可以得到弯曲角度的表达式：

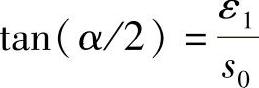
当角度很小时可以近似为：

这个关系式确定了弯曲过程的一些基本参数。比如弯曲角度与厚度的平方成反比，这与实验相符合；又比如弯曲角度线性依赖于材料的性质（α_th/ρC_p）（见图8.13）以及线能量密度（AP/v）J/m。然而该公式预言的弯曲角度远大于实验值，这归因于不是所有的热膨胀转化为塑性流体，垂直方向的温度变化也不是简单的阶梯函数。

8.3.1.2 双束模型

前面讨论的双层模型没有在弯曲板材中引入力以及力矩；另外其假设被加热层为板材厚度的一半，没有热传导。双束模型没有这些限制，但是其依然是建立在对研究对象分层基础上的，并假设被加热层被均匀加热，而底层没有被加热。加热过程中的反向弯曲能够减小加热膨胀层的压应力以及减少塑性流体以及弯曲角度，但是该模型没有计入反向弯曲的影响。

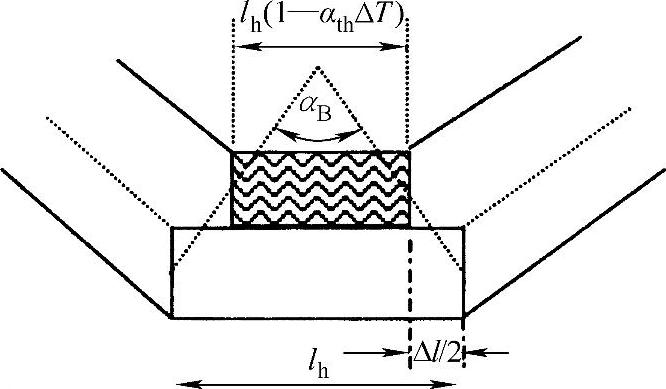
图8.5 两层模型或者小模型示意图

假设应力应变场是二维的，图8.6是弯曲薄板的应变示意图。从图中可以看出：

ε₁为加热造成总的应变，其包括扭曲力、扭曲力矩以及热膨胀：

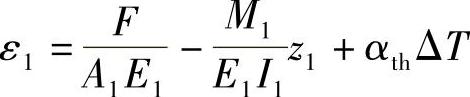
假设热膨胀造成的应变全部转化成塑性变形。那么冷却后应变为：

类似的未被加热层的应变可以表示为：

从标准力学原理可以假设：

把公式（8.5）和（8.6）代入上面公式可以得出：

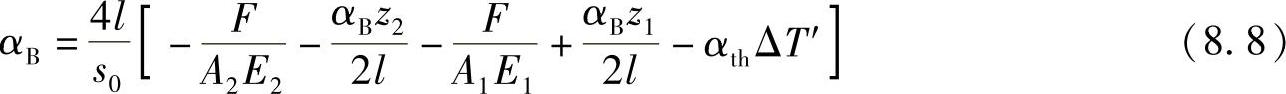
力也会导致力矩：

把z₁-z₂=s₀/2以及式（8.9）代入到式（8.8）中可以得到：

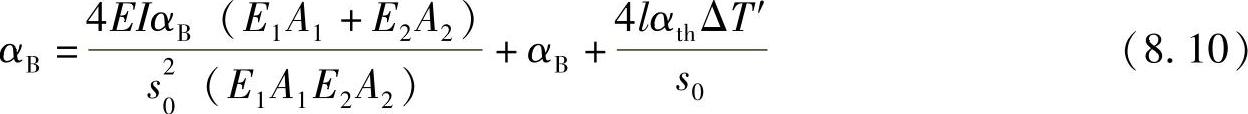
光束扫描截面定义为：

矩形光束的力矩为：

将式（8.11）与式（8.12）代入式（8.10）中，可以得到：(www.xing528.com)

根据能量守恒原理可以估计出上下两层的温度差ΔT′。输入能量为Q=0.5ΔtPA，单位面积的照射时间为Δt=D/v；D为光束直径，v为扫描速度。上层由于激光加热而引起的温升为：

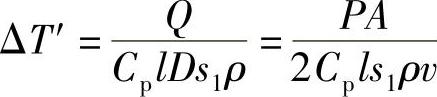
其中s₁为厚度，lDs₁ρ为上层的质量。

由于

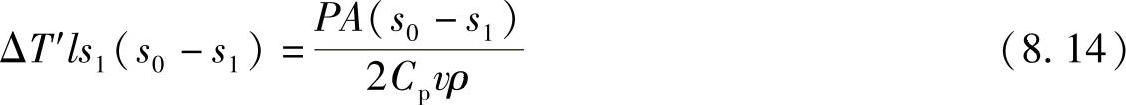
把式（8.14）代入式（8.13）得到：

当s₁=s₀/2时式（8.12）可以进一步简化为：

该式与双层模型相似，不同之处仅仅是系数不同，这里系数是3而不是4。当s₁=B（αD/v）1/2时，通过仔细选择常数B，可以使其物理意义近似为塑性变形等温线的深度。因此可以得到关于弯曲角度的公式：

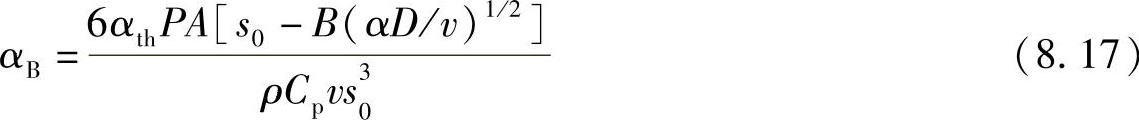
此公式有一个有趣的性质：当等温线完全贯穿时，弯曲角度为零，这可以很自然的理解为温度梯度机制失效，但褶皱机制开始发挥作用。该公式还有一个最大的速率，超过该速率，并且B取0.8弯曲角度与实验接近。式（8.17）在弯曲过程中引入了热扩散，近似地散解释了温度场。

8.3.1.3 残余应力模型

另外一个能够解释温度场的模型是Vollertsen的残余应力模型^[7]。他分别推导出两种情况的弯曲模型表达式：①表面温度还没有达到重结晶温度点，如图8.7；②表面温度达到重结晶温度点，如图8.8。该模型的基本假设是：工件一定区域如果在某个等温线之外或者该区域温度低于等温线温度T_G，则该区域不会发生塑性变形；而等温线以内区域其热膨胀被塑性流体吸收。表面温度超过重结晶温度引起的热膨胀也按重结晶温度计算。这种假设允许极热区域有一定程度的回流。模型结果总结如下：

第一种情况：表面温度低于重结晶温度，温度场部没有穿过薄板。

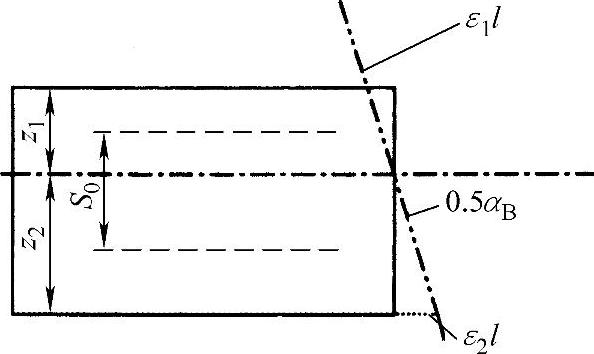
图8.6 弯曲光束造成的应变

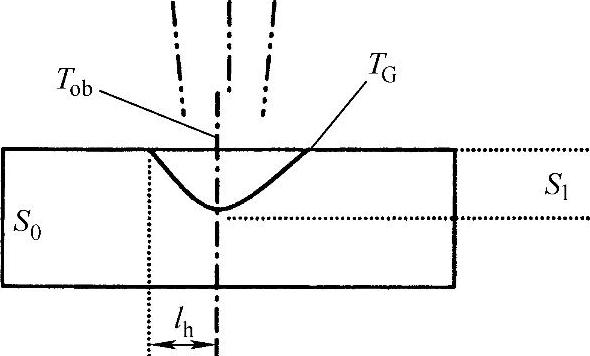
图8.7 表面温度低于重结晶温度时的弯曲模型

弯曲角度为：

表面应变为：

温度场深度为：

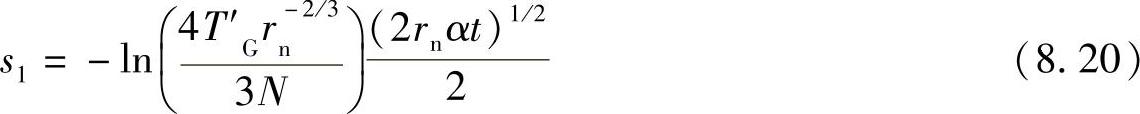
温度场的宽度为：

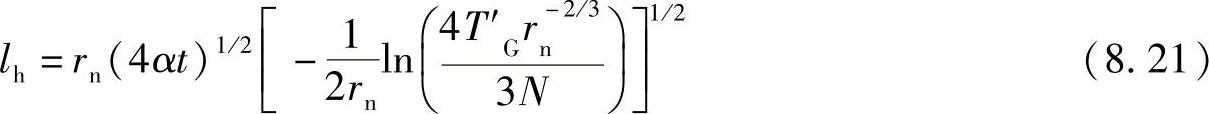
此处：

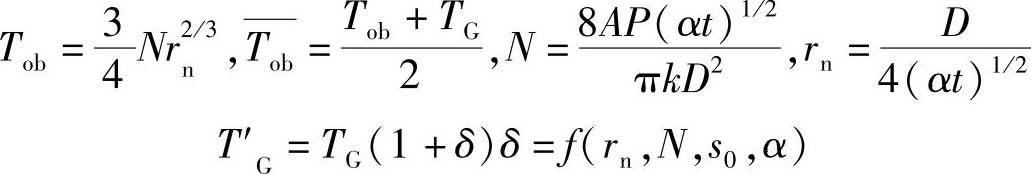
第二种情况：温度场穿透薄板，表面温度高于重结晶温度。

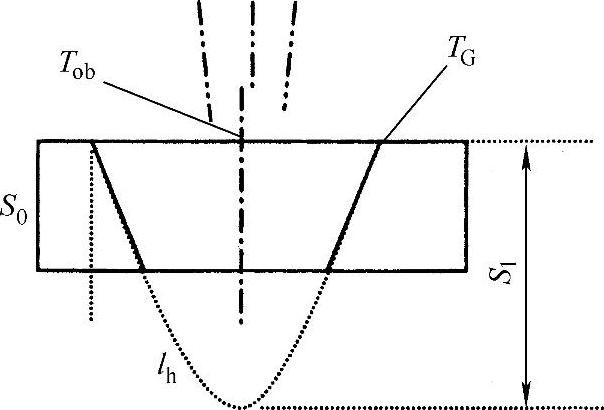
图8.8 表面温度达到重结晶温度时的弯曲模型

弯曲角度为：

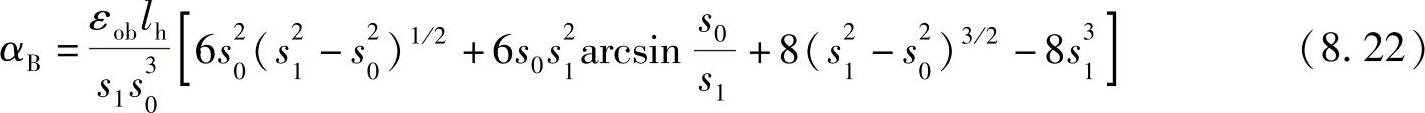
其他表达式与第一种情况相同。

这个模型做了很多简单化的假设，所得结果只具有近似意义。由于主要变量关系式由简单的模型导出，这个模型价值多于问题抑或问题多于价值还没有定论。如果要进行详细的数学分析，那么有限元方法可能是一条途径。