En24钢激光相变硬化显微组织及热流模型分析

理想的功率分布是在热处理区能够给出均匀的温度。这需要一个凹形的功率分布，因为加热效应依赖于边缘冷却和表面加热，也就是P/D而不是P/D²，其中P为入射吸收功率。模拟该过程激光束的传播方法如图6.7。它们包括：

①散焦高能多模激光束（凹顶形）。

②单轴或双轴扫描激光束（高强振动的锯齿形）。

③四面体棱镜。

④分段反射镜。

⑤特殊镜片（展像透镜，复曲面反射镜和衍射光学元件）。

这些光束的大多数都用于激光热处理。它们在光束路径的中心区域都产生比较好的均匀功率分布。激光瞬时照射期间，沿深度方向的温度分布能用简单但又理想化的一维热传导模型推导出的方程式来表示。如果该表达式能用的话，一个简单的测试方法就能检测如图6.8的热处理模型的横截面。如果硬化区的底部是扁平的，且平行于横截面中心区以下的表面，那么，一维分析式将会以适当的精确度推算加热材料中的温度（正如第5章中所讨论的一样）。问题是横截面边缘区域是两维的，一维热流模型不能精确地推算诱导温度。究竟是边缘还是中心模型占优势，取决于Peclet数（DvρC/k）^[7]中的处理速度和光束直径。无表面熔化的相变硬化是最简单的算术模型处理^[1]。因为没有熔池，且表面热损失遵循正常的对流和辐射规律，因此它没有未知的对流或潜热期存在^[8，9]。Steen和Courtney^[4]得到了P/（Dv）1/2和硬化深度之间的经验关系，在5.9节有详细描述。正如Sharp和Steen^[7]用有限差分模型所计算的一样，该参数的理论关系见图6.9。Peclet数（DvρC/k）对传播作用的影响是微不足道的。对En8钢，Courtney关系式为：

尽管一维分布对近似预测很有用，但是如果需要更精确的热量分布，必须要进行数值计算，如有限差分模型^[10]。这就要考虑光束能量分布变化、边缘效应、有限局部尺寸和特殊几何形状的影响。同样，如果期望得到硬化宽度的结果，它也是适用的。(www.xing528.com)

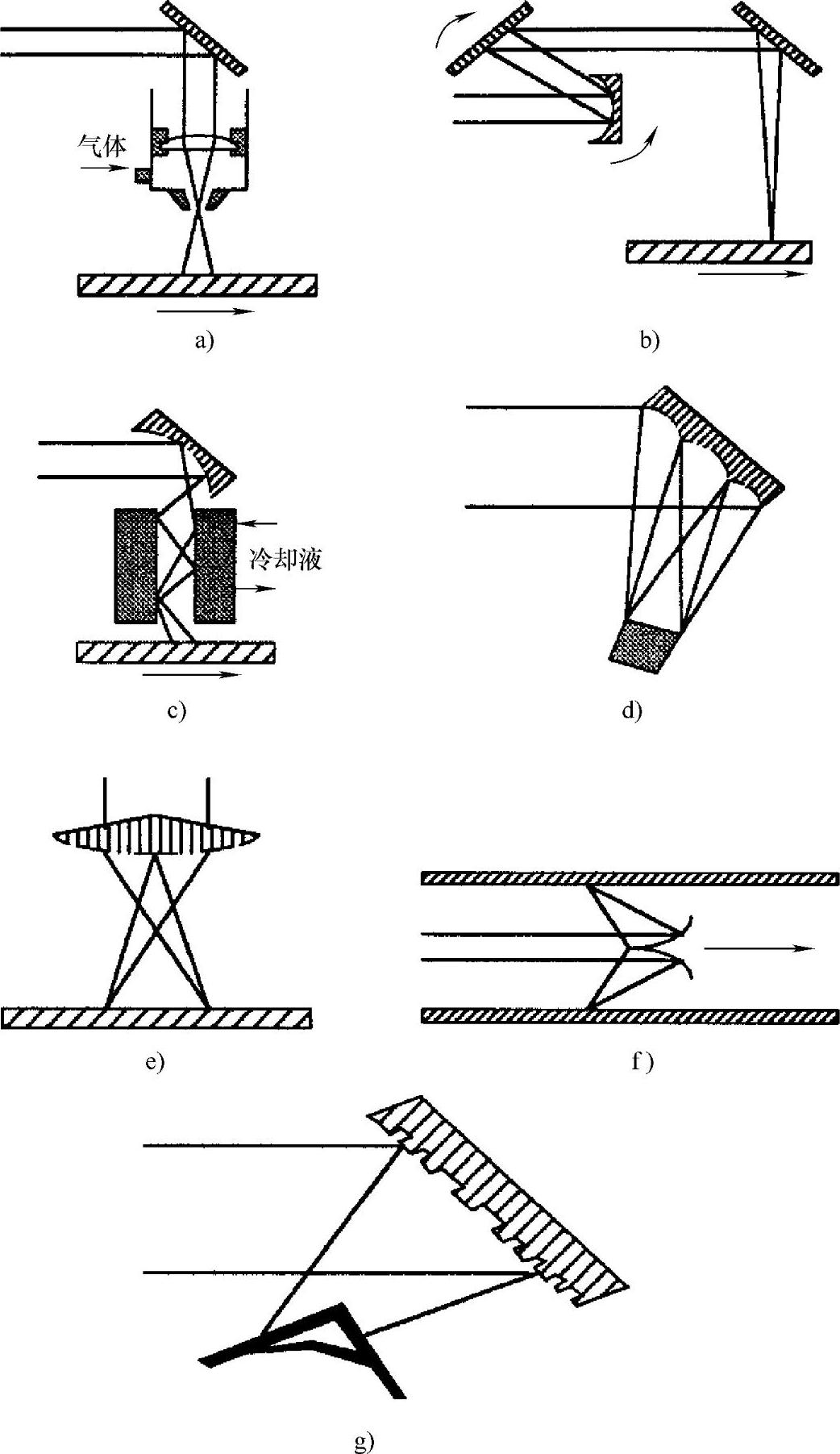
图6.7 激光束的传播方法

a）未聚焦光束 b）修补光束 c）四面体镜 d）光束积分仪（光束分割镜） e）能量分配镜 f）环型镜 g）衍射光学元件

Ashby和Shercliffe^[11]推荐了一种改动很大的模型，用于模拟光束直径。他们曾经解决了放在表面以上特定距离的移动有限线能源的问题。他们提出的总图见前面图5.7。从该图可以看出，与相变硬化的结果非常吻合。

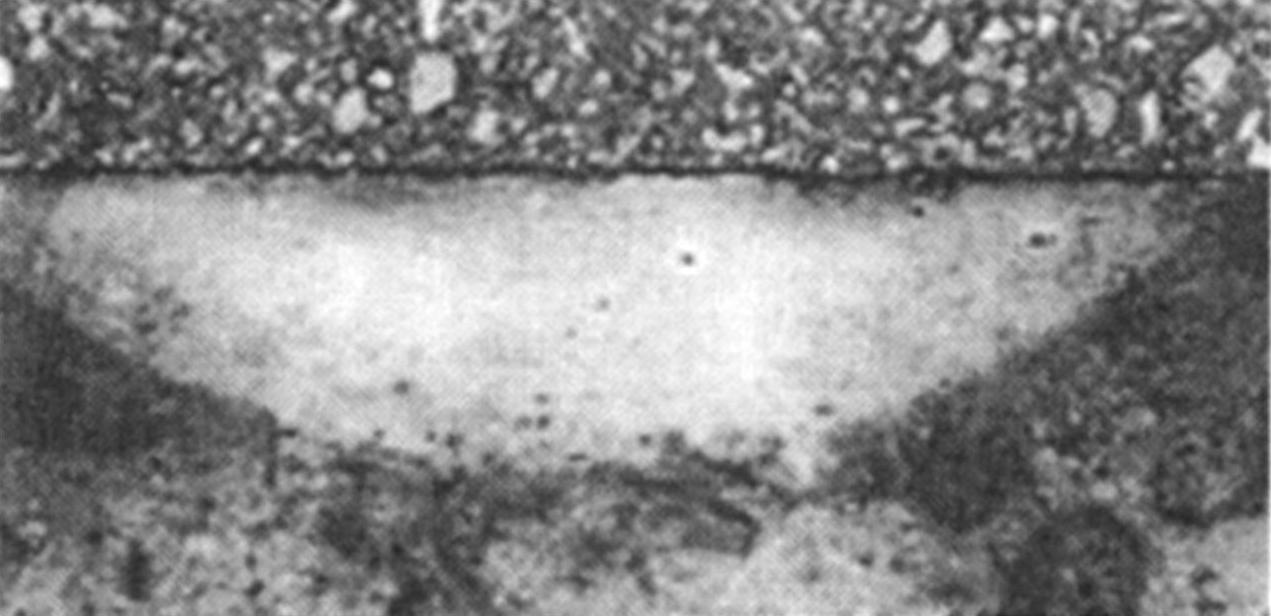
图6.8 En24钢激光相变硬化的显微组织

功率1.6kW，移动速度15mm/s，光束直径6mm。成分（wt%）：C 0.36～0.44；Si0.1～0.35；Mn 0.45～0.7；P最大为0.035；S最大为0.04；Cr 1.0～1.4；Mo 0.2～0.35；Ni 1.3～1.7