有许多半定量模型,比如5.2节中计算HAZ,这里我们主要介绍的是Klemens[22]模型。假设只有径向热流动,并建立了如下匙孔热平衡方程
P(r)=-k(∂T/∂r)2πr (5.22)
如果激光功率只是被具有半径为rc匙孔的等离子体吸收,从“顶帽”模式(均匀阶梯函数)可得
P(r)=Wπr2c=P (5.23)
这里W是单位面积单位深度的功率(W/m2)/m
对式(5.22)进行积分并采用式(5.23)中的边界条件可以得到:
(P/2πk)[ln(r/rc)]=Tc-T (5.24)
此处Tc是等离子体温度K。
在匙孔边缘r=r0以及T=Tv,气化温度单位为K,可以推出如下公式:
r/rc=exp[2πk(Tc-Tv)/P] (5.25)
由此我们对匙孔内的结构以及温度有了一些概念上的理解。Klemen文章中另一个亮点是:估计出了匙孔的尺寸,并且在上部存在一个颈缩。其他采用半定量模型在Steen以及Courtney[23]的文章中给出,他们提出的一个观点是:硬化转变深度与P/(VD)1/2成正比。理由如下:等温线的穿透深度由热传导定律决定,这涉及傅里叶数。因此这个等温线的深度由(Δx2/αt)给出。某一等温线的温度值由热强度值确定,即P/D。移动盘状热源的加热时间由某些量(如D/V)给出。假设依赖关系均为线性关系,可以得到如下方程:
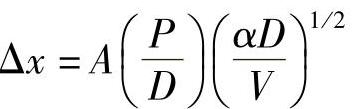
由此可得

该式与实验符合得非常好。
Steen以及Powell[24]进一步研究了激光熔化面下凝固面的移动情况。结果表明,如果操作条件正确,界面区很可能在形成熔合连接后很快凝固。
Olsen[25]计算了切割过程中切割面的熔化深度,他们采用了简洁的推理。切割面上的熔化膜由熔体热传导形成,在切口处形成后被辅助气体吹走。因此可以定义两个厚度,分别由传导以及气压描述。
传导厚度tcond可以由傅里叶第一定律导出。给定切割速度u(m/s)下的熔化热q(W/单位厚度)由下式给出:(https://www.xing528.com)
q=uwρ[(Tm-T0)Cp+Lm]
w是切割的宽度,Tm是液—固界面保持熔点。
从傅里叶第一定律可以看出热量由熔体传导供给。它忽略了对流的影响,并认为切割深度范围内的温度变化不显著。这一点可以得到保证,因为熔体表面温度一直保持在沸点以上。因此可以假设膜层很薄,温度梯度近似于线性。
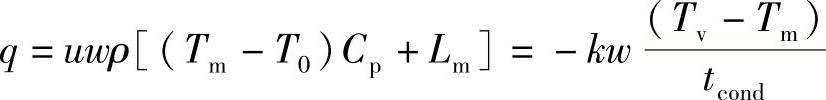
其中 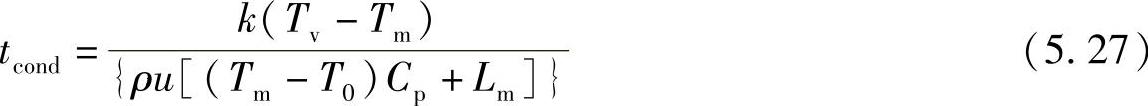
动量控制的厚度tmom可以从切口处深度范围内驱动薄膜的压力降低ΔP,以及气相牵引力计算出来。假设牵引力与总的压强降相比可以忽略,那么以一定速率运动的熔体处于产生以及排除的平衡状态,可用下面的方程描述:
[tmomv]=hu
这里h是切口的厚度,单位为m。
熔体的运动速度近似地由能量平衡方程给出:
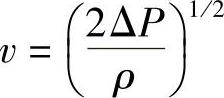
因此 
这两个厚度应该相同,因此不同工艺条件下膜层厚度,比如不同辅助气体压力,可以从图5.15估计出。
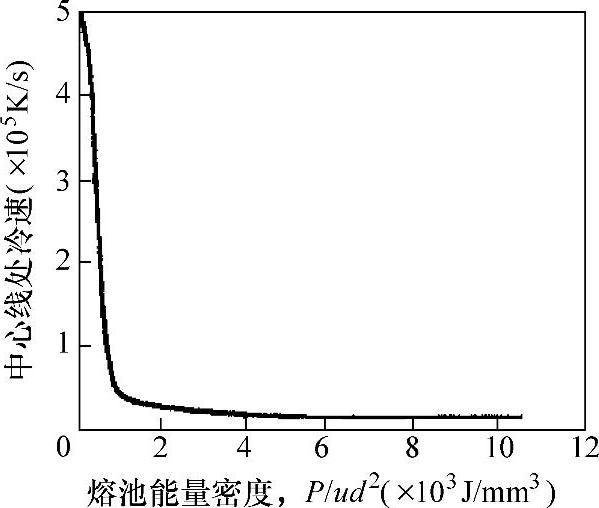
图5.14 中心线冷却速率与熔池能量密度关系的有限差分解
冷却速率将决定凝固过程的结构(见第6章以及文献[21])。
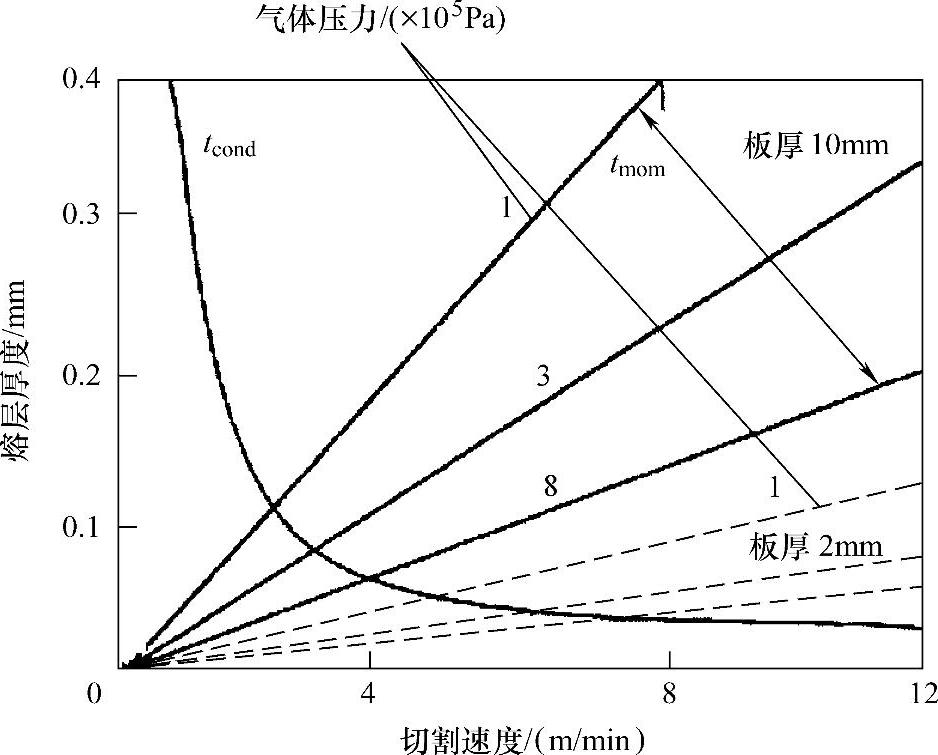
图5.15 不同厚度板材以及不同辅助气体压力切割熔化面厚度的理论估计值
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




