优化有限差分模型的空间划分方法及边界条件研究

有限差分或者有限元模型都是从傅立叶第二定律求解得到的，不同的边界条件有不同的特解。有限差分模型把所研究的空间划分为许多小网格，如Mazumder以及Steen^[16]首先采用指数型网格进行少量计算，来估计热量传播范围以及所需要考虑的体积。由于采用正则矩阵计算更稳定，一旦尺寸确定，就可以转换到正则矩阵计算。对任一小网格，需要保持热平衡。例如，图5.11中的小微元，其加热或者冷却都可以采用傅立叶第二定律描述

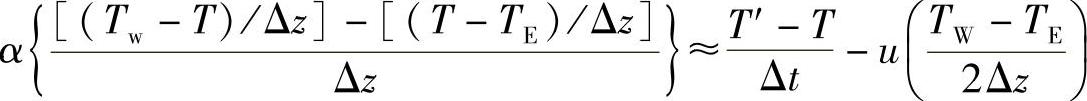
因此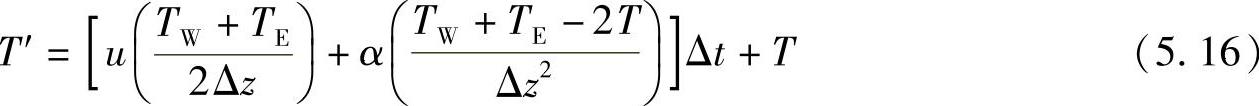

已知本时刻的温度，为了得到时间间隔Δt后的温度，需要求解包括所有点的三维差分方程，需要计算整个矩阵。由于两个梯度项作用于时间t=t，而温度变化作用在t=t+Δt/2，会引起计算不稳定。有时应用Crank-Nicholson^[17]方法来克服此问题，但可能同时降低计算效率。

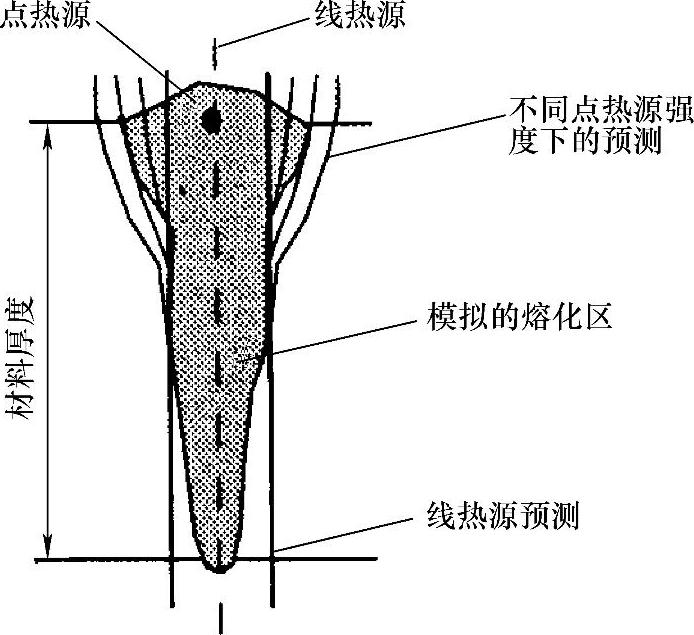
图5.10 点-线热源模型求解示意图

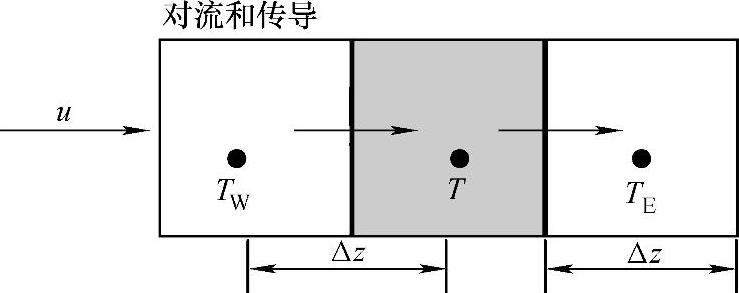
图5.11 方程（5.16）符号示意图

如果是一个准静态问题，比如激光作用下熔池在基板的移动，那么时间项可以去掉，解可以通过所谓的“弛豫”过程来求出。Mazumder以及Steen^[16]曾采用这种方式进行计算，在这种计算方式下热量的加和应该等于零，如果没有等于零，那么稳态的温度场被缓慢地改变，直到热量加和等于零。

如果发生了熔化，可以采用异常比热方式来处理相变潜热。Henry等人^[18]将熔化的比热写成阶梯函数来处理潜热。

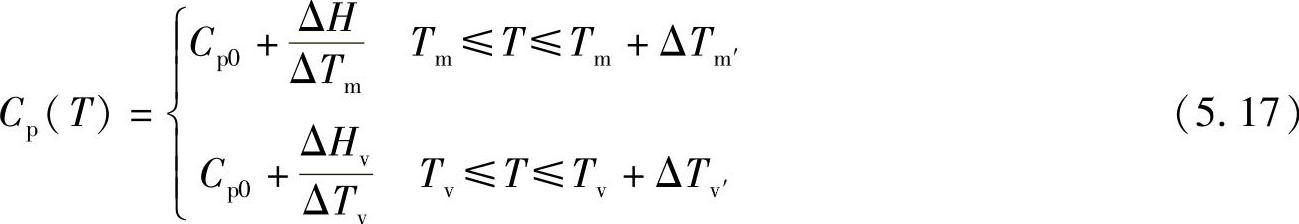
此处C_p0是正常的比热常数，ΔH_v，ΔH_m分别是气化热以及熔化潜热，ΔT_v，ΔT_m分别是气化以及熔化相变发生的温度区间。

边界处点与内部具有相同的热平衡关系，但是温度梯度扩展到外部必须做一定的改变，因为外部温度无法计算。

表面处性质可以从表面温度梯度计算：

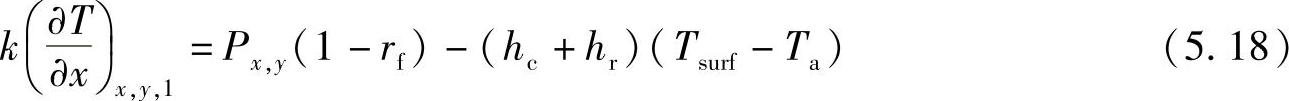(www.xing528.com)

这里T_a是环境温度，P_x，y的值依赖于激光功率分布，比如对于高斯型的激光输出模式，TEM00，P_x，y被定义为：

这里r²=x²+y²

表面沸腾也可以在计算中计入。假设基底某处温度达到沸点，该点金属蒸发后消失，激光直接作用于下面的基底，激光与气化后的金属作用发生等离子体吸收损失一部分光强。光吸收可以用比尔·朗伯吸收定律进行描述^[19]

此处β是吸收系数，单位是m^-1。

所研究平板侧面上的点可以认为离光源较远，∂T/∂x以及∂T/∂y≈0；厚基板底面上的点可以认为∂T/∂z≈0；但是薄基板底面点的温度梯度则需要从整个基板的温度梯度估计出，如下式：

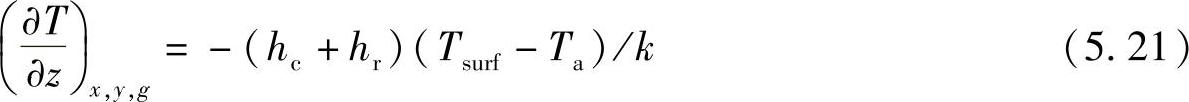
本节只是向不熟悉这些技术的读者展示该模型的通用性，几乎任何物理现象都可以容易地添加，显然它已成为研究机制过程中强有力的工具。然而由于模型平均只需要0.5M字节内存，在计算机上只需要计算几分钟，它还无法用来预测结果以及控制工艺参数。图5.12～图5.14以及图4.31是利用此方法计算的实例。

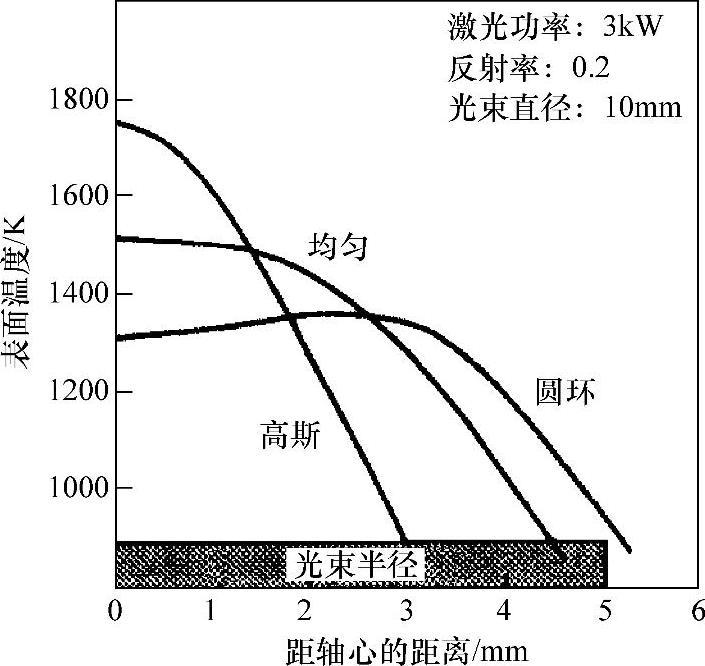
图5.12 模式结构对表面温度分布的影响：有限差分解^[20]

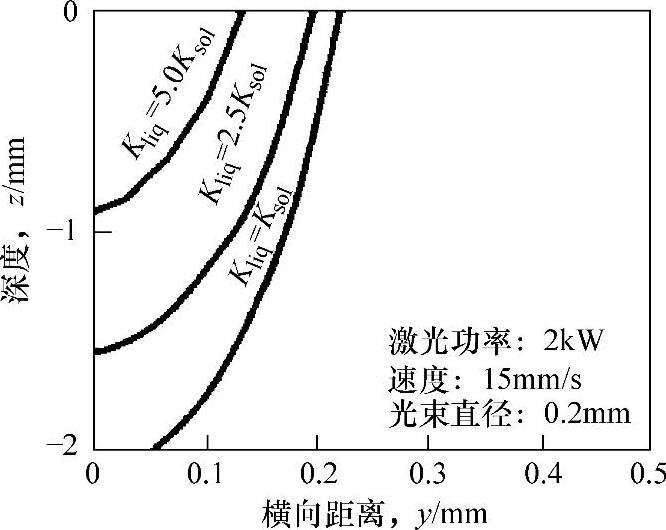
图5.13 有限差分解说明熔池热导率对熔池尺寸的影响

有效热导率由材料热导率、对流以及逆流构成。这个计算说明了搅拌作用对熔池形状以及尺寸的影响^[21]。