材料激光工艺匙孔模型的线热源解

移动线源Rosenthal^[5]的解假设能量是沿深度方向非均匀吸收，其他Rosenthal模型也基于这种假设。图5.8说明了这种热流模式，这种解能够模拟薄层材料单次扫描焊接以及完全穿过锁孔，解如下^[5]：

边界条件是

，，

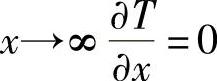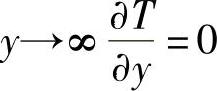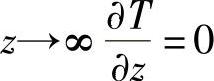
以及

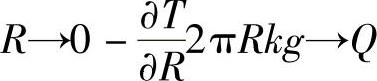
此处

R——到热源的距离（米）=（x²+y²）^1/2（m）；

T——点（x，y）的温度（K）；

T₀——平板初始温度（K）；

Q——单位时间的热量输入=P（1-r_f）（W）；

v——焊接速度（m/s）；

g——板材厚度（m）；

k——热导率[W/（m·K）]；

α——热扩散系数（m²/s）；

K₀——第二类零阶Bessel函数。

（在处理柱状对称的热量扩散以及其他问题时，Bessel函数有时被叫做柱函数，此时第一类Bessel函数被称为“Bessel函数”，

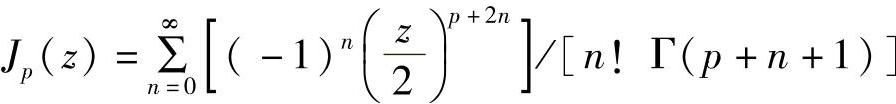
这里Γ（p+n+1）=（p+n）！

第二类Bessel函数被称为Neumann函数

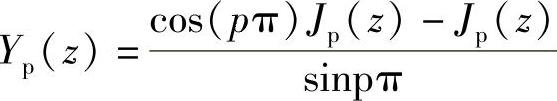(www.xing528.com)

这些函数有函数表，但难于求解。

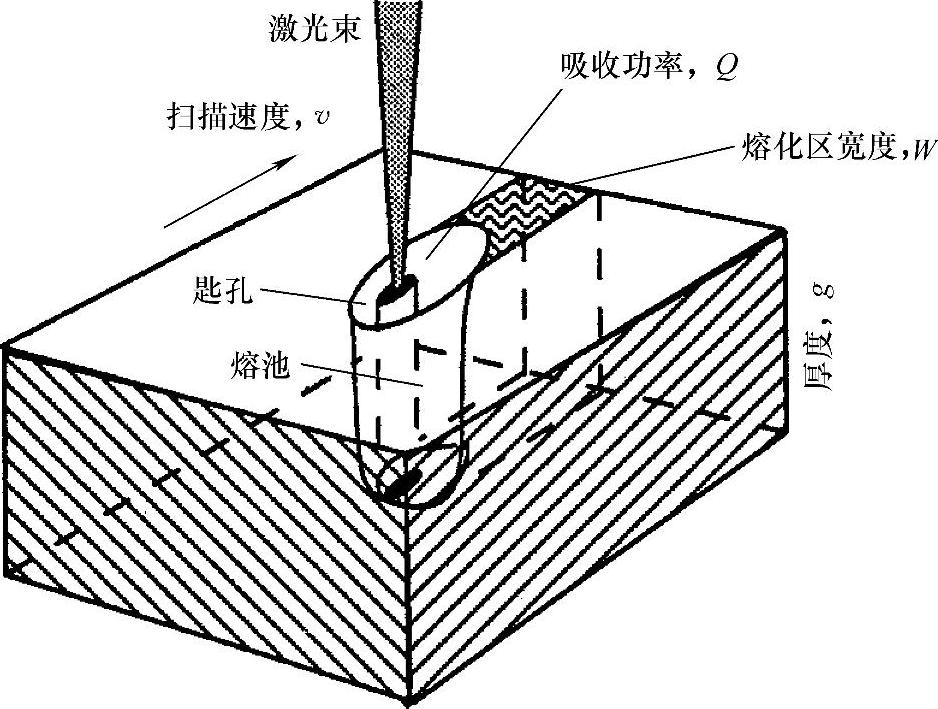
图5.8 匙孔周围熔体的近似几何形状

从方程（5.14）得出中心线x＞0，y=0，Peclet数vx/2a＞＞1，（高速情况下）渐进解为^[11]：

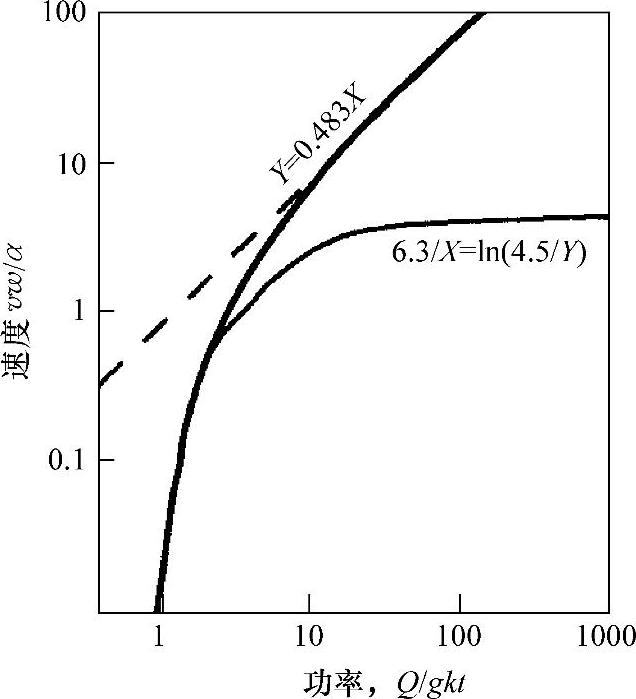
图5.9 归一化速度与归一化功率之间的关系曲线，移动线源解^[12]

可以看出，到目前为止我们得出的关系式都是关于两个无量纲组[vR/2α]和{Q/[2π（T-T₀）kg]}。Swifthook和Gick^[12]发现在高速以及低速情况下存在Bessel函数的解析解，在图5.9中绘出了部分情况。高速极限在第4章4.4.1节中进行了讨论，低速极限下不容易直观地理解。图5.9在预测焊接所需功率以及光束速度方面非常有用。例如采用激光束以10mm/s的速度焊接10mm厚的304不锈钢。按照通常激光焊接宽度1.5mm，假设有90%的能量被匙孔吸收，那么需要多大的激光功率才能进行焊接呢？

304不锈钢的热学性质为：

热扩散系数，α=0.49×10^-5（m²/s）

热导率，k=100（W/m·K）

熔点，T_m=1527℃

解得：

Y=vw/α=（0.01×0.0015）/0.49×10^-5=3.06

从图5.9，或者从方程Y=0.483X，

X=7.0=Q/gkT=Q/0.01×100×1527

可得

Q=10.6kW

考虑到能量吸收率为90%，那么需要的激光功率为10.6/0.9=11.8kW。

这个功率很大，能够高速焊接厚不锈钢板，如果我们只有2kW的激光功率，那么我们可以重新计算焊接速度，这个问题留给读者自己求解。可以看出这些计算是假设能够穿透匙孔并且光束可以聚焦得很细。所有计算都面临同样的问题：实验光束直径附近的温度计算结果很差。这些限制可以某种程度上利用Bunting和Cornfield所采用的柱状热源解^[13]，或者采用有限元或有限差分方法加以克服。