一维热流分析模型探析

如果热传导只在一个方向，并且没有对流以及热源，那么基本方程可以简化为下式：

如果进一步简化，假设无限大表面上热量输入不随时间变化，材料热性质也是均匀的，没有辐射损失以及熔化，那么边界条件可以写成如下形式：当z=0时

表面功率密度，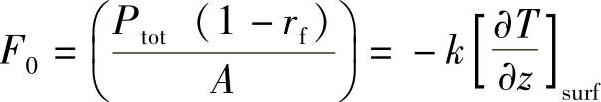

当z=∞时

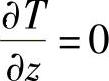
当t=0时，T=T₀

该方程的解是：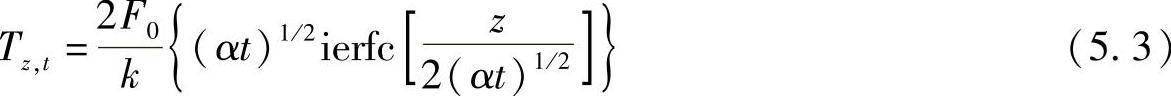

此处ierfc是积分误差函数，其数学表达式为：

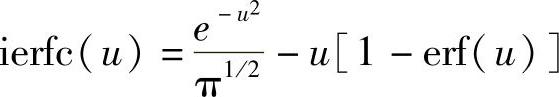
由于误差函数包含对数项，对它进行代数运算非常困难，可以采用多项式替换，每一项精度高于2.5×10^-5，足以满足我们的需要。下面是多项式形式^[2]：

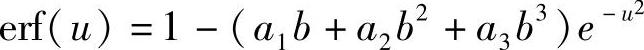
此处

b=（1+cu）-1；

a₁=0.3480242；

a₂=-0.0958798；

a₃=0.7478556；

c=0.47047。

（巧合的是误差函数也被定义为：

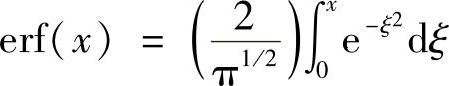
对其进行微分

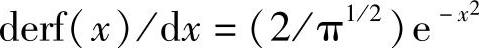
在极限处误差函数值为： erf（0）=0，erf（∞）=1）(www.xing528.com)

如果激光关闭，材料随之冷却，材料的温度变化可由下式给出：

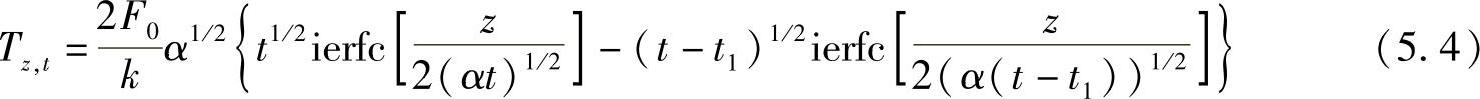
此处 T——温度（℃）；

z——深度（m）；

t——时间（s）；

t₁——关闭激光时间（s）；

k——热导率[W/（m·K）]；

α——热扩散系数（m²/s）；

F₀——吸收的功率密度（W/m²）。

该模型使人们对有关一维热传导范围有了感性认识，当热源远远大于传导深度，或者热流沿柱状工件传输，一维模型无疑是恰当的。然而该模型不能进一步改变，光束尺寸、模式结构等参数无法引入，加热速度只能通过加热时间来模拟，工件厚度也无法引入。表5.1给出了Brienan和Kear所做出的一些典型解^[3]。

表5.1 镍片的加热以及冷却（深度0.025mm）时间随功率变化^[3]

这个模型得出的解很有用，Brienan和Kear^[3]绘制出了一维加热方式下，该模型预测的冷却速率、热梯度以及凝固速率，图5.2～图5.5给出了纯镍的结果。

巧合的是，方程（5.3）显示出热传导主要集中在[z/2（αt）1/2]=1范围内，傅里叶数=1。当z=0时，2ierfc（1）=0.1005以及2ierfc（0）=1.1284。在任意时刻，90%的温度变化在此深度范围内。这可以让我们对传导损失的热量进行简单而有意义的估计，比如[z_F=1ρC_p（T_surf/2）]是传导热损失。

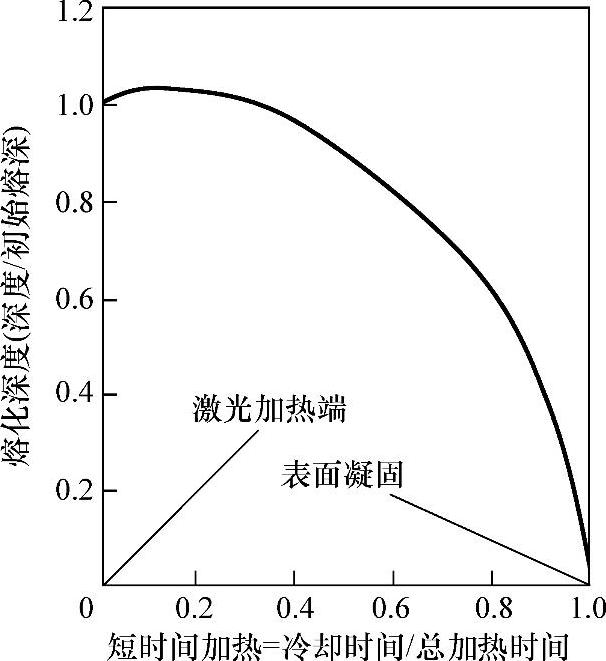
图5.2 纯镍在Q=500000W/cm²吸收功率密度下熔化深度变化过程

初始熔化深度为1.2mm，最高温度为2038℃^[3]。

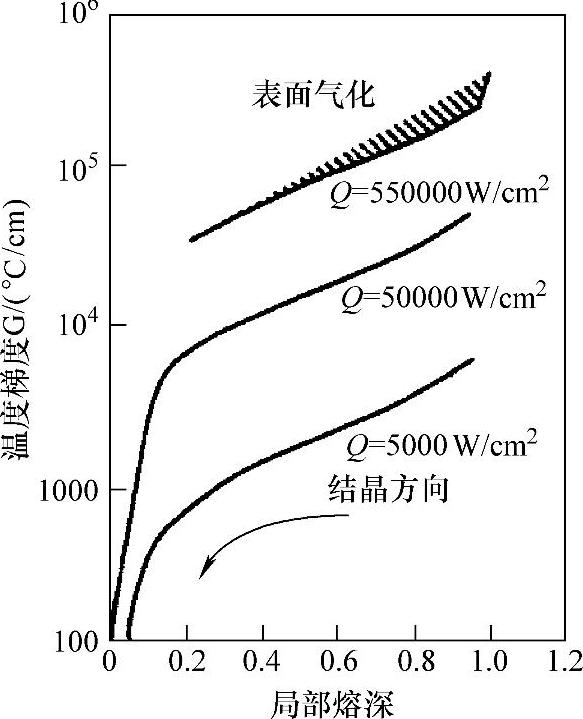
图5.3 纯镍熔化面温度梯度的瞬态行为，初始熔化深度为0.025mm

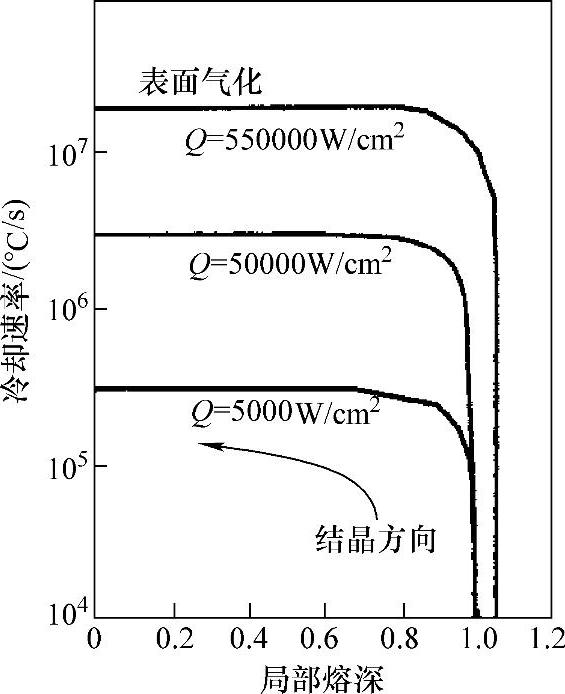
图5.4 纯镍冷却速率的瞬态行为（条件与图5.3相同）