模式与光束直径在2.7.3中的优化

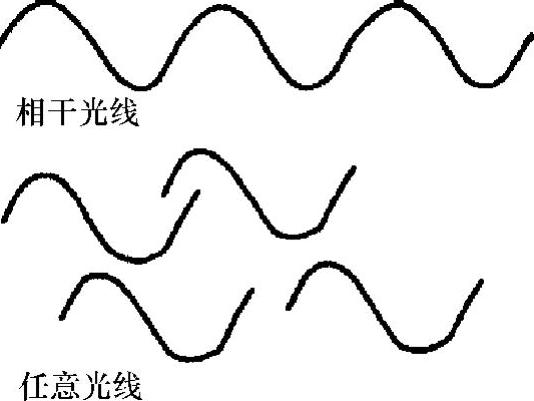
图2.11 相干光线和任意光线的电矢量相位比较

激光器的谐振腔就是一个光学振动器，当谐振腔产生振动的时候，将在振动小室内产生标准的电磁波，当然形成的电磁波还要取决于小室的形状，可以根据小室的情况计算出可能产生的波的模式，在角度轻微变化的条件下，可以产生大量的轴向标准波，偏离轴向标准波的数量与Fresnel数（a²/λL）有关（见1.1.1.3节），这些标准波与在小室内的横向标准波产生干涉，对非放大圆柱腔，横向标准波的振幅E（r，ϕ）以Laguerre-Gaussian函数分布的形式给出：

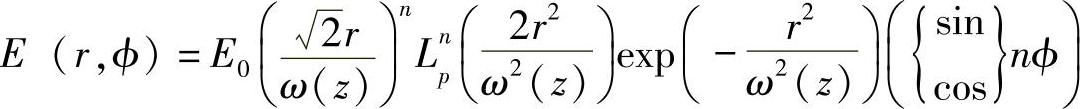
式中 E（r，ϕ）——在r、ϕ位置的振幅；

ω（z）——在z点的光束半径；

r——光斑半径；

n——整数；

ϕ——角度位置。

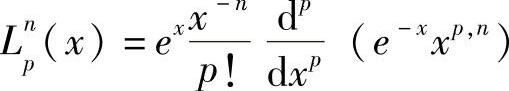，该式为通用的Laguerre多项式。

一些低阶的多项式如下：

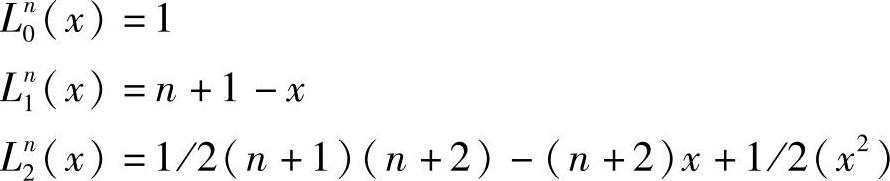
强度分布可由振幅的平方得到：

P（r，ϕ）=E²（r，ϕ）这就是圆形光束的经典分布模式，方形光束的分布模式与Hermite多项式相似，代表了各种模数的振幅和空间强度分布的曲线见图2.12和图2.13，图2.14是产生各种光束的典型模式。

这些横向电磁波模式（TEM_plq）的分类如下：(www.xing528.com)

p——零场半径数；

l——零场角度数；

q——零场轴向数。

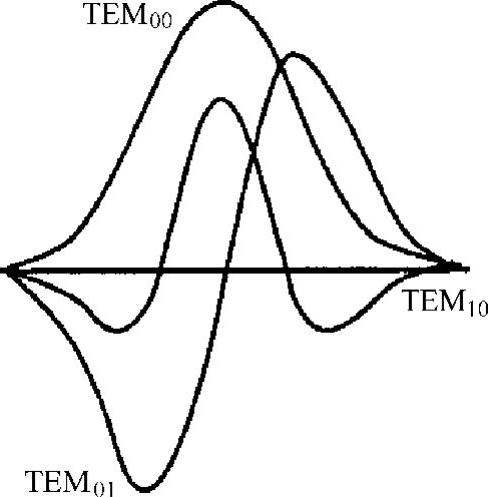
图2.12 各种激光模式的振幅变化

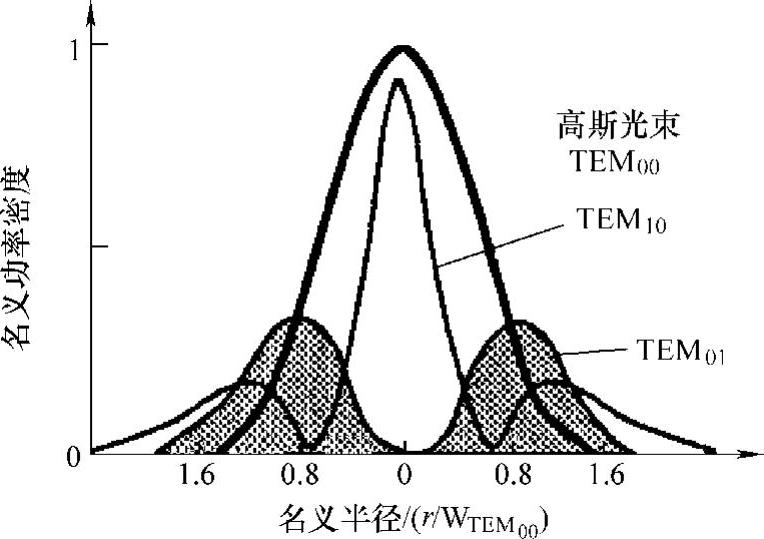
图2.13 各种激光模式的强度分布

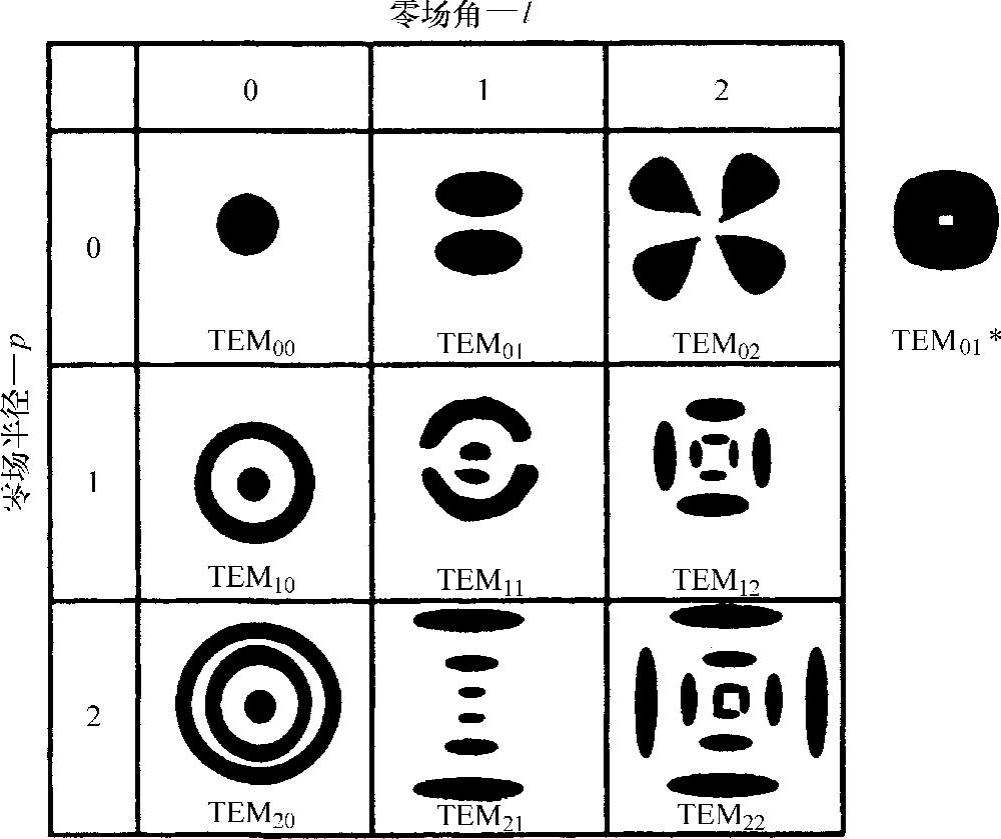
图2.14 各种激光模式的图案

多数SF激光器是以近似完美的TEM₀₀或TEM₀₁^∗模式运行，TEM₀₁^∗模式是从图2.14中两个互相垂直的TEM₀₁模式的振动中产生的。

由于FAF激光器具有长而窄的振荡管（较低的Fresnel数，a²/λL），其发出的光束具有低阶模特征（见1.1.1.3节），由于等离子密度的变化，从这种激光器发出的激光模式将发生轻微的变形。

TF激光器通常产生不确定的高阶多模激光束，当为单一谐振腔时其得到的是高斯光束，或者由于谐振腔内热气体的横向运动导致腔体横向长大得到非对称光束，为减少上述现象的影响，一些腔体设计成如1.2.1.3节所描述的环形。

由于光束不是来自于有效的点，光束模式越高，因此将平行光束聚焦为细小的斑点就更加困难。

在材料加工过程中会出现一个光束斑点问题，例如图2.12和图2.13计算得到的理论半径ω（z）都相同，该理论值与影响加热效果的实际半径没有关系。Sharp^[20]认为光束直径应当定义为总功率的1/e²范围内（见第10章中关于光斑直径的测量方法）。