基于灵敏度分析的二维预锻成形工艺优化方法

在锻造工艺中，很多零件由于形状复杂，无法直接一次成形，或者一次成形容易产生严重的质量问题。为此，需要根据工艺要求，设计合理的预锻工步。关于预锻工艺设计，有很多种方法，如基于经验的方法和正交试验方法等。这里介绍一种基于有限元和灵敏度分析的预锻设计优化方法。

弹塑性材料大变形过程的灵敏度分析法由Badri-narayanan和Zabaras提出，Fourment等人也提出一种用于预锻模形状设计优化的方法，目标函数为理想锻件形状与实际锻件形状的距离。预成形和预锻模具形状用B样条曲线拟合，设计变量为B样条曲线控制点的法向距离。赵国群等人则以终锻件形状与理想锻件形状不重合区域的面积作为目标函数。采用三次B样条函数表示二维成形问题的预锻模具形状，B样条曲线的控制点作为设计变量。设目标函数为：

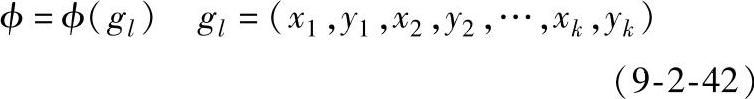
其中k为B样条函数控制点的数目。对这种无约束的优化设计问题，可采用BFGS优化方法进行优化。根据上述给出的目标函数表达式，目标函数对优化设计变量梯度如下：

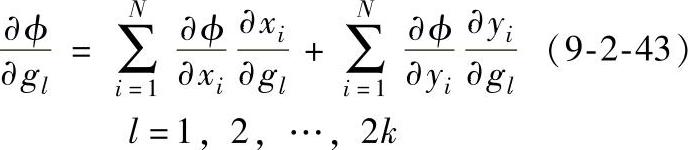
上式中∂ϕ/∂x_i和∂ϕ/∂y_i可以通过目标函数获得，∂x_i/∂g_l和∂y_i/∂g_l的可以通过下面的表达式获得。利用速度矢量V刷新节点的坐标：

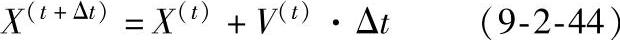
可得节点坐标关于设计变量的偏微分表达式为：

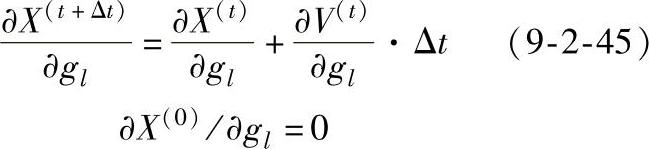
因此，节点速度关于设计变量的灵敏度已知时，即可求得目标函数关于设计变量的梯度。根据有限元理论，金属成形问题的单元刚度方程可以表示为：

K（X，V）V+F（X，V）=0 （9-2-46）

上式关于g_l求偏导数可得：

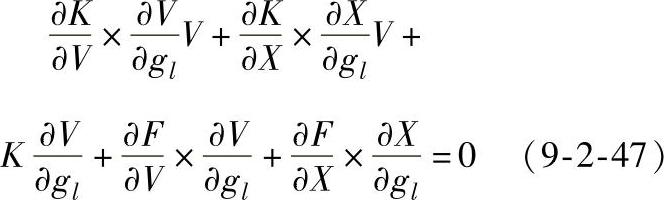
上式可以简化为：

RV_，gl=F_，gl

式中 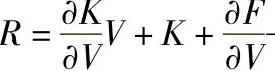——单元的刚度矩阵灵敏度；(www.xing528.com)

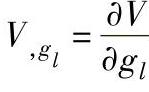——节点速度相对于第l个设计变量的灵敏度列阵；

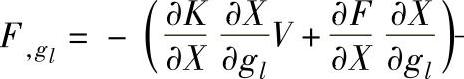——单元的节点力的灵敏度列阵。

以二维问题为例，采用四节点四边形等参单元时有：

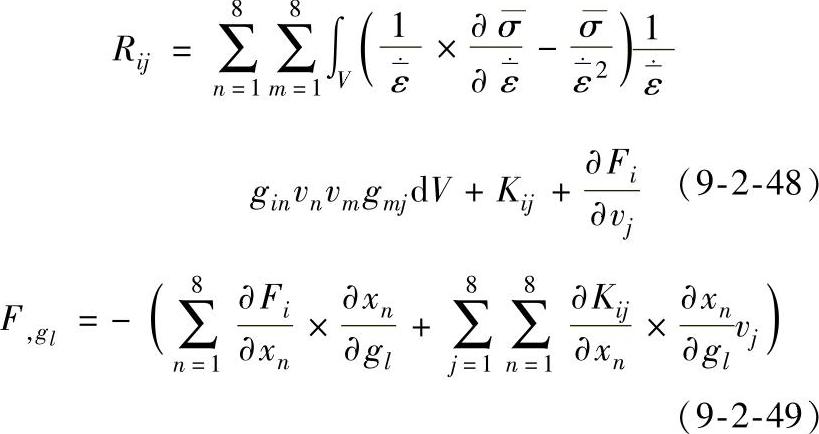
（i，j=1，2，…，8）

通过单元刚度矩阵集成，建立如下线性代数方程组：

对于预成形过程的给定初始解，完成预成形过程的数值模拟后，节点速度关于设计变量的灵敏度可通过上式计算得到。终锻过程模拟时，边界节点速度关于设计变量的灵敏度为0，因为终锻模的形状保持不变。终锻模拟结束后，根据式（9-2-42），节点坐标关于设计变量的灵敏度将用于计算目标函数和梯度。上述计算过程结束后，以BFGS为核心的优化程序将判断优化条件是否满足，如果没有满足，则产生新的预锻模形状的控制点坐标。

如图9-2-13所示为一上下几何尺寸不对称的回转体零件，上下模具截面曲线共有22个控制点。假定预锻结束时上模和下模中心位置的间距为40mm，终锻时相应的间距为17.2mm。成形过程简化为等温成形，摩擦因数为m=0.2，流动应力模型为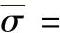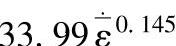。根据上述优化方法进行优化，图9-2-14所示为优化的历史，随着优化迭代，终锻模腔在保证充分填满的情况下，飞边变得越来越小。图9-2-15所示为目标函数在优化过程中的变化情况。

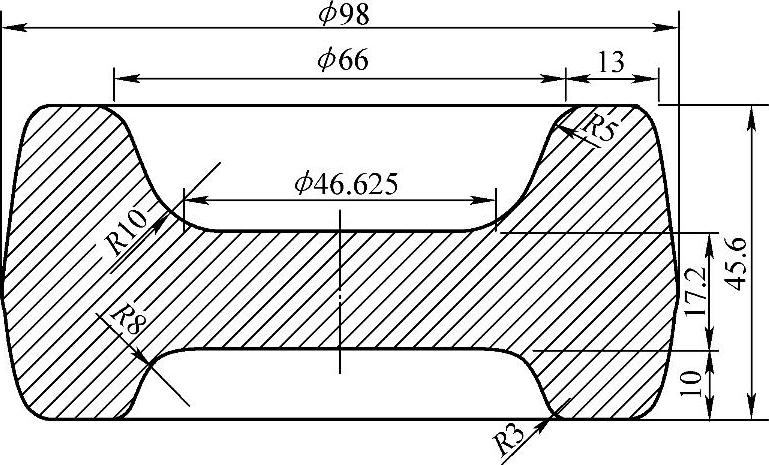
图9-2-13 轴对称锻件形状和尺寸

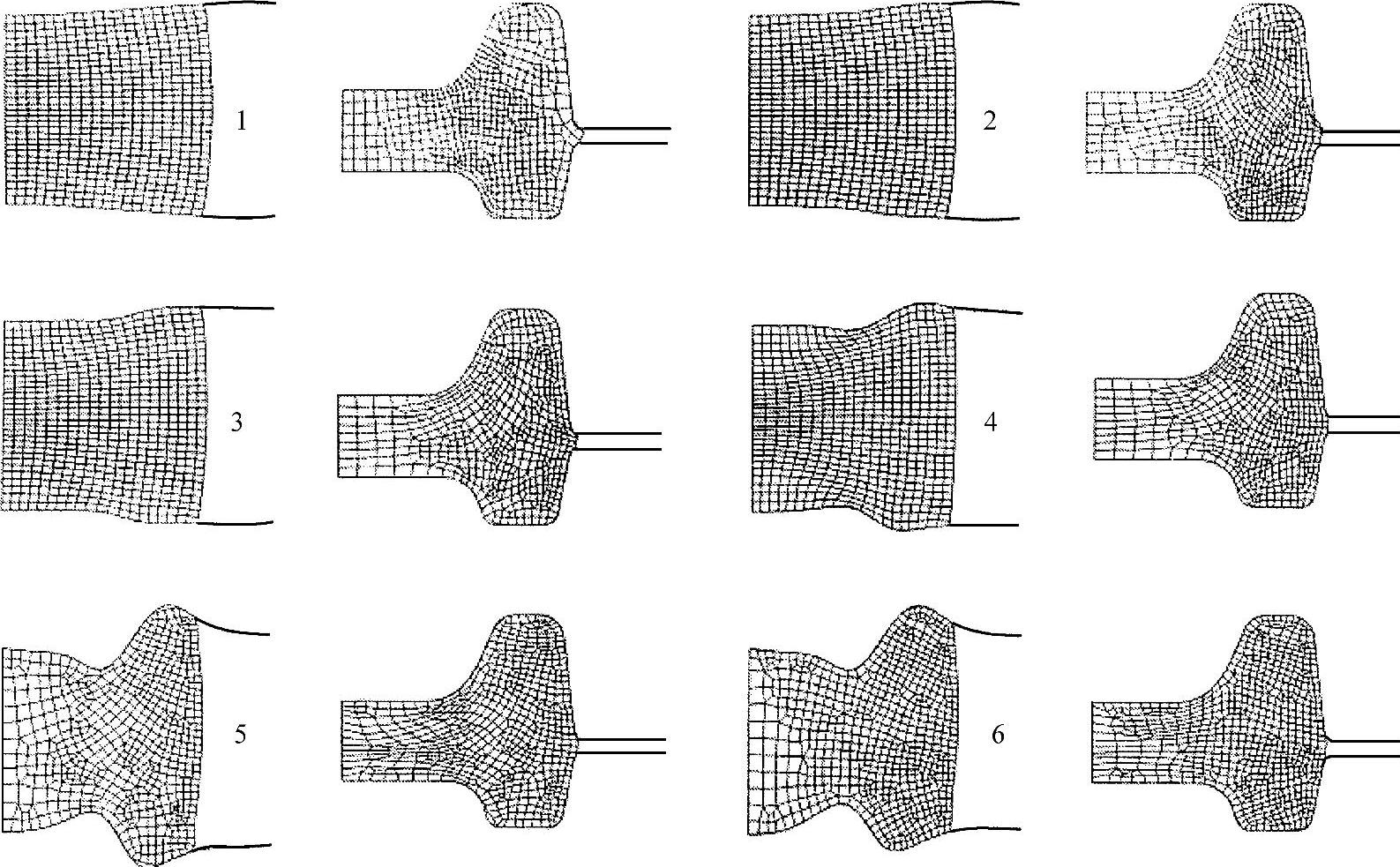
图9-2-14 优化过程预锻模具形状、预锻件形状和终锻件形状的变化情况

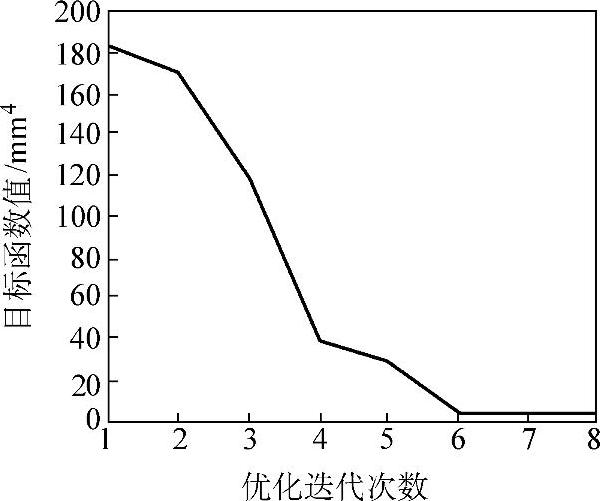
图9-2-15 目标函数在优化过程中的变化情况