齿轮毛坯热锻变形均匀性控制与优化

齿轮是机械传动系统中的关键零件之一，在工作中受力情况比较复杂，作用在齿面上的力通常有脉冲弯曲力、接触应力和摩擦力，齿面的运动同时有滚动和滑动。齿轮的损坏形式主要是疲劳损坏。因此，齿轮寿命的关键是疲劳强度。

传统的齿轮制造工艺为：锻造齿轮毛坯→正火→高温回火→机械加工→碳、氮共渗（并直接淬火）→低温回火。碳氮共渗之前只有一道正火工序（在相变温度以上进行）。所以，锻造遗留下来的粗大晶粒或过热组织就显得十分突出，将影响碳氮共渗的质量和齿轮的内部组织性能。锻件变形越均匀，局部变形差越小，组织就越均匀；相应地，内部组织应力越小，由组织变形不均匀而产生的开裂机会就越小，锻件的疲劳寿命也相对增加。因此，锻造工艺优化使得材料的变形均匀具有重要的意义。

以某型号拖拉机中间轴传动齿轮毛坯锻件作为优化设计实例，齿轮毛坯锻件的热锻件图如图9-2-7所示。采用有限元数值模拟软件DEFORM2D分析齿轮毛坯的等温热锻过程，毛坯为圆形棒料，经过模具镦粗台镦粗后直接放入终锻型槽一次终锻成形。因为零件属于二维轴对称问题，有限元数值模拟计算时，取零件的二维旋转截面进行计算。锻件材料为40Cr，锻造温度为1000℃，模具预热至300℃。毛坯与模具之间的摩擦因数为0.3，上模下行速度近似为50mm/s。

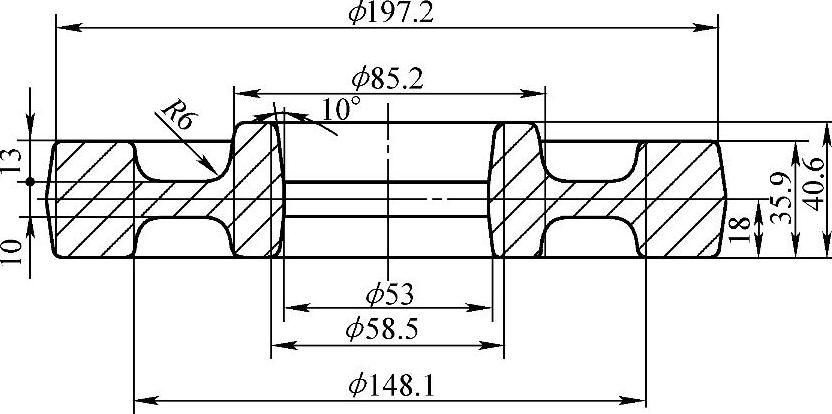
图9-2-7 齿轮毛坯热锻件图

1.目标函数

锻件变形越均匀，由组织变形不均匀而产生的开裂机会就越小，锻件的疲劳寿命也相对增加。以控制锻件变形均匀性为目标，采用除去飞边部分的锻件中所有单元体的等效应变与整个终锻件的平均等效应变的均方差为锻件变形均匀性的指标，即目标函数如式（9-2-36）。

2.设计变量

根据锻模设计经验，经过模具镦粗台镦粗后的毛坯形状（高径比H₀/D₀）、飞边槽桥部尺寸、冲孔连皮厚度和终锻模具型腔圆角半径等参数对锻件的成形性能有重要的影响，因此取上述参数为设计变量，如图9-2-8所示。

3.约束条件

除了应满足材料充满整个模腔的条件，还要考虑设计变量的合理范围。根据锻造工艺设计经验，设计变量的取值范围见表9-2-4。

4.优化过程

如果直接采用12个设计变量进行设计优化，数值模拟和优化迭代时间会很长。因此，首先采用数值模拟程序作为成形过程评价工具，对优化设计变量进行试验设计分析，筛选出重要的因素作为主要的设计变量。然后，采用响应面法对目标函数和设计变量建立近似模型，并利用序列二次规划方法（SQP）进行设计空间寻优迭代。

为了提高DOE分析的效率，在数值试验过程中，通过编制专用程序调用某CAD软件的API函数修改上下模具的几何形状，再修改DEFORM软件的前处理文件（KEY文件），并启动DEFORM软件自动进行数值仿真计算，然后根据模拟结果自动计算目标函数值。L₂₇（3¹³）正交试验的因子和水平见表9-2-5。

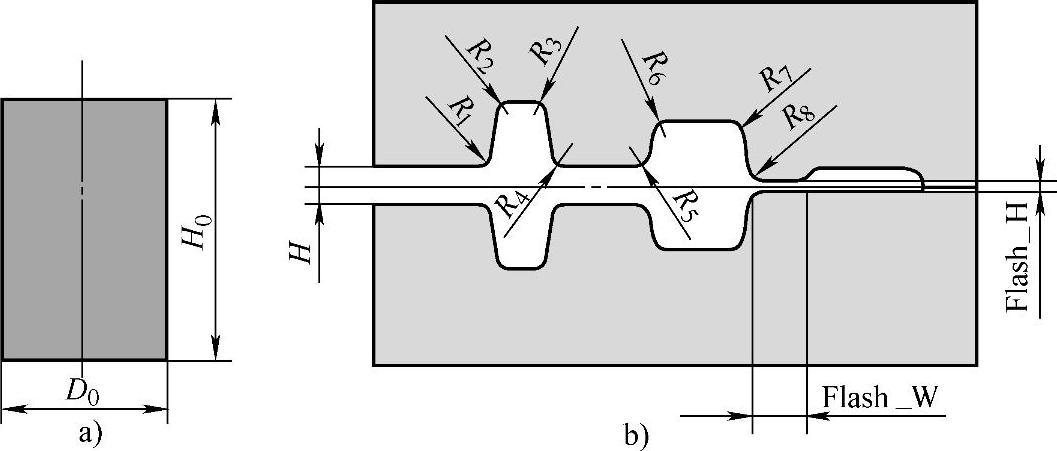
图9-2-8 设计变量

a）坯料形状 b）模具形状

表9-2-4 设计变量的取值范围 （单位：mm）

表9-2-5 DOE试验因子及其试验水平(www.xing528.com)

注：以上设计变量除H₀/D₀外，单位均为mm。

数值模拟结果的方差分析结果见表9-2-6。方差分析发现，H₀/D₀的F值为131.004，远大于F_0.01（2，2），对目标函数高度显著；Flash_H的F值大于F_0.05（2，2），对目标函数影响显著；因素H、R₁的F值大于F_0.1（2，2），对目标函数影响比较显著。其余因素的影响很小，可以忽略。因此，经过方差分析，筛选出因素H₀/D₀、H、Flash_H、R₁作为设计变量，重新构建设计优化模型，齿轮毛坯热锻成形工艺设计优化的规模将大大减小。

针对锻造工艺中无法建立关于目标函数和设计变量的显式函数关系这一问题，如果采用基于梯度的优化算法（如牛顿法、罚函数法）往往由于梯度的求解困难而无法进行。因此可以采用响应面法利用DOE中的部分数据，得到如下二阶响应面模型。该模型的R²为0.98662，说明该模型能足够精确反映目标函数与设计变量之间的关系：

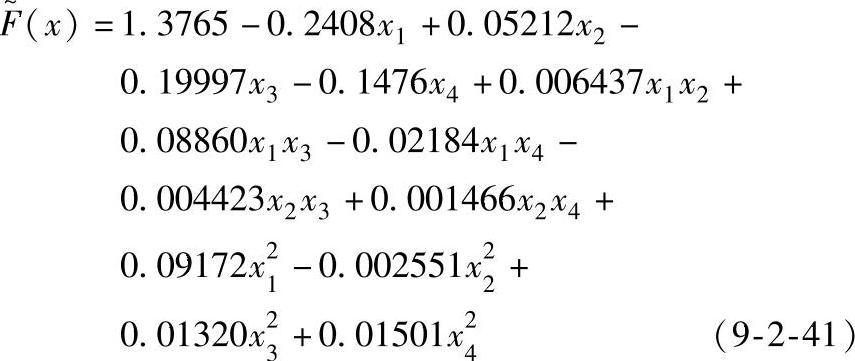
式中 x₁——H₀/D₀；

x₂——H；

x₃——Flash_H；

x₄——R₁。

表9-2-6 方差分析结果

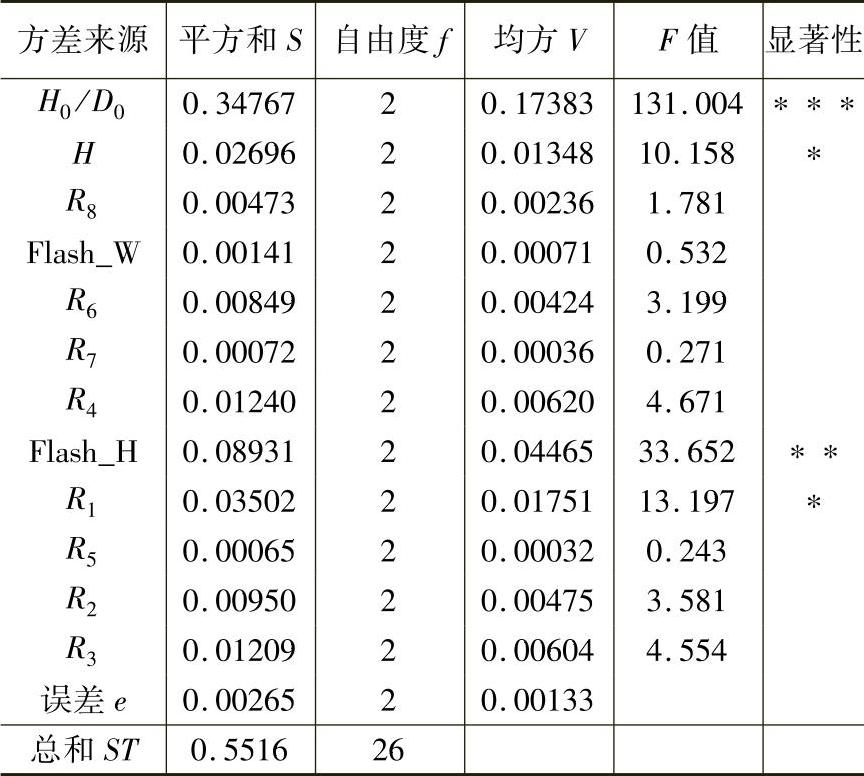
注：F_0.01（2，2）=99.01，F_0.05（2，2）=19，F_0.1（2，2）=9.00高度显著：***，显著：**，比较显著：*。

采用上述模型和SQP算法，对齿轮毛坯热锻成形工艺参数进行优化计算，经过17次迭代运算，得到最优设计参数，如表9-2-7所示。目标函数由最高点0.7914下降到0.4843，下降了38.8%。优化前后锻件的等效应变分布如图9-2-9所示。从图中对比可以看出，等效应变的最大值由4.14降至2.44、等效应变的最小值由0.293降至0.245、等效应变的差值由3.847降至2.195，优化效果明显。

表9-2-7 齿轮热锻成形工艺的最佳设计方案

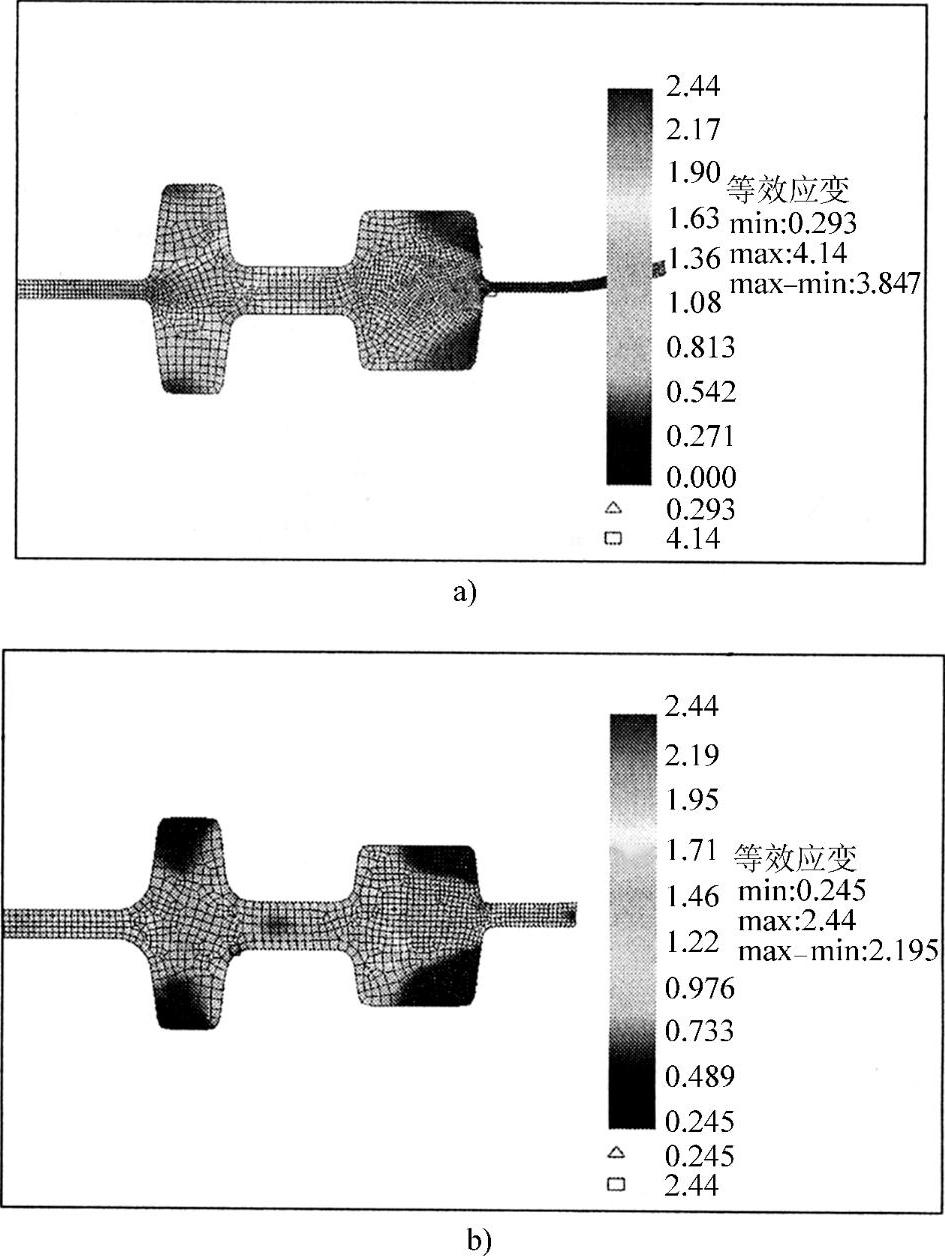
图9-2-9 优化前后的等效应变分布

a）优化前 b）优化后