优化算法的选择与分析

1.优化方法分类使用条件

优化问题的求解方法主要有两类：解析法和数值计算方法。解析法的基本原理是利用数学分析的方法，根据目标函数导数的变化规律与函数极值的关系，求目标函数的极值点。利用解析法寻找极值点的时候，需要计算目标函数的梯度，以便找出稳定的极值点。然后还要对所找到的极值点进行判断，确定是否是最优点。在目标函数比较简单时，求解目标函数的梯度及用海赛矩阵进行判断并不困难。但是，当目标函数比较复杂或为非凸函数时，应用这种方法就会遇到麻烦，有时甚至很难计算目标函数的梯度，更不用说采用海赛矩阵进行判断。此时不宜采用解析法，而可以采用另一种方法，即数值计算方法。

数值计算法通常也称为直接优化方法，是一种数值近似计算方法。基本原理是根据目标函数的变化规律，以适当的步长沿着能使目标函数值下降的方向，逐步逼近到目标函数的最优点或直至达到最优点。这种方法不必求解目标函数的梯度，因而算法容易实现，但其最大的缺点是可能迭代次数太多，导致计算时间长。

本章介绍的优化方法中，序列二次规划属于典型的解析法，而正交试验法、神经网络法、遗传算法和响应面法则属于数值计算方法。对于很多工程问题，数值计算方法可能较为实用。

2.空间搜索策略

对于设计变量与目标函数无法建立明确数学表达式的工程问题，可首先建立设计变量与目标函数之间的近似模型。在优化过程中，用近似模型替代有限元分析程序计算具体的目标函数值，可以减少调用有限元程序的次数，提高优化效率。但是，如果完全采用近似模型代替有限元分析程序进行优化迭代运算，得到的优化结果常存在较大的误差。

具体解决策略是将整个设计空间分解成多个子空间，在子空间内利用近似模型进行优化求解。如果该最优解经目标函数判断，认为改进了设计方案，则需要调用有限元程序计算对目标函数值进行校核。如果近似优化最优解没有得到确认，则改变原有子区域，重新进行近似优化计算。如此往复，直到满足整体迭代条件，获得问题的最优解为止。(www.xing528.com)

关于新优化解的精度的判断，可以采用下式：

式中 f（x^k）、f（x^k+1）——每个子空间优化开始和结

束时目标函数的实际值；

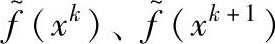——每个子空间优化开始和结束时目标函数的近似模型值。

理论上，如果ρ=1，表明近似模型能很好地描述实际模型；如果ρ＜0，则表明近似模型在当前子区域导致目标函数上升。实际运算中，考虑数值解的误差等问题，如果ρ≤Δρ₀，则可以认为近似模型的计算存在问题；而如果ρ≥1-Δρ₀，说明近似模型精确；如果Δρ₀＜ρ＜1-Δρ₀，说明在当前子空间，尚未达到最优解。Δρ₀的值可根据优化要求确定，取值范围为[0，0.2]。