如何使用响应面法评估预测精度？

响应面法RSM（Response Surface Method）是以试验设计为基础的用于处理多变量问题建模和分析的统计处理技术。最早由G.E.P.Box和K.G.Wilson提出，但初期的响应面法都没有考虑噪声因素，直至1980年R.H.Myers把噪声因素引入响应面法后才在工业界得到广泛的应用。

例如，若某产品的输出特性与温度x₁和压力x₂有关，则可以把观察到的响应量y写成温度和压力的函数，即：

y=f（x₁，x₂）+ε （9-2-17）

如果用E{y}=η表示期望的响应值，则由η=f（x₁，x₂）表示的曲面称为响应面，如图9-2-4所示为响应面在x₁和x₂坐标平面上的等值线投影。

在大部分设计问题中，响应量和设计变量之间的关系形式是未知的。因此，RSM的第一步是求出f（x）的适当近似。最广泛采用的响应面近似函数是使预测响应y～和一组因子x相关的低阶多项式。通常使用二阶多项式（当然，函数形式不局限于多项式）表示响应面如下：

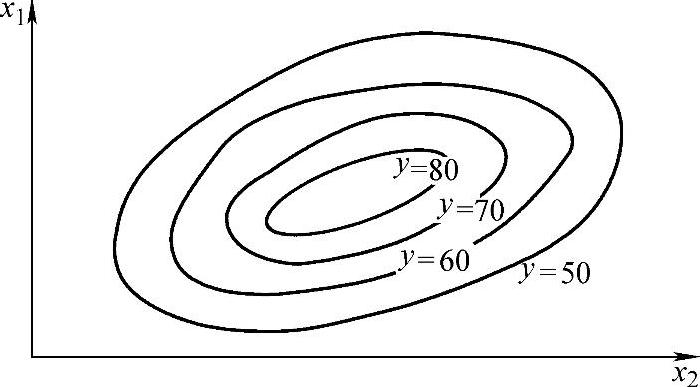
图9-2-4 响应面的等值线

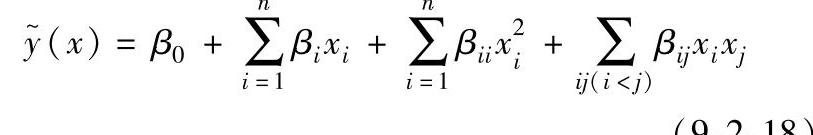
式中 n——自变量总数；

x_i——自变量；

β_i——多项式的待定系数。

对两个变量的情况。响应面表示如下：

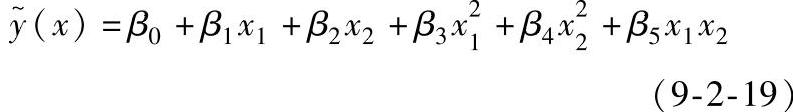
在上式中，令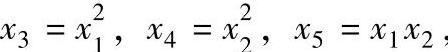则上式可转换成多元线性回归模型，即：

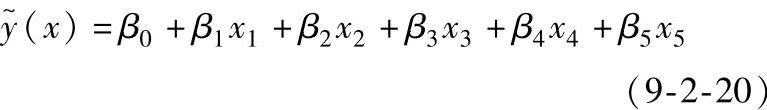
设总的试验次数为n，响应面可用如下矩阵形式表示：

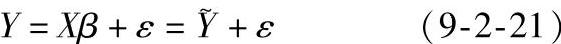
式中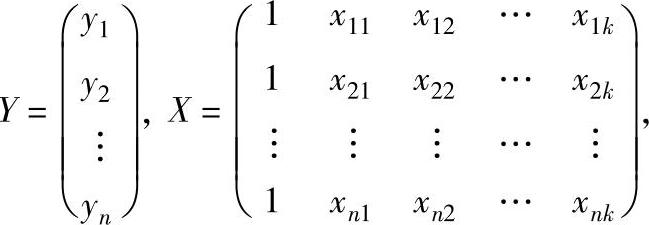

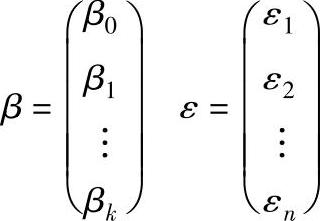
Y为实际观测响应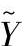，为近似响应，其值由试验数据估计；ε为拟合误差，是一个随机噪声因素。

为了估计参数β₀，β₁，…，β_k，可仍采用最小二乘法，设b₀，b₁，…，b_k分别是参数β₀，β₁，…，β_k^的最小二乘估计。则回归方程为：

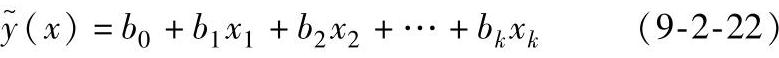
由最小二乘法可知，b₀，b₁，…，b_k应使全部观测值y_i与回归值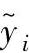之间的偏差平方和Q达到最小，即：

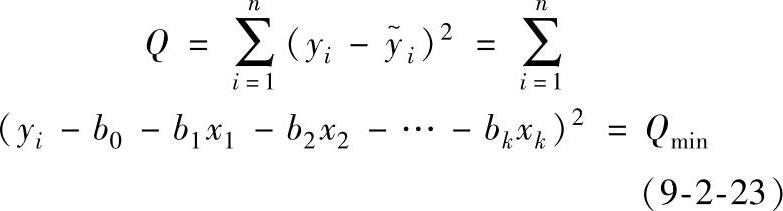
根据极值定理知b₀，b₁，…，b_k应是下列方程组的解：(www.xing528.com)

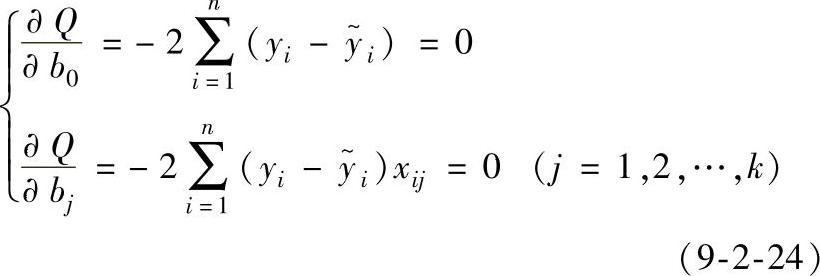
解以上方程组可得系数向量β的无偏差估计b为：

b=（X^TX）^-1X^TY （9-2-25）

用最小二乘法求得的响应面模型，是否真正反映响应量y与试验因素x之间统计规律性，是否可以作为实际响应的近似，必须通过方差分析和F检验才能断定。

众所周知，试验观察值y₁，y₂，…，y_n之间的差异是由两个方面的原因引起的：①自变量x取值的不同；②其他因素（包括试验误差）的影响。为了检验这两个方面的影响哪一个是主要的，必须把它们所引起的差异从变量y的总差异中分解出来。n个试验观察值之间的总差异可以用试验观察值y_i与其算术平均值y的偏差平方和来表示，称为总的偏差平方和。记为：

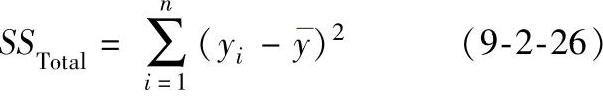
对其进行分解可得：

SS_Total=SS_Model+SS_Error （9-2-27）

式中，SS_Model为响应面模型偏差平方和，由自变量x的变化引起，其大小反映了自变量x的重要程度。SS_Error为剩余偏差平方和，由试验误差以及其他因素引起，其大小反映了试验误差以及其他因素对试验结果的影响。

响应面模型偏差平方和的计算表达式为：

因此，剩余偏差平方和的计算表达式为：

SS_Error=SS_Total-SS_Model （9-2-29）

总偏差平方和自由度的分解公式为：

f_Total=f_Model+f_Error （9-2-30）

式中f_Total=n^-1

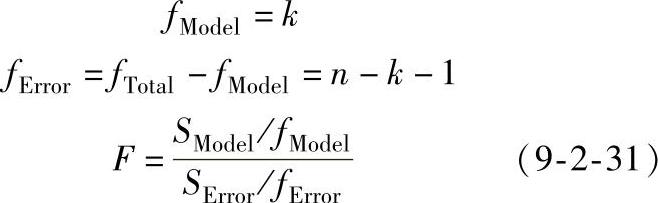
在原假设H₀∶β₁=0，β₂=0，…，β_k=0成立时，则：

F=F（k，n-k-1） （9-2-32）

因此，可用自由度为（k，n-k-1）的随机变量F进行检验。也可以使用指标R²（coefficient of multiple determination）、R²_a（R-square adjusted）判断响应面近似的质量：

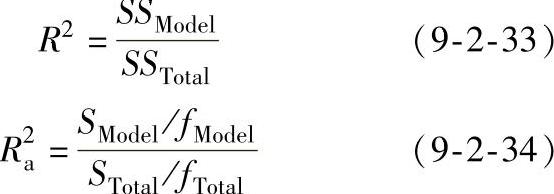
R²是完全拟合的度量值，反映响应面符合给定数据的程度，足够的逼近通常要R²的值在0.9以上。R²_a则更适用于评定响应面的预测精度。

响应面方程生成后，还须对其预测能力进行评估。可以根据已知响应的数据点，计算模型的预测值与已知值之差确定平均误差、均方根误差和最大误差，如果结果不能满足预设的精度要求，可考虑用更高阶的响应方程或增加试验设计次数；评估响应面时不能重复使用生成响应面的点。