人工神经网络：并行、稳健、自学习的记忆模拟系统

人工神经网络是一种大规模的分布式并行处理系统，它可以模拟人脑的记忆和联想功能，不需要了解过程的输入与输出参数之间的变化规律。通过对给定的样本数据进行学习，从大量的数据中提取规则，以一组权重系数的形式形成一种网络的稳定状态，然后通过联想记忆和推广能力来获取所需数据。人工神经网络的特点：并行性、稳健性、容错性和自学习能力。在人工神经网络中，神经元是最基本的处理单元，其数学模型如图9-2-1所示，其中X_ji为第j个神经元对第i个神经元的输入，W_ij为第j个神经元对第i个神经元的连接权值，θ_i为第j个神经元的阈值，f为传递函数，y为该神经元的输出。神经元的输入、输出关系如下：

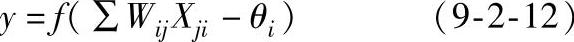
图9-2-1 神经元的数学模型

根据神经元之间连接方式的不同，人工神经网络分为：无反馈的前向网络和有反馈的前后向结合型网络。前向网络（见图9-2-2）由输入层、输出层和中间层（隐层）组成，中间层可以有若干层，每一层的神经元只接受来自前一层神经元的输出，一般不接受超越层次的输出。反馈型网络（见图9-2-3）的任意两个神经元之间都可能有连接，包括神经元到自身的反馈。在众多的人工神经网络模型中，以基于误差反向传播（Back Propagation，BP）的前向网络模型应用最广。

人工神经网络结构确定后，如何确定网络各神经元之间的连接权值是一个重要问题。对于非线性变换单元所组成的BP网络，变换关系是一个非线性连续可微函数，它可以严格利用梯度法进行推算，权的学习解析式十分明确。一般情况下，BP算法包含两个阶段。一是前向传播阶段，当给定输入量时，通过神经网络向前计算每一个神经元的输出，然后计算期望输出值T_j与实际输出值X_j之间的误差，均方差E表示为：

二是误差反向传播阶段，将误差从输出层向输入层的方向进行反向传播，以修正相应的连接权值，修正量可表示为：

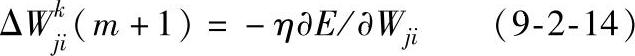
为了防止解的振荡，加一个惯性项。因此，新的权值修正量ΔW_j^ki可以表示为：

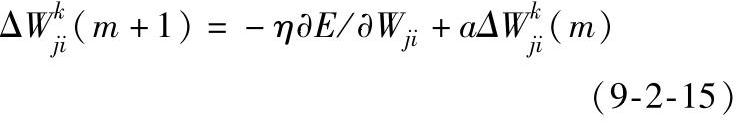
式中η——学习率；

a——动量因子；

m——迭代次数。(www.xing528.com)

图9-2-2 具有一层隐层的前向网络

图9-2-3 反馈型网络

神经网络学习的步骤如下：

1）确定BP网络的结构，即网络层数及各层神经元数量。

2）给出学习样本的输入、输出向量，如必要，则做归一化处理。

3）初始化，随机设置各层权系数和阈值。

4）向网络提供输入样本和理想输出值。

5）计算实际输出值。

6）计算误差。

7）若不满足误差要求，则返回继续学习；否则，则认为计算收敛。