正交试验法：设计多因子试验的重要方法

对于很多制造工艺，有时很难建立各工艺参数与质量或成本的函数关系，有时甚至还不清楚各工艺参数对目标的灵敏程度。因此，常采用正交设计的方法，进行试验设计DOE（Design of Experiment），从而发现质量或成本关于各参数的灵敏度，为设计优化奠定基础。

一般地，称影响试验指标的因素为因子，每个因子可能处的状态为水平。正交设计方法是一种研究多因子试验问题的重要数学方法，通过使用正交表进行整体设计、综合比较、统计分析。该方法的最大优点是可以从许多试验条件中完成最具有代表性的少数试验就能获得可靠的试验结果，即发现哪个因子的影响是主要的，哪个因子的影响是次要的。

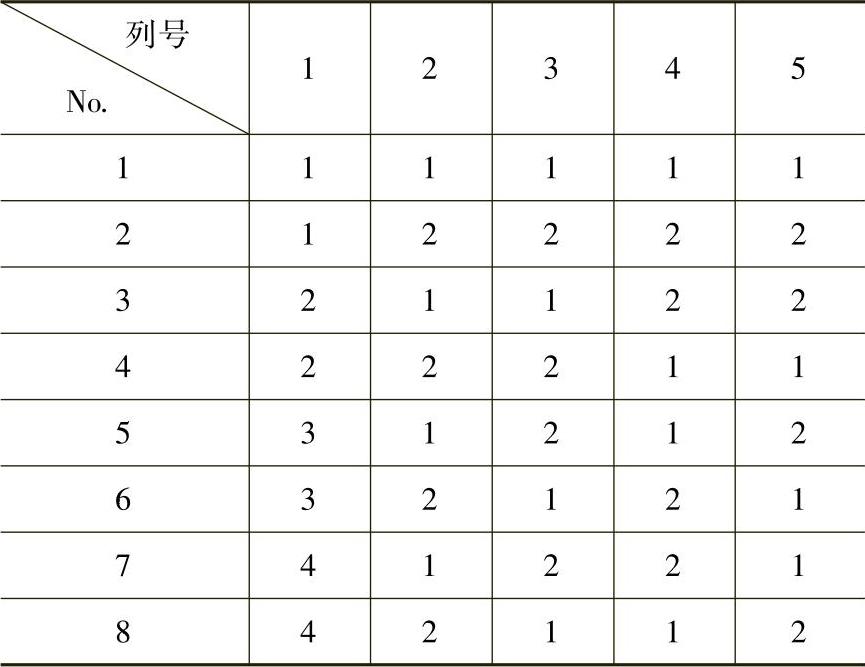
正交表是已经规范化的表，是正交试验设计的基本工具。最常用的是水平数相等的正交表和水平数不相等的正交表（也称为混合水平正交表）。正交表所共有的特性称为正交性，正是由于这种正交性，才使得用正交表安排的试验，具有均匀分散性和整齐可比性。如表9-2-1所示为一水平数相等的正交表L₈（2⁷）。其中L代表正交表；8为表的行数，即试验方案数；2为水平数，用数据1和2表示，7为列数，即因子数目。如表9-2-2所示为一混合水平正交表L₈（4¹×2⁴）。正交表的第一列为4水平列，用1、2、3和4表示，其余列为2水平列，用1和2表示。该表共有5列，即5个因子。当各因子间存在相互作用时，还需要使用正交作用表。

表9-2-1 正交表L₈（2⁷）

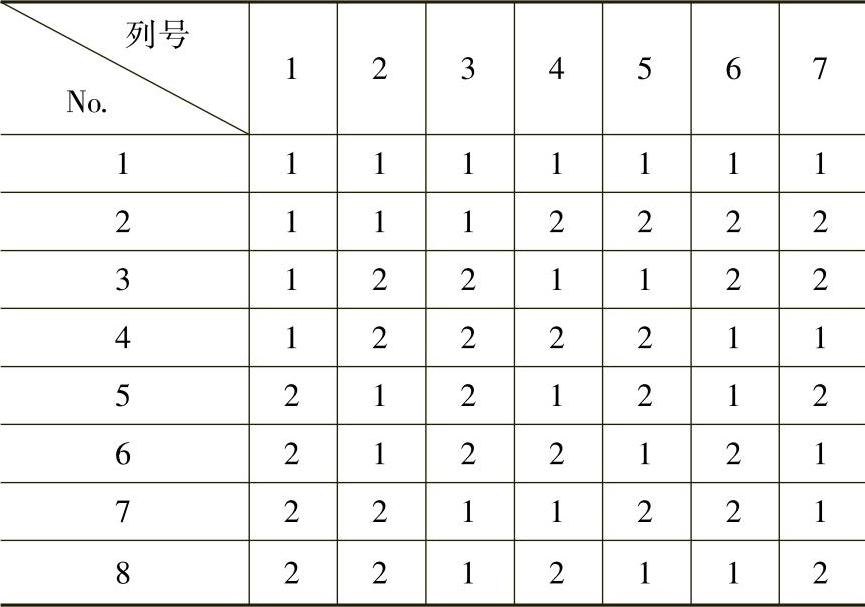
表9-2-2 混合水平正交表L₈（4¹×2⁴）

正交试验结果的分析可以采用直观分析或方差分析的方法。如表9-2-3所示为4因子3水平的正交试验的直观分析表。先计算出试验结果，然后根据极差的大小排序，极差越大说明该因子对试验结果的影响越大，该因素越重要。画出各因子与试验结果的关系图后，即可以看出各因子的水平值对试验结果的影响趋势，从而可以确定最佳的参数组合。(www.xing528.com)

表9-2-3 直观分析表

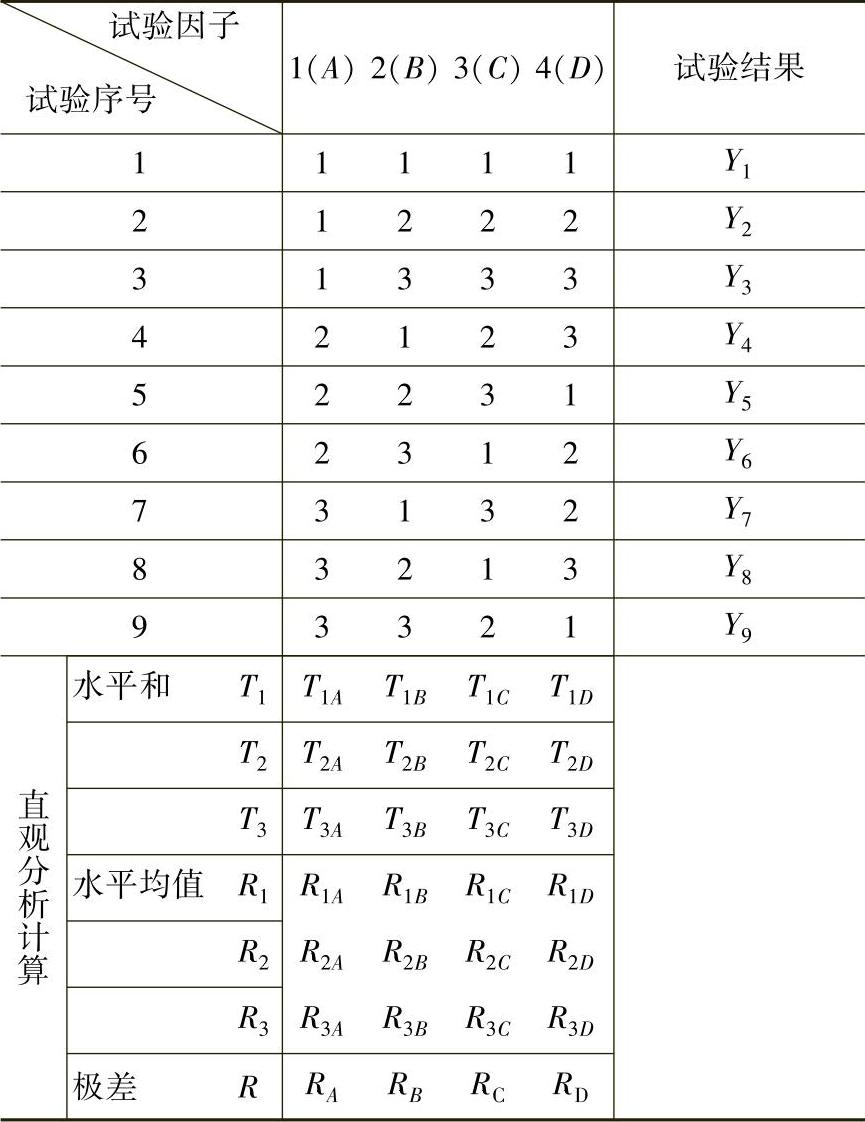
表中 T_ij——第j列水平值为i时的试验结果之和；i=1，2，3；j=A，B，C，D；R_ij=T_ij/N。

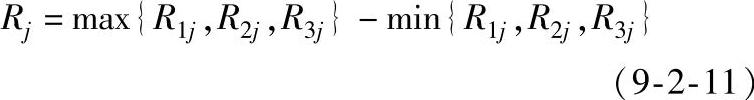
如果不考虑因素间的相互作用，则根据正交试验的关系图可找出最佳设计的水平，将各因素的最佳值组合起来即为参数的最佳组合。当需要考虑因素间的相互作用时，经过分析已知某两个因素的相互作用对试验结果影响很大，可把对应于这两个因素所有不同水平组合的试验结果进行比较，选出该两个因素的最佳水平组合，然后再综合考虑其他因素，确定最佳参数组合。

直观分析法简单、易于理解、计算工作量少、便于普及推广。根据正交表方差分析，可以定量地给出各因素影响的主次关系，此处不再赘述。