目前,锻造问题一般采用刚塑性有限元法求解。为清楚说明有限元法的基本概念和解题步骤,本节将通过简单介绍弹性有限元法引入一些基本概念,其中绝大部分内容将在刚塑性有限元法中用到。
等参数单元
所谓等参数单元是指单元内各点的位移(速度)和坐标用同样的插值函数表示。
将连续体离散化经常采用的二维单元有:平面三角形单元,四边形等参单元。
经常采用的三维单元有:四面体单元,六面体单元。
1.位移插值函数
在有限元法中,位移函数对精度有很大影响。单元的位移函数必须满足三个条件:
1)必须包括单元的刚体位移。
2)必须包含单元的常应变。
3)单元内的位移必须连续,相邻单元之间的位移必须协调。
条件1)和2)是有限元解正确性的必要条件,称为完备性条件;条件3)是充分条件,称为协调性条件。在有些问题中,满足协调性条件较为困难,可采用完备而不协调单元。
一个单元内各点的位移包括该单元自身变形引起的部分和由于其他单元变形通过节点传递给它的部分。后者即所谓刚体位移部分。
单元内各点处的应变包含着与坐标无关的常应变和与坐标有关的变应变两部分。当单元划分很小时,单元内的应变变化较小,常应变是主要部分。
变形后各单元之间的边界和节点不允许脱开。在单元内位移必须连续。
位移函数的确定可以采用两种方法。其一,是采用有若干待定系数的多项式,这些系数确定后就成为相应的节点位移参数。其二是采用形函数来描述,形函数通常是用插值多项式表示。位移函数除应满足完备和协调性之外,其待定系数的数目应和节点自由度数目相同,以便由节点位移唯一确定全部系数。以下以八节点平面等参数单元为例,说明插值函数的构造方法。
如图9-1-2所示为四边形八节点等参单元。该单元每边上有三个节点,位移函数在边上成二次曲线变化。位移函数写成:
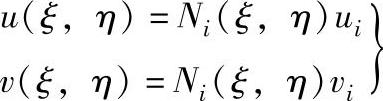
式中 Ni——针对具体单元和节点确定的多项式。
Ni的确定原则为:
1)Ni是坐标的双二次函数。
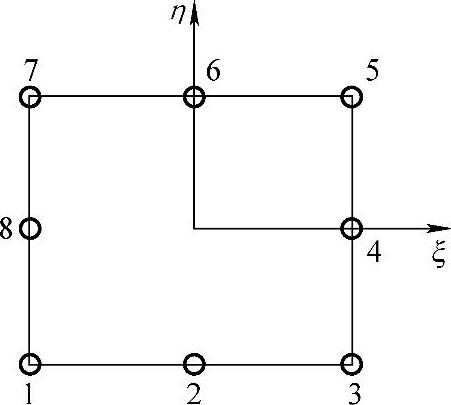
图9-1-2 四边形八节点等参单元
2)Ni在节点i等于1,在其余的节点,Ni=0。即:
Ni(ξi,ηi)=1,Ni(ξj,ηj)=0(i≠j)
下面以N1(ξ,η)为例说明建立方法。在节点2-8上,Ni(ξ,η)=0。三条直线 ,
, ,
, 通过7个节点,方程式为:
通过7个节点,方程式为:
ξ-1=0,η-1=0,ξ+η+1=0
多项式(ξ-1)(η-1)(ξ+η+1)在节点2-8为0。再利用N1(ξ1,η1)=1的条件,有:
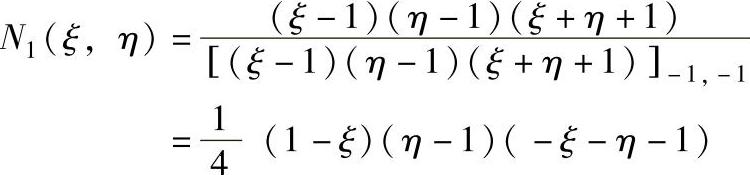
同样可以得到:
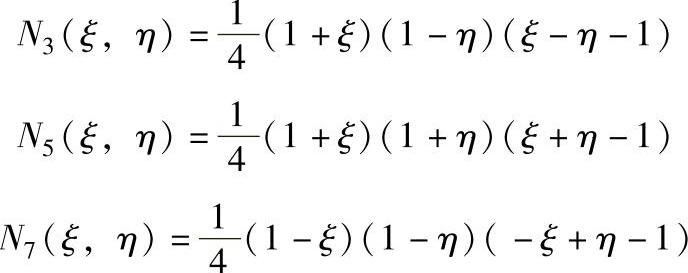
再求N2(ξ,η),N2(ξ,η)在节点1,3-8为0。直接 ,
, ,
,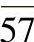 通过7个节点,方程为:
通过7个节点,方程为:
ξ+1=0,ξ-1=0,η-1=0
多项式(ξ+1)(ξ-1)(η-1)=(ξ2-1)(η-1)在上述节点为0。再利用N2(ξ2,η2)=1的条件,有:
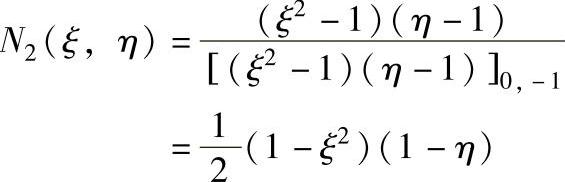
同样可得:
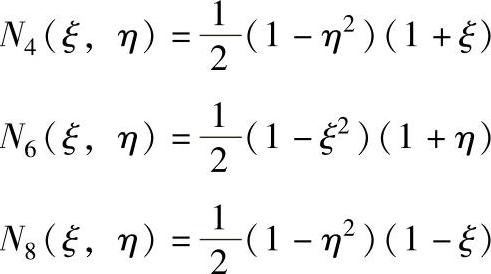
注意到8个节点的局部坐标系,可以得到统一表达式为:
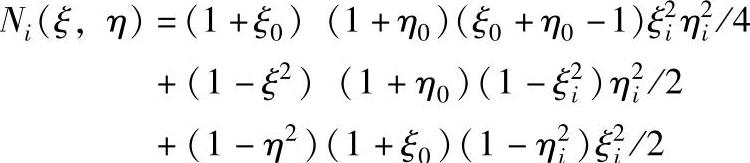
式中ξ0=ξiξ,η0=ηiη。局部坐标系和整体坐标系间的变换关系为:
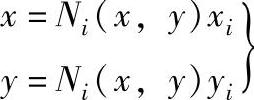
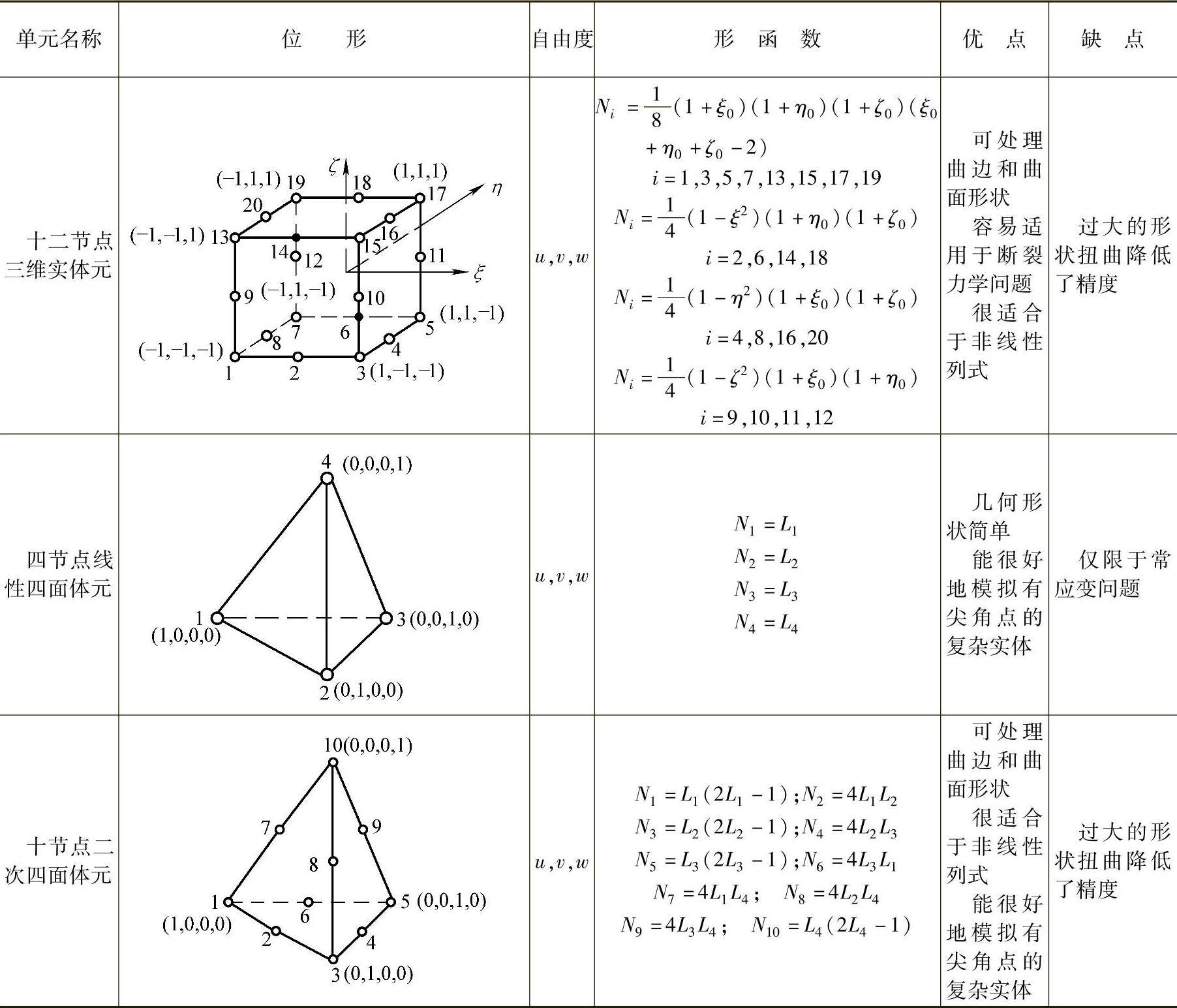
表9-1-1和表9-1-2分别列出了锻造过程中可能用到的平面等参数单元和三维等参数单元。
表9-1-1 常用平面等参数单元
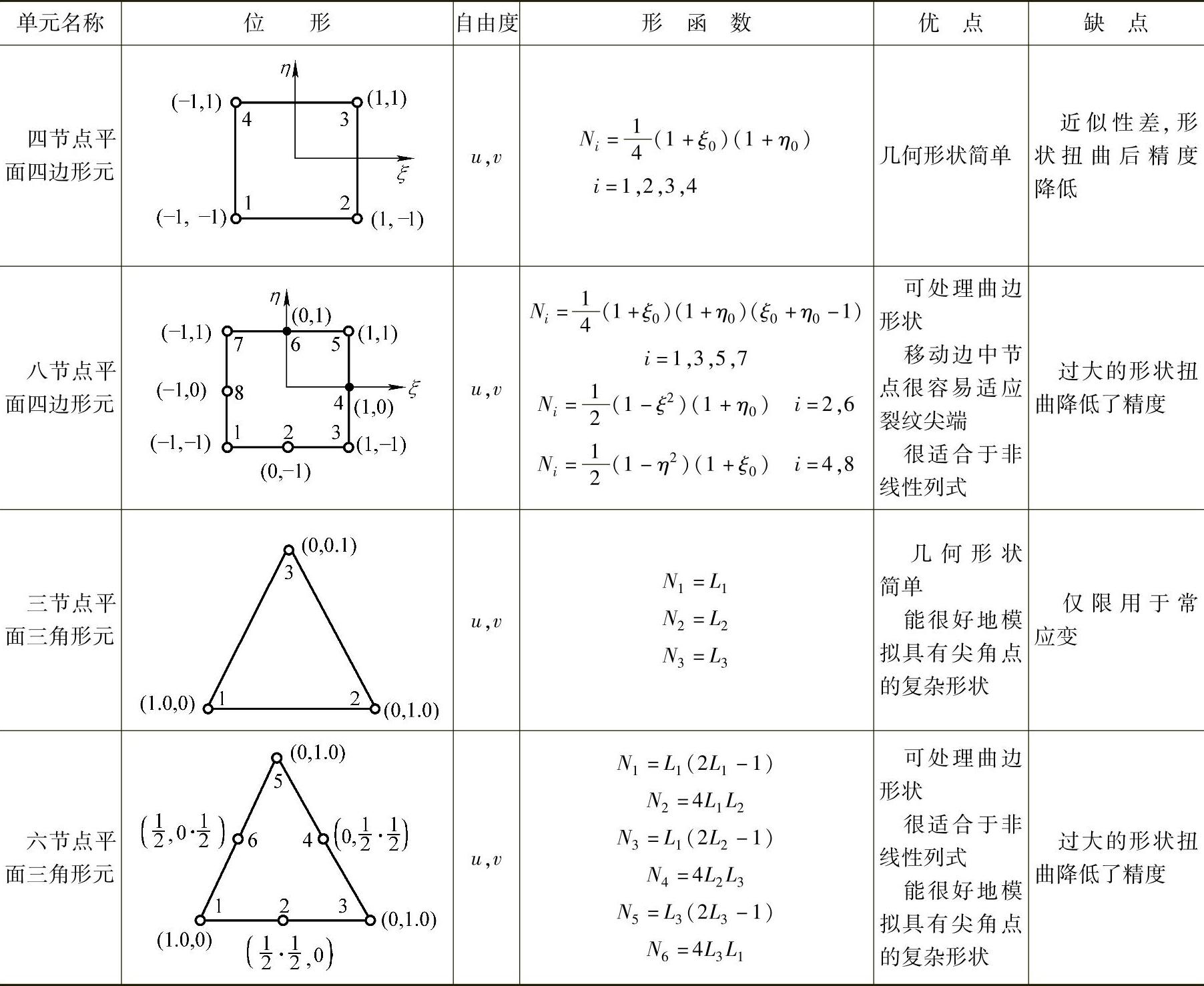
表9-1-2 常用三维等参数单元

(续)
2.应变速率—位移速度矩阵
(1)三维固体等参数单元的应变—位移矩阵 三维固体8节点6面体等参数单元的应变速率和位移速度关系为:

式中 B——应变速率矩阵,其元素为:

其中
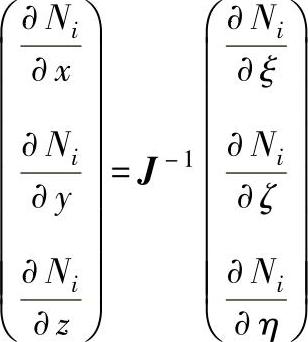
式中 J-1——雅可比矩阵的逆矩阵。
雅可比矩阵的表达式为:
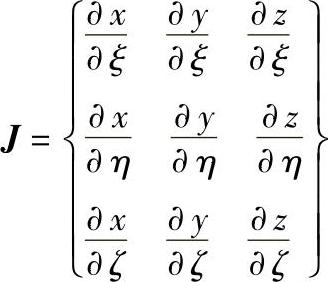
(2)平面固体等参数单元的应变速率—位移速度矩阵 以8节点4边形单元为例,按照应变速率与位移速度的关系和位移插值函数的定义,平面问题的应变速率表达式为:
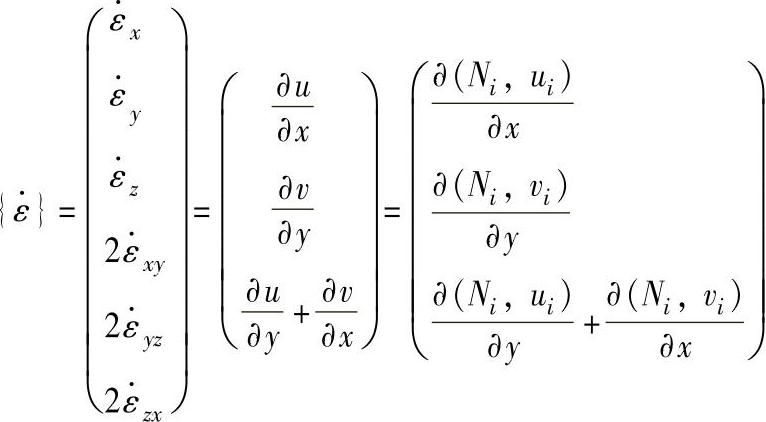
轴对称问题的应变速率表达式为:

记
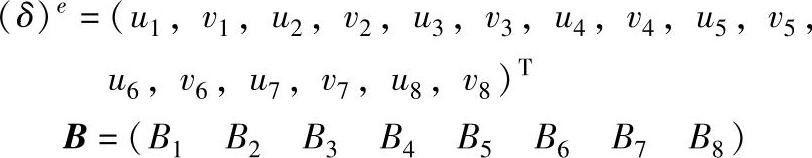
平面问题的B矩阵为:

轴对称问题的B矩阵为:
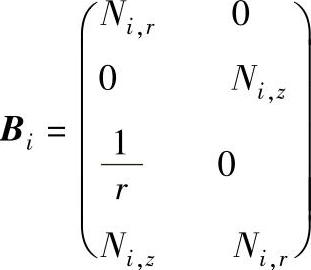
式中 Ni,x等代表形函数对各坐标求偏导数。
则有:
{ε}=B{δ}e
式中 {ε}——应变向量;
{δ}e——节点位移向量;
B——应变—位移矩阵,通常简称B矩阵。
但是,B矩阵中Ni是局部坐标的函数,因此还要进行转换。由复合函数求导,有:
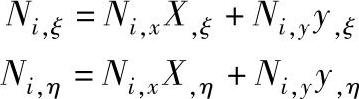
写成矩阵形式,有:
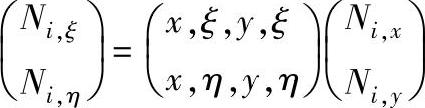
记雅可比矩阵为:
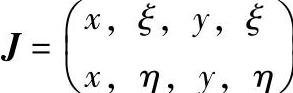
则有:
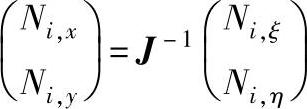
雅可比矩阵的逆阵为:
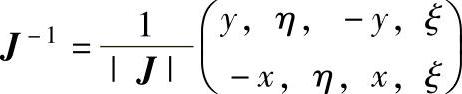
式中|J|——雅可比矩阵的模。
矩阵的各元素可以通过插值函数对局部坐标的导数和节点坐标得到:
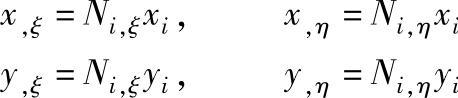
按照形函数的统一算式,有:
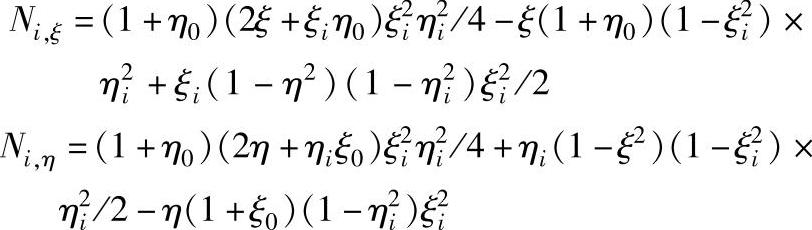
3.单元刚度矩阵
虚功原理是最基本的能量定理,它是用功能的概念来表示平衡条件。
虚位移是指假定的、微小的、满足约束条件的任意位移。它不是结构实际产生的位移。满足约束条件是指虚位移应满足变形协调方程和位移边界条件。任意性是指满足约束条件下的可能位移,与结构受载荷状态无关。
外力虚功是指作用在结构上的外力在虚位移上所作功。由于外力作用也会产生弹性体各单元的虚应变。虚功原理可以表述为:在外力作用下处于平衡状态的弹性体,当发生约束允许的任意微小虚位移时,外力在虚位移上所作功等于弹性体内的应力在虚应变上所作的功。
假设弹性体的所有节点都产生虚位移,以四边形八节点等参单元为例,虚位移向量可以表示为:
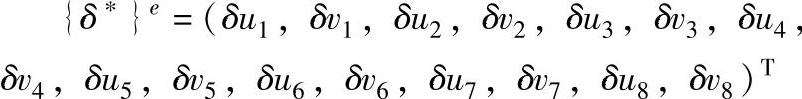
单元内的虚应变为:
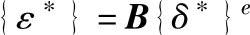
于是外力R在虚位移上所作功为:
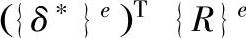 (https://www.xing528.com)
(https://www.xing528.com)
单元内的应力在虚应变上所作功为:
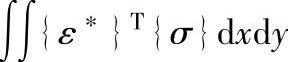
此处假设单元的厚度为单位厚度。将应力和应变的矩阵表达式带入上式,并将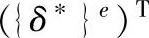 提到积分号前,整理后有:
提到积分号前,整理后有:
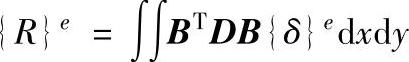
记
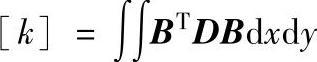
再由
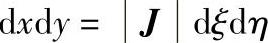
有
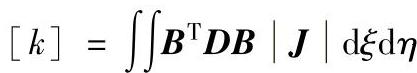
即将刚阵转化为对于局部坐标的积分。
[k]称为单元刚度矩阵,可以写成分块表示,对于本单元可分成64块2×2的子矩阵
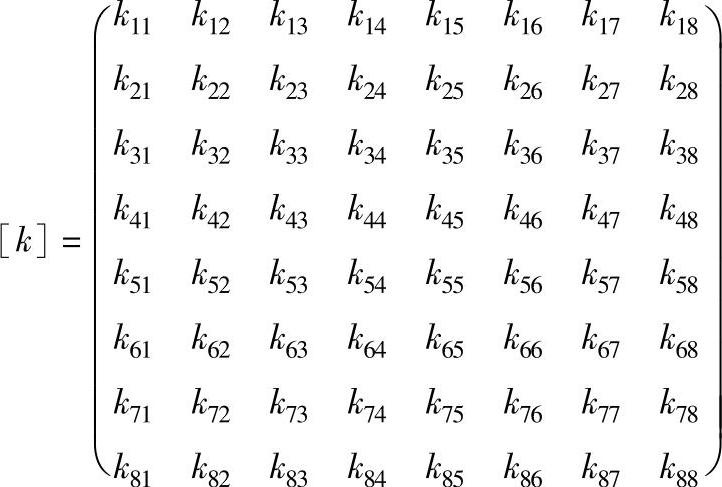
其中每个子矩阵的算式为:
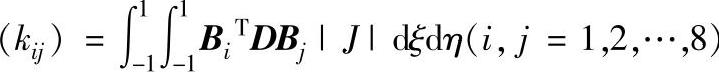
单元的节点力和位移的关系可以写为:
{R}e=[k]{δ}e
4.等效节点力向量
单元所承受的载荷主要有集中力、体积力和表面力三种形式。
(1)集中力向量 设单元内任意一点c受有集中力{F}=(FxFy)T,移置到节点上的等效节点力按下式计算:
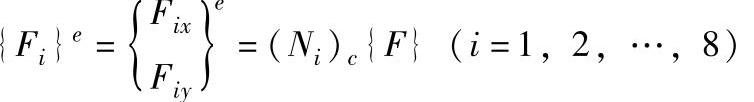
式中 (Ni)c——形函数Ni在载荷作用点上的值。
确定载荷作用点的方法是,给定该点的整体坐标,如(xc,yc),有:
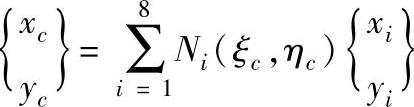
通过上式可以解出载荷作用点的局部坐标(ξc,ηc),即可求得(Ni)c。如果集中力作用在节点上,则可不必进行载荷移置。
(2)体积力向量 设单元的单位体积力为{G}=(GxGy)T,移置到节点上的等效节点力按下式计算:
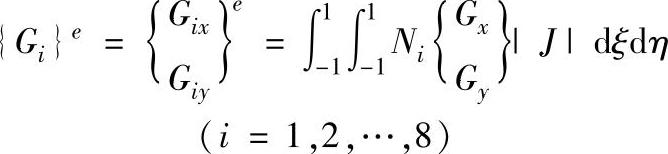
(3)表面力向量 设单元某边上受有单位表面力{P}=(PxPy)T,移置到这条边的三个节点上的等效节点力按下式计算:
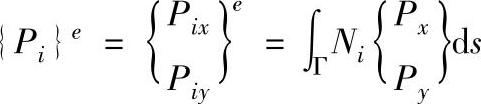
式中 Γ——受有表面力的单元边界;
s——弧长。
但是通常给出的是沿曲线边界的切向力和法向力{P}=(PnPt)T,如图9-1-3所示。假设单元的η=1边为受力边界。按本书的规定,该边的三个节点沿逆时针方向依次为5,6,7。再设定如图所示方向的力符号为正,反之为负。微段ds上所受力dF在x,y方向上的分量为:
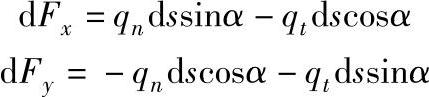
由
sinα=dy/ds,cosα=dx/ds
有
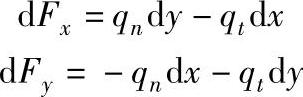
转为局部坐标,在η=1边上
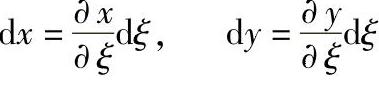
于是
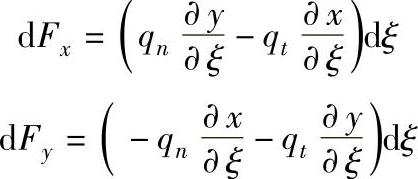
因此对节点i,单元的等效节点载荷为:
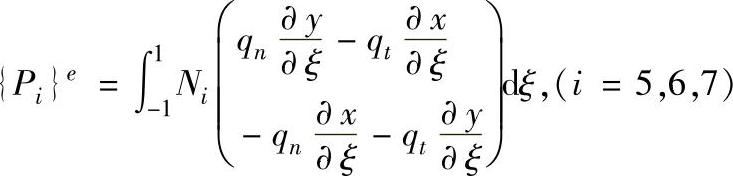
如若载荷作用在单元的其他边上,也可通过类似推导得到。
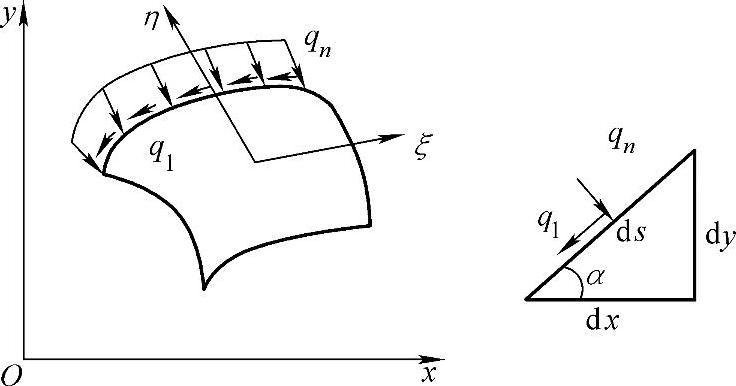
图9-1-3 表面力示意图
5.整体刚度矩阵的集成
假设结构划分为m个八节点四边形平面等参数单元,有n个节点。则整体的节点位移列阵为:
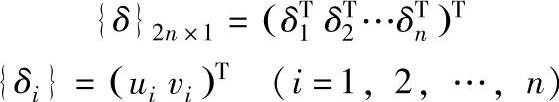
式中 {δi}——节点i的位移向量。
整体的节点载荷列阵为:
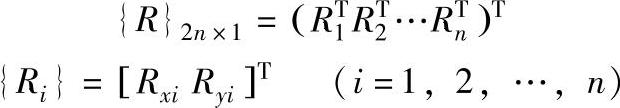
式中 {Ri}——节点i的等效节点载荷向量。
将各单元的节点载荷向量扩大为2n×1阶向量
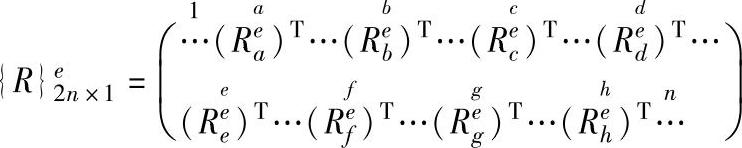
这样扩大后的各个单元的{Ri}e=(RxiRyi)T
载荷列阵可以相加,叠加在一起便形成整体载荷列阵。叠加以后相邻单元之间的结构内力产生的节点力可以相互抵消,只剩下外载荷引起的节点力。
将单元刚度矩阵扩大为2n×2n阶方阵。

单元的能量方程为:
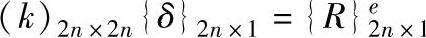
单元刚阵中,除了64个子矩阵之外,其余都为0,所以上式中可以采用整体的位移列向量。将上式对m个单元求和,可得到:
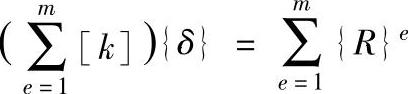
式中 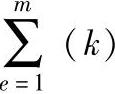 ——总体刚度矩阵,通常记为[K]。
——总体刚度矩阵,通常记为[K]。
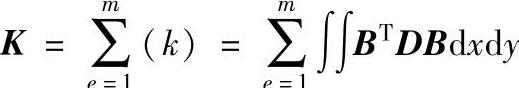
整体刚度矩阵可以写成分块矩阵的形式,每一个子块为:
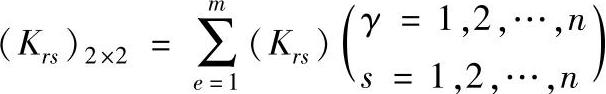
它是单元刚度矩阵扩大到2n×2n阶之后,在同一位置上的子矩阵的和。由于单元刚阵扩大后,很多子矩阵为0,所以只有当子矩阵的下标为r或s时,子矩阵才不为0。
最后可以写出整个结构的能量平衡方程:
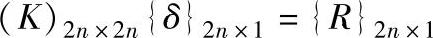
上式实际是由2n个方程组成的线性方程组。
6.位移边界条件的处理
处理位移边界条件较常用的有3种方法:消行消列法;整体刚阵对角线元置大数法和整体刚阵对角线元置法。第一种方法要修改刚阵在计算机中的存储,第二种方法的计算精度受所置大数的影响。第三种方法较为常用。
第三种方法保持着整体刚阵的阶数不变,只修改整体刚阵和载荷向量。如当节点i在y方向的位移vi为已知,则令总体刚阵中的对角线元素k2i,2i为1,而第2i行和2i列的其余元素均为0。总体载荷向量的第2i行元素用vi带入,其他行元素均减去vi和总刚阵修改前该行相应列元素的乘积。
举只有四个方程的例子:
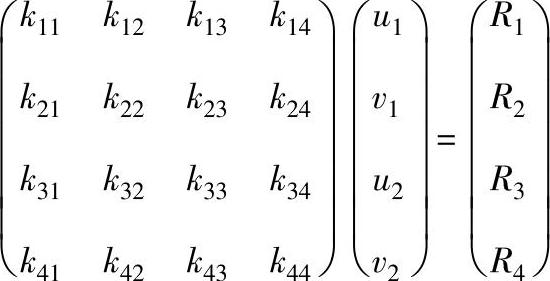
注意上式中kij为单个元素,并非子阵。设位移已知条件为:
u1=α1,u2=α2
按上述方法处理后,方程成为:
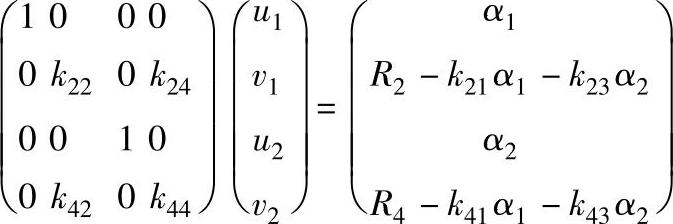
该方程的解显然满足u1=α1,u2=α2的位移已知条件。
7.高斯积分法
单元刚度矩阵和等效节点力的计算要遇到如下形式的积分:
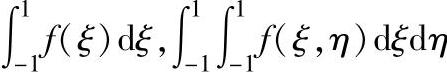
被积函数通常很复杂,不能进行显式积分。因此经常采用数值积分。一般在单元中确定积分点,算出被积函数在这些点的值,再乘以加权系数后求和,作为近似积分值。
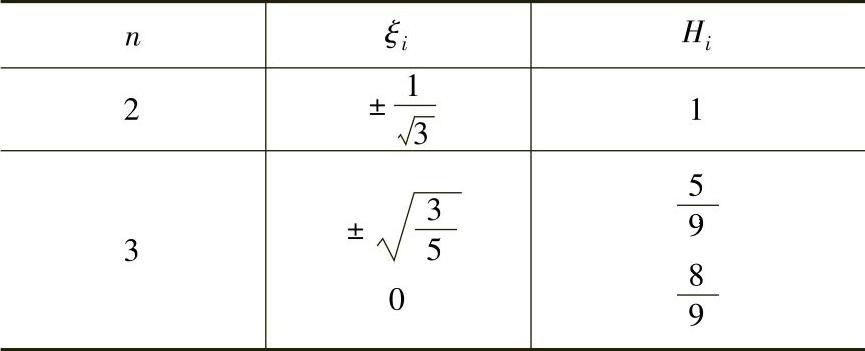
一维高斯积分公式为:
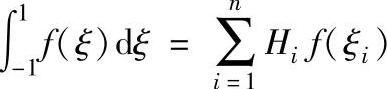
式中 n——高斯积分点数;
ξi——积分点i的局部坐标;
Hi——加权系数(见表9-1-3)。
表9-1-3 高斯积分公式的积分点坐标和加权系数
积分点数目与被积函数多项式的次数有关,当被积函数为m次多项式时,n≥(m+1)/2。计算量将随n的增加而剧增。
二维积分公式为:
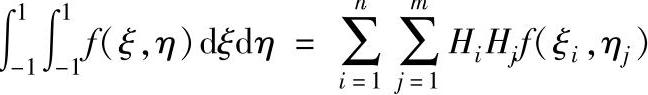
具体到八节点四边形等参单元,由于被积函数为3次多项式,则表面力的等效节点力的积分可采用n=2或n=3;平面单元刚阵的积分可采用2×2或3×3积分。体积单元的表面力可采用2×2或3×3积分,刚度矩阵可采用2×2×2或3×3×3积分。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




