径向锻造身管膛线的数值模拟优化方案

径向锻造技术作为身管膛线制造的一种方法，由于有残余压应力的存在，可以提高身管强度。采用传统力学解法很难得到身管膛线精锻成形过程中金属材料流动的信息，而运用有限元技术对锻造成形过程进行仿真模拟分析成形过程，可以有效地预知成形过程中的金属流动规律，变形特点及容易引起锻件缺陷产生的各种原因，以及在成形过程中模具各部分的应力、应变情况。

成形过程中金属的流动及变形特点对身管膛线质量影响很大，但由于对膛线成形过程中材料流动情况进行观察和实验研究比较困难，国内外学者基本上没有研究身管膛线的成形过程。国内有人利用有限元模拟软件Abaqus建立了三维轴对称的身管膛线精锻模型，对身管精锻工艺中膛线的成形过程进行了数值模拟，分析了膛线成形过程中影响膛线质量的材料流动嵌入芯轴过程中金属的流动情况、芯轴尺寸、成形角及断面收缩率对膛线成形效果的影响。

1.身管膛线加工有限元模型建立

有限元动力显式算法中的迭代时间与最小网格尺寸成反比，身管网格的尺寸对计算时间有很大的影响，枪管膛线深度尺寸较小（0.06～0.08mm），如果完全采用该尺寸范围内的网格，网格数目极为庞大，在现有的计算条件下无法进行计算，因此需要对网格进行疏密过渡。网格过渡方式主要分为径向过渡与周向过渡，过渡比例设为1∶2。其中径向过渡网格类型为六面体，周向过渡网格类型为六面体与五面体（三棱柱），并且径向过渡与周向过渡过程应当交错进行。过渡方式如图6-6-58a所示，采用疏密过渡后的网格数量大大减小，网格的质量依然符合计算精度的要求。

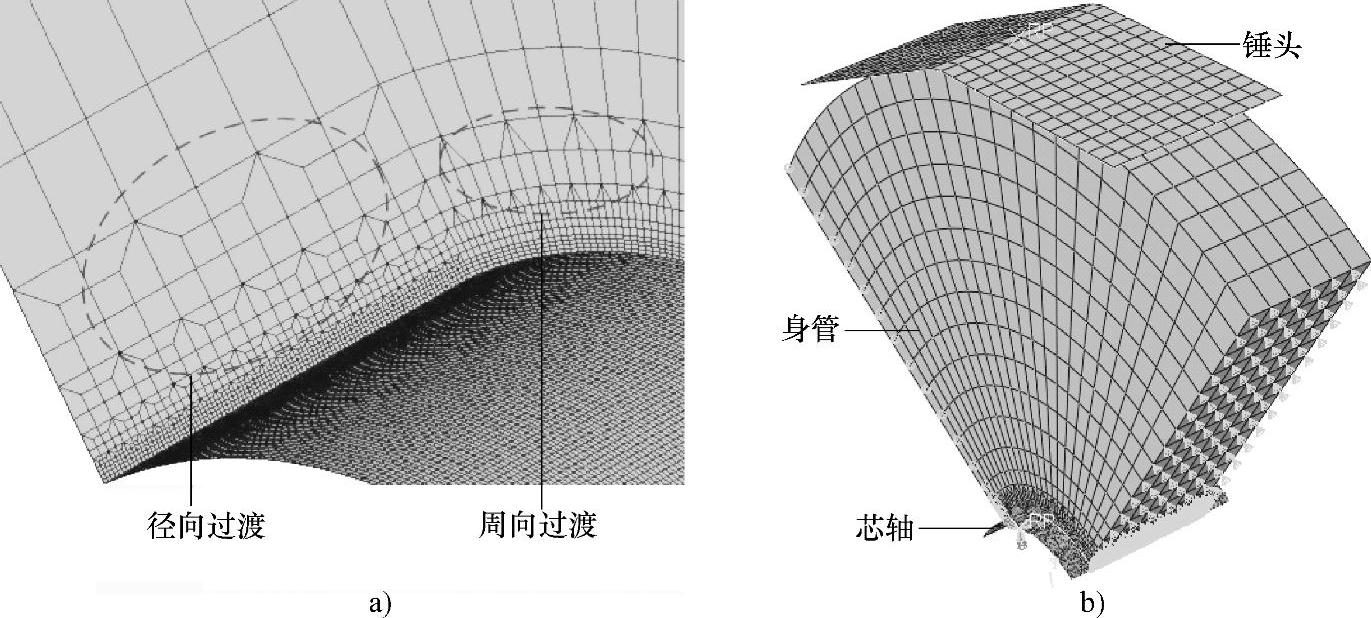
图6-6-58 膛线精锻有限元模型

a）网格过渡示意 b）整体模型示意

针对膛线成形过程中存在的几何非线性、材料非线性以及大变形等特点，选用商业有限单元软件Abaqus中的动力显式算法进行径向锻造过程的有限元建模。有限元整体模型如图6-6-58b所示，包括：锤头、身管和芯轴。截取身管的一段进行锻打研究，与实际尺寸有差别，但也可体现锤头接触身管到压入量达到最大时膛线成形金属流动情况。此外，不考虑锤头的压入角，即直接使用锤头的整形段对身管锻打。用于模拟的身管毛坯、芯轴膛线的基本几何尺寸见表6-6-7。考虑到径向锻造模型的对称性，选用1/4模型进行模拟。身管单元类型选择带有沙漏控制的减缩积分单元C3D8R，由于身管径向锻造工艺属于大变形过程，使用ALE网格自适应功能可使工件网格在变形过程中保持良好的质量。锤头、芯轴设置为刚体，单元类型选择四节点刚性单元R3D4。

表6-6-7 用于模拟的身管和芯轴膛线的几何尺寸

身管材料为30SiMn2MoVA，考虑到所研究的径向锻造过程是在室温下进行，可以忽略温度及应变率对材料流变应力的影响。材料力学性能由拉伸试验得出，力学模型采用幂强化模型（σ=Kεⁿ），各参数见表6-6-8。

表6-6-8 身管材料力学性能

芯轴膛线有六条，导程305mm，右旋。在建立有限单元模型过程中需要定义两个接触对，即锤头与工件外圆表面的接触，芯轴与身管内表面的接触。在Abaqus中采用罚函数接触法定义各接触对间的约束，滑移公式选用有限滑移模型。此外，选用罚函数法来描述接触对间的摩擦行为，考虑到研究的径向锻造过程属于冷锻工艺，摩擦因数选用0.15。

径向锻造过程中锤头的运动符合正弦规律，考虑到所研究的径向锻造机器控制锤头运动的偏心棒的偏心距为3.5mm，且锤头的锻打频率为680次/min，因此锤头的运动方程为

y=3.5sin（0.0714t）

在该有限元模型中，身管周向的两个截面定义轴对称边界条件，即两个截面不存在周向运动，芯轴的六个自由度被完全限制。

2.身管膛线加工过程的金属流动情况分析

身管精锻工艺中阴线宽度a、阴线直径L₂、阳线直径L₁是膛线成形的三个最重要的指标，如图6-6-59a所示。在锻打时，毛坯的材料首先接触到芯轴外径，形成内膛阴线，然后在锤头力作用下，材料继续向阳线的空腔流动，形成内膛阳线，如果不充满，则内膛阴线宽度能保证，但阳线宽度就不能保证，如图6-6-59b所示，所以阳线成形是膛线锻打加工的重点。由于膛线结构为螺旋形，因此芯轴成形槽的中心与锤头的对称中心线所成的角度对膛线部分的金属流动有一定影响，国内主要研究了芯轴沟槽中心与锤头对称中心线重合时的金属流动情况。α是指在周向，膛线部分与中心轴线之间的夹角，如图6-6-59a所示。膛线部分（α的取值范围为-45°～45°）身管毛坯内层金属材料在不同时间段的径向流动情况如图6-6-60所示，考虑到身管毛坯内径比芯轴外径稍大，身管在锤头作用2.6ms后开始接触芯轴，在0～2.6ms内，身管材料径向流动较为一致，身管截面仍保持为圆形截面且身管厚度保持不变。

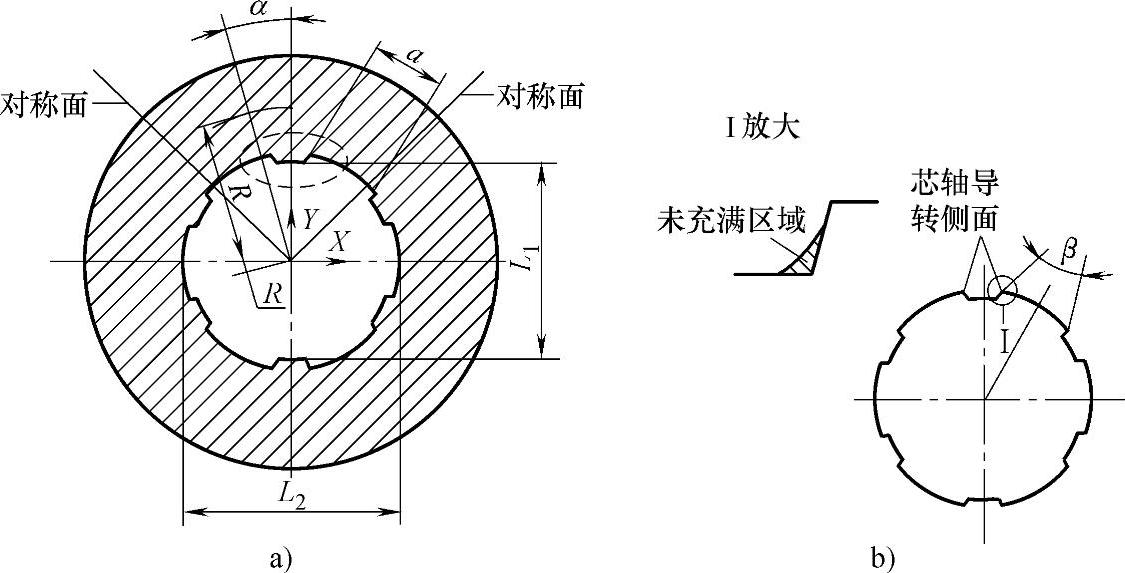
图6-6-59 身管纵截面示意及可能的缺陷

a）身管纵截面示意 b）芯轴纵截面及未充满区域示意(www.xing528.com)

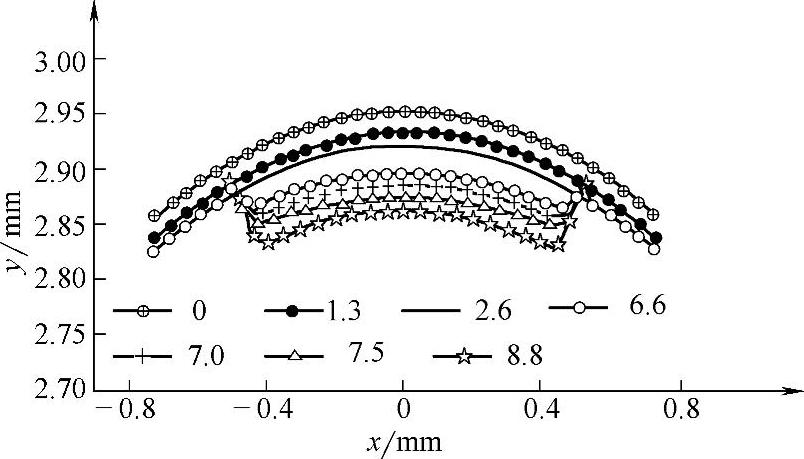
图6-6-60 身管毛坯内层金属材料在不同时间段的径向流动示意

身管膛线成形时间主要集中在第2.6～8.8ms，金属材料在嵌入过程中，与芯轴导转侧面（如图6-6-59b所示）接触部分的材料流动较为明显，膛线部分金属材料流动最快，此时金属材料沿着导转侧面逐渐流入芯轴的阴线槽内，而未接触部分的材料径向流动较为均匀，截面在锤头下压过程中依旧保持为圆弧形，此外观察身管阴线部分材料在锻打过程中周向流动并不明显，表明流入芯轴凹槽内的金属源于正对位置的身管部分，而芯轴凹槽两侧的金属很少流入到凹槽内；锤头下压时间超过8.8ms后，在第8.8～22ms时，锤头的能量主要转化为身管外圆直径的减小，但膛线内部仍然存在少量的金属流动，此后锤头的下压能量主要转化为身管外圆的材料流动。

锤头压入量达到最大值时身管内层（R=2.79mm）和靠近内层材料的流动随位置α变化的分布曲线如图6-6-61所示，定义金属材料顺时针流动为正。观察径向流动曲线，左右两侧近似于呈轴对称分布，45°对称面至身管阴线部分的金属材料在锻打过程中径向流动不明显，身管阳线部分金属在径向的位移曲线与芯轴形状较为相似；观察周向流动曲线，发现左右两侧近似于中心点对称，这是因为金属在精锻过程中可能向中心流动，因此左右两侧的金属材料在周向的流动方向相反，大小相等。45°对称面至身管阴线部分的金属中间部分的周向流动大于两侧，此外身管阴线附近的金属存在很小的周向流动，这是因为阴线附近金属需要流入到芯轴成形槽内。在芯轴的成形槽内，芯轴中心位置的金属材料几乎不发生周向流动，而其两侧的周向流动逐渐增加。

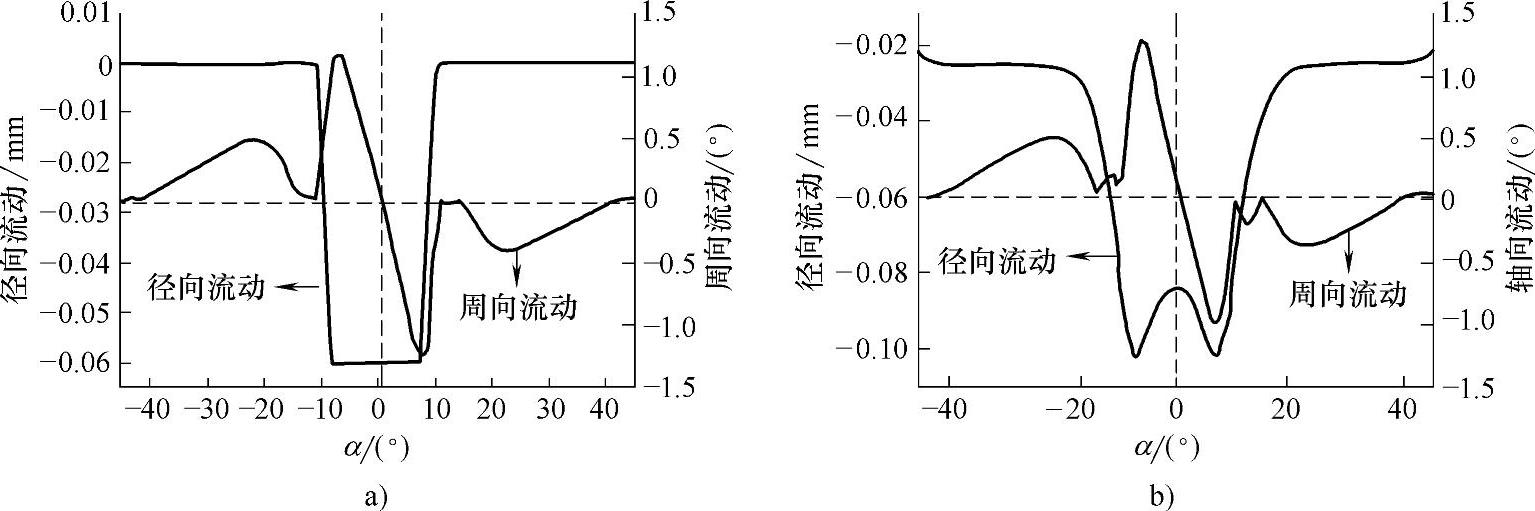
图6-6-61 身管毛坯内层金属材料流动分布

a）内层（R=2.79mm）金属流动分布 b）次内层（R=2.87mm）金属流动分布

当芯轴沟槽中心与锤头对称中心重合时，嵌入芯轴沟槽内的金属材料主要来源于正对于芯轴成形槽上方的金属，而身管阴线两侧的金属材料很少流入到芯轴槽内。有限元模拟膛线成形的结果如图6-6-62所示，虽然枪管阴线和阳线的高度差只有0.06～0.08mm，但所建立的有限元模型成功地模拟出了膛线的成形过程和结果。

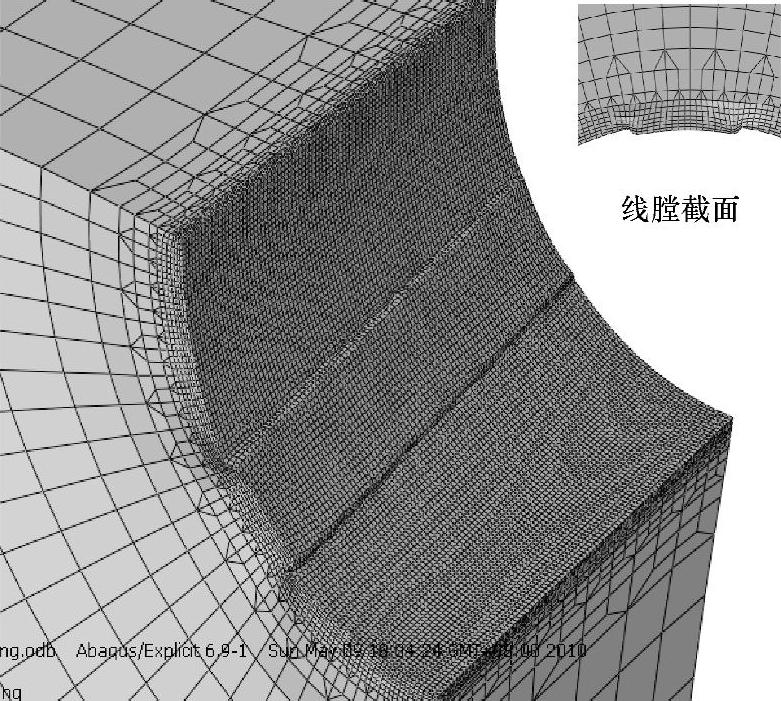
图6-6-62 身管膛线成形结果

3.芯轴成形角β及断面收缩率对膛线成形的影响

（1）芯轴成形角β对膛线成形的影响 芯轴成形角度β是指在芯轴纵截面内，芯轴任一膛线两侧面的夹角，如图6-6-59b所示。在锻打过程中，芯轴成形角度β过小易出现膛线无法充满等工艺缺陷。这里只分析不同芯轴成形角β对阳线宽度的影响。

分别计算β为-40°，0°，15°，30°，50°等五种情况下的身管膛线成形情况，选用最终成形后阳线宽度与设计尺寸的差值即成形偏差作为观察依据。不同β对应的膛线成形情况如图6-6-63所示。

图6-6-63 芯轴成形角β对膛线成形的影响

由图6-6-63可以看出，芯轴的成形角β对身管膛线的成形影响较大，成形角β越大，膛线成形效果越好。当β为-40°时，膛线成形较差，当β大于0°时，成形偏差随着β的增大逐渐减小。文中研究的产品中，所选择的芯轴成形角为30°。

（2）断面收缩率对膛线成形的影响 断面收缩率对身管精锻的成形影响较大，过小的断面收缩率会造成身管无法锻透，金属材料无法获得均匀致密的金相组织；断面收缩率过大又会造成锤头锻打力过大，加速锤头磨损，减少使用寿命。

模型采用改变锤头径向压下量的方式改变精锻模型的断面收缩率。不同断面收缩率对应的身管膛线成形偏差如图6-6-64所示。由图6-6-64可以看出，断面收缩率在20%～37%时，断面收缩率对膛线成形的影响比较显著，断面收缩率在37%～45%时，阴线宽度随着断面收缩率的增大逐渐接近设计尺寸，变化趋势逐渐趋于平缓。对于所研究的产品，断面收缩率选择在37%左右。

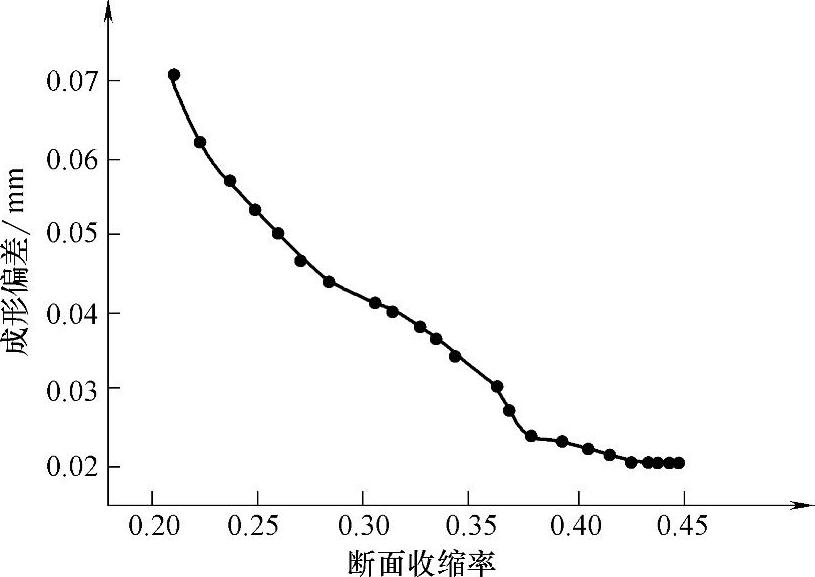
图6-6-64 断面收缩率对膛线成形的影响