径向锻造机变形力计算优化方法

目前尚无精确的计算公式计算三个以上锤头进行径向锻造时的变形应力和变形力。

一般公式的推导按下述假设进行。

1）径向锻造时的金属变形按轴对称问题考虑，并采用圆柱坐标系描述。

2）接触面边界满足Coulomb摩擦条件，接触面切应力与正应力成正比，即τ=μσ_s，μ为摩擦因数。塑性变形时接触面切应力达最大值，即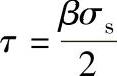，在轴对称问题中，系数β=1，σ_s为锻造温度下变形金属的流动极限。

3）在符合Coulomb摩擦条件时，锤锻面与自由表面的交界区，由于_μ很小，τ→0，塑性条件为：σ_max-σ_min=βσ_s，dσ_x=dσ_z。

（1）径向锻造机锻造棒料变形力的计算 锤头和工件的接触面呈圆弧面（如图6-6-29所示的径向锻造机锻轴时的受力情况），圆弧面中心角（锤头包角）为θ_d，圆柱面多向受压，径向锻造机有m个锤头则表示在m个方向受压。选用圆柱坐标系（ρ，θ，Z），从变形体内割取垂直于Z轴，距ρ轴为Z，宽dz的两个竖直面和接触面所包围的微分单元体（单元圆柱），接触面的弧长为。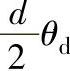

设径向锻造工件每锻一锤的最后直径为d，ρ轴

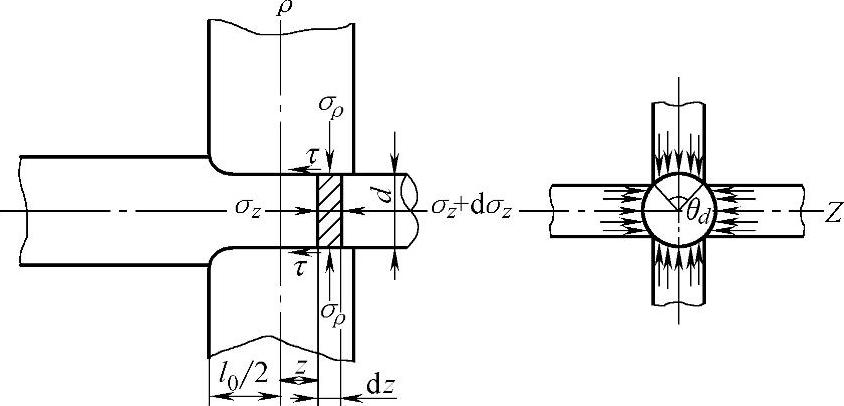
图6-6-29 径向锻造机锻轴时的受力情况

通过锤头中心线，σ_z在σ_z+dσ_z分别作用在ρ_θ面和ρ_θ+dθ^面上，设其为均布，ρ_θ和ρ_θ+dθ的面积均为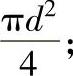

σ_ρ沿接触面θ_d（锤头包角）圆弧面均布，θ_d与锻件直径d的大小有关。

而θ_d圆弧边界面为自由表面，所以σ_θ=0。

考虑到在宽dz接触面上切应力τ的作用，可列出沿Z轴的近似平衡方程式：

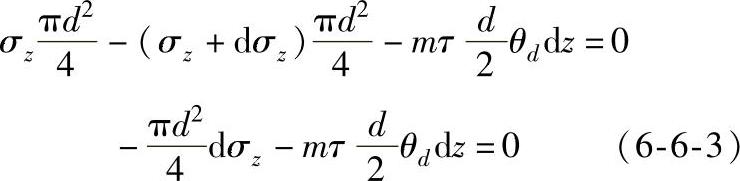
式中 θ_d——与直径d相对应的锤头包角（rad）；

m——锤头数。

简化上式，得到：

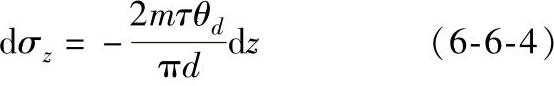
因为是轴对称变形，为了消除因假设σρ均为对单位流动压力的影响，将接触面切向应力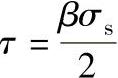代入式（6-6-4）中，得：

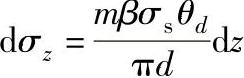
积分得：

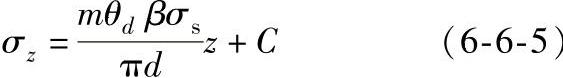(www.xing528.com)

当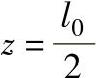（l₀为锤头宽度）时，σ_z=0，σ_ρ=βσ_s。

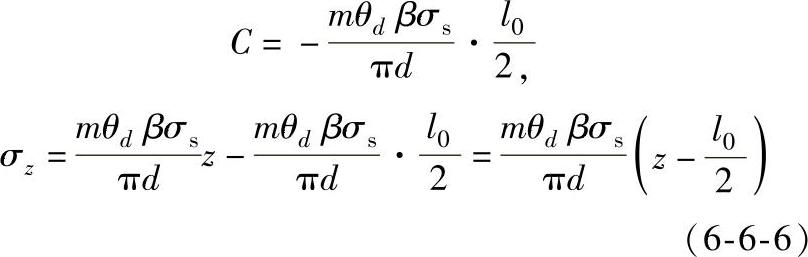
因为z值在0与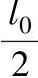之间，而σ_z为负值，所以式（6-6-6）要加一个负号。即为：

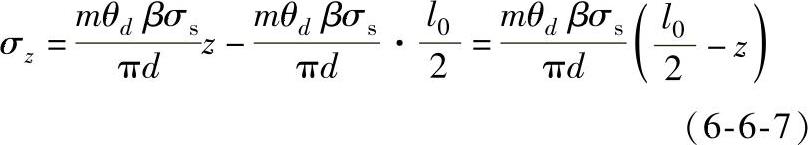
因为实际摩擦因数μ很小，τ→0。考虑到近似塑性条件，由于σ_θ=0，所以σ_max为σ_ρ，σ_z为σ_min，所以有：

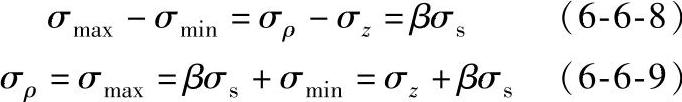
将式（6-6-7）代入式（6-6-9），得出锤击面正应力：

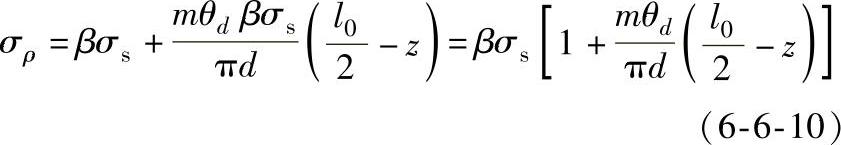
将σ_ρ沿压力平面积分求得变形力P，由于锤头宽度为l₀，所以

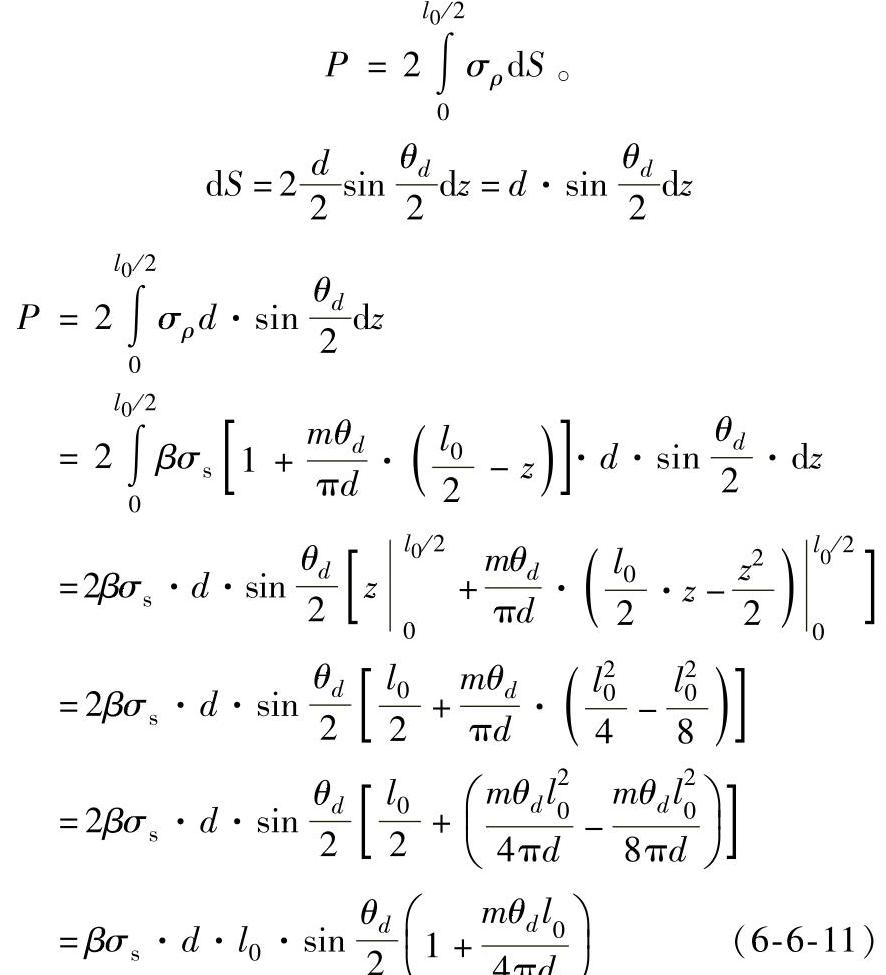
当β=1时，

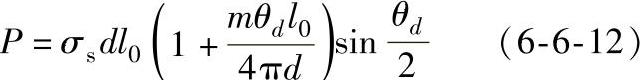
由式（6-6-11）和式（6-6-12）可见，径向锻造时的内在因素坯料的流动应力σ_s和外在因素锤头宽度l₀越大，P值越大。但在径向锻造过程中，锻造工件的最后直径d从坯料初始直径逐步变小到最后直径，锤头包角θ_d在每次锻造时都有所增大，对P值大小的影响不固定。

（2）径向锻造机锻造管料变形力的计算 某厂推荐计算中空管径向锻造锻打力的经验公式可以采用型砧下带芯轴延伸的变形力计算公式

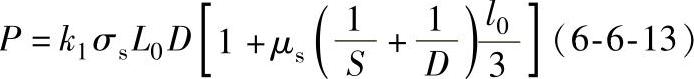
式中 σ_s——流动应力（MPa）；

L₀——砧长度，取锤头总长的40%（mm）；

D——锻件外径，取大头端外径尺寸（mm）；

μ_s——摩擦因数，取为0.5；

S——锻件壁厚，取大头壁厚（mm）；

k₁——与收缩率有关的系数，一次收缩率在3～4时，k₁取为1.05；一次收缩率在2～3时，k₁取为1。