摆头轨迹及其对摆辗运动的影响

摆头轨迹是指摆辗运动时摆头（也称摆杆）上端的空间球面轨迹。而模具上的一点在空间的轨迹与摆杆上端的空间轨迹是相似的，因此，模具与毛坯接触面积的位置变化规律与摆杆上端的空间轨迹也是相似的。研究摆头轨迹实质上研究接触面或成形区的轨迹。

摆头轨迹的水平投影可用图6-5-15b中矢量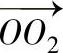的终点位置来表示，它是由内偏心套和外偏心套两个旋转运动而合成的。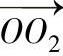矢量的矢径与极坐标的角度分别为

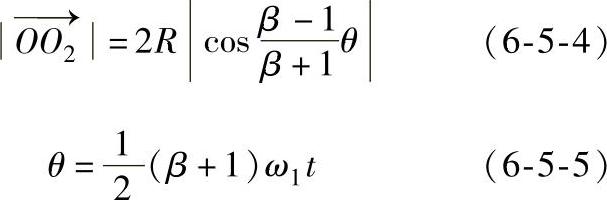
式中 β——角速度的比值;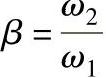

ω₁，ω₂——内偏心套和外偏心套角速度（rad/min）；

t——时间（min）。

根据角速度比值β的不同，摆头运动图形表现为五种形态，分别如图6-5-16和图6-5-17所示。

1）当β＞0且β≠1时，摆头运动图形为螺旋线型。

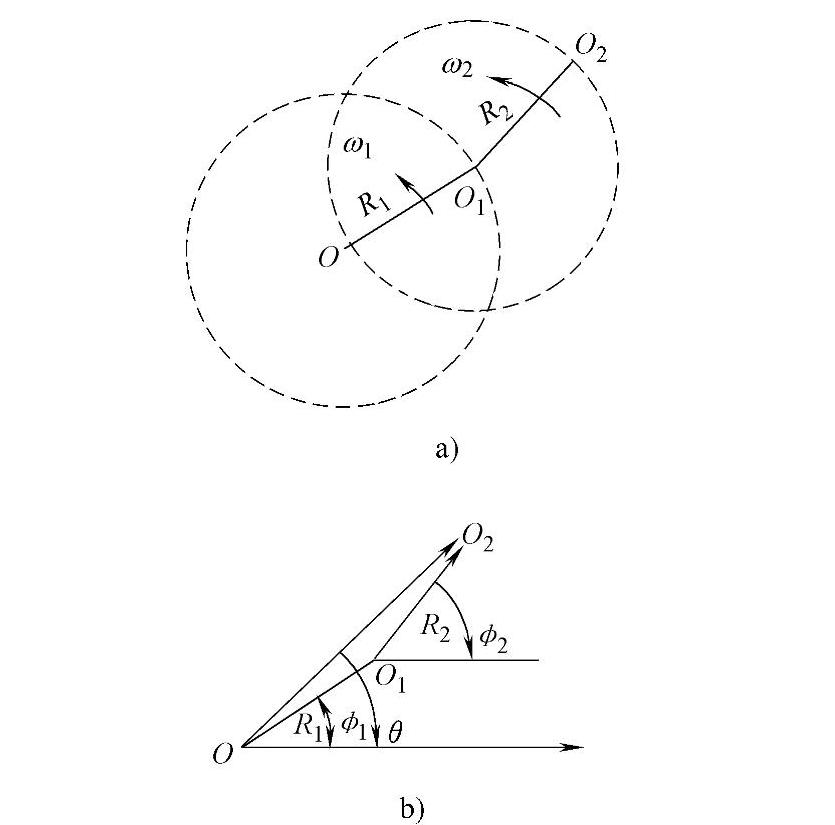
图6-5-15 摆头运动分析模型

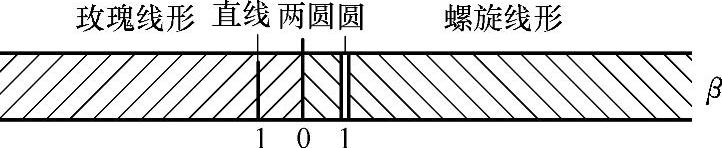
图6-5-16 摆头运动图形与β的关系(www.xing528.com)

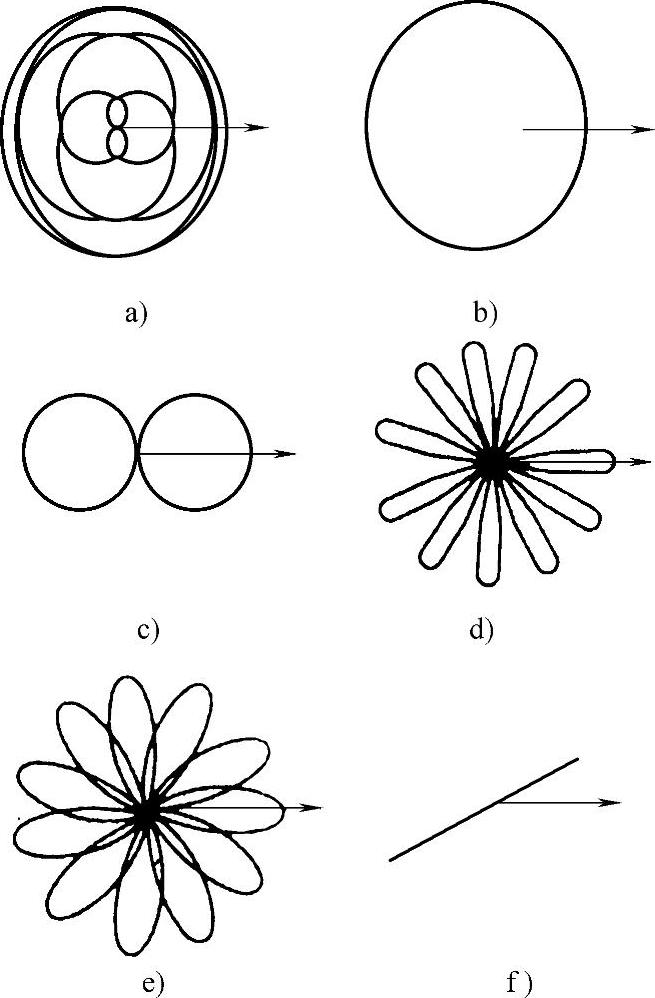
图6-5-17 摆头运动轨迹

2）当β=1，摆头运动图形为圆心在坐标原点的圆。

3）当β=0，摆头运动图形为圆心在（0，-R）、（0，R）处的两个圆。

4）当β＜0，且β≠-1，摆头运动图形为玫瑰线型。

5）当β=-1，摆头运动图形为直线。

圆轨迹时，摆头轴线与下模轴线始终保持为γ角，在均匀进给的情况下，接触面积率λ始终保持定值。成形力的合力作用点作等速圆周运动，因而，摆辗过程稳定且变形均匀。所以，圆轨迹对简单回转体摆辗成形特别合适。

玫瑰线轨迹时，摆头轴线与下模轴线的夹角在0～γ之间变动，接触区的大小、合力作用点都在发生周期性的改变，理论上存在“死区”。玫瑰线叶瓣数越多，则频率越高。因此，玫瑰线轨迹摆辗变形均匀性不及圆轨迹，同时还会使摆辗机产生较大振动。

螺旋线轨迹的摆辗变形特征介于圆轨迹与玫瑰线轨迹特征之间。

直线轨迹时，摆头作往复直线运动，始终只与直线区的毛坯端面接触，理论上特别适宜于齿条和直齿锥齿轮的摆辗成形。如果采用直线轨迹摆辗成形直齿圆锥齿轮，则下模需要装间歇转动装置，下模齿间要与直线轨迹准确对应，这给生产操作增加了难度，降低了生产效率，生产应用并无优越性。实际直齿锥齿轮摆辗成形生产中，通常都选用圆轨迹。

双圆轨迹与玫瑰线轨迹相似，存在“死区”，但变形不均匀性及摆辗机的振动小于玫瑰线轨迹。

无论是热摆辗成形还是冷摆辗成形，实际生产中都采用圆轨迹，其他轨迹并没有明显的实用优势。