【摘要】:粉末多孔体由于孔隙的存在,已不能运用连续体介质塑性力学。针对粉末体或多孔体的屈服问题,许多学者提出了不同形式的屈服准则。从图中可看出,当相对密度大于80%以上时,单向压缩时变形力小于等静压时的变形力,而变形能大于等静压时的变形能。
粉末多孔体由于孔隙的存在,已不能运用连续体介质塑性力学。由于粉末体塑性变形时体积的变化,可以假设为“可压缩的连续体”。针对粉末体或多孔体的屈服问题,许多学者提出了不同形式的屈服准则。其中,根据临界应变能概念导出的粉末多孔体屈服准则的一般表达式为:

式中 ReL——粉末体的下屈服强度;
J1——应力偏量第一不变量;
J2′——应力偏量第二不变量;
ν——粉末体的泊松比。
根据Kuhn和Downey给出的粉末体泊松比与相对致密度的关系式(5-5-1),考虑热变形时式(5-5-1)中的a值取2.0,得出屈服准则式(5-5-10)的另一种表达形式:

粉末体屈服准则在主应力空间是一个椭球面,其回转椭球的离心率仅是泊松比的函数:

由此可知,泊松比与相对密度关系是粉末体塑性理论的重要基础。与该屈服准则相关联的流动方程或本构方程为:
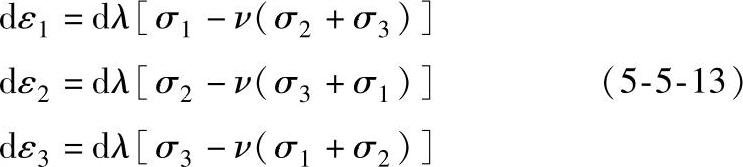
式中  (https://www.xing528.com)
(https://www.xing528.com)

式中 J2——应力张量第二不变量。
根据上述塑性理论,定性计算了无摩擦情况下圆柱体单向压缩和等静压致密时的力能参数变化规律,见图5-5-9和图5-5-10。从图中可看出,当相对密度大于80%以上时,单向压缩时变形力小于等静压时的变形力,而变形能大于等静压时的变形能。
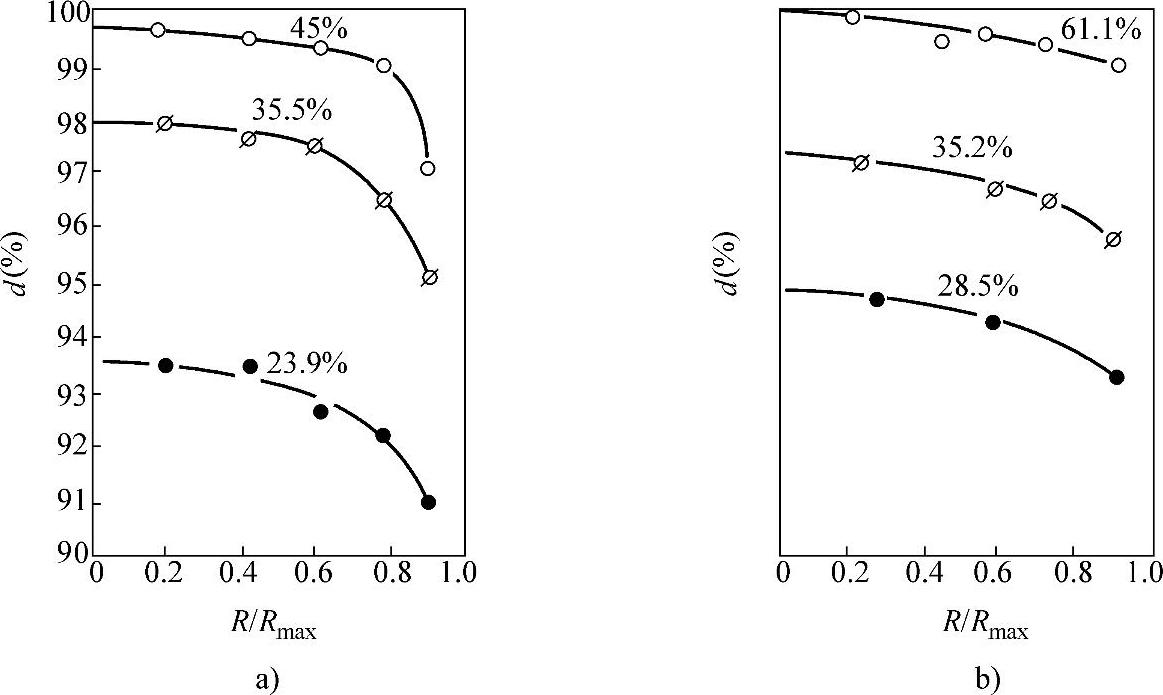
图5-5-8 601AB铝合金金圆柱体锻造时沿半径方向相对密度变化
(图中百分数为高度方向压缩率)a)无润滑 b)MoS2润滑

图5-5-9 单向压缩与等静压时的变形力比较
p1—等静压时变形力 p2—单向压缩时变形力 σ0—基体材料流动应力

图5-5-10 单向压缩与等静压时的变形能比较
WYS—单向压缩时变形能 WJY—等静压时变形能
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




