粉末体的泊松比与相对密度研究

体积可压缩性赋予了粉末多孔体一系列不同于致密体塑性变形的特征。多孔体的塑性泊松比与相对密度关系及塑性致密化方程，是这些特征的集中体现。

粉末多孔体塑性变形过程的体积变化，决定了粉末多孔体的塑性泊松比不再是常量（ν≤0.5）。Kuhn通过圆柱体单向均匀压缩实验给出了泊松比ν与相对密度d的简单经验关系式：

ν=0.5d^a （5-5-1）

式中 冷变形时，a=1.92；热变形时，a=2.0。

在粉末多孔体塑性变形致密化过程中，静水应力分量越大越有利于致密，塑性变形程度越大同样越有利于致密。多孔体塑性变形时的体积应变与静水压应力分量之间的对应关系，取决于多孔体塑性变形的应力状态与应变状态的对应关系，这表现在多孔体塑性理论中的本构关系。这里设多孔体塑性泊松比为：

设σ₁、σ₂、σ₃分别为多孔体应力状态的三个主应力，则主应力之比为：

β₁₃=σ₁/σ₃ （5-5-3）

β₂₃=σ₂/σ₃

根据多孔体塑性理论本构关系可以求出多孔体塑性应力状态与应变状态之间的对应关系：

式中 C=3d^a/（2+d^a）。

若在轴对称应力状态下，三个主应力分别为σ_r、σ_θ、σ_z（且σ_r=σ_θ），则有：

β=β_rz=β_θz=σ_r/σ_z，ν_rθ=ν_θz=ν^* （5-5-5）

根据式5-5-4和式5-5-5，则有：

ν^*=-3β-C（1+2β）/3-C（1+2β） （5-5-6）(www.xing528.com)

式5-5-6中ν^*即为轴对称情况下与应力状态相关的粉末多孔体的塑性泊松比。在式5-5-6中，当β=0即为单向压缩变形时的泊松比ν^*=-0.5d^a。根据式5-5-6可将轴对称情况下泊松比、应力状态与相对密度之间关系用图5-5-4表示出来。

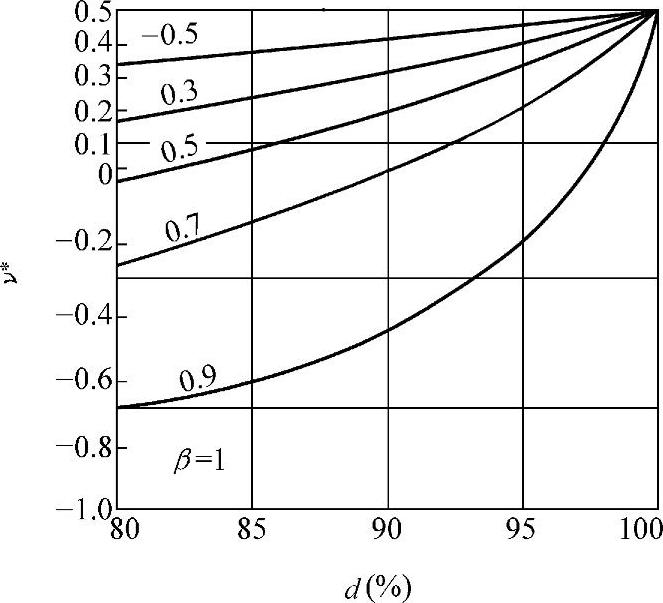
图5-5-4 ν^*-β-d三者之间的关系

当多孔体塑性变形时，根据质量不变条件，坯料的密度ρ变化由如下致密化方程确定：

dρ/ρ=-dε_V=-（dε₁+dε₂+dε₃） （5-5-7）

式中 dρ——对应于应变增量dε₁、dε₂、dε₃所产生的密度增量。

式5-5-7给出了密度增量变化dρ/ρ与体积应变增量dε_V之间关系式。若将式5-5-2代入式5-5-7，则可得任意应变状态下的塑性致密化方程：

dρ/ρ=-（1-ν₁₃-ν₂₃）dε₃ （5-5-8）

若由式5-5-6和式5-5-8可得出轴对称情况下的致密化方程：

dρ/ρ=-（1-2ν^*）dε₂ （5-5-9）

式5-5-9将粉末多孔体塑性致密与应力状态联系起来，可适应不同粉末体塑性致密化工艺。因此，可称式5-5-9为与应力状态相关的致密化方程。令q=（1+2β）/3=σ_m/σ_z用以表征静水压应力分量的大小，则可将式5-5-9用图5-5-5表示出来，从中可看出轴对称情况下，在不同静水压应力分量下变形程度对致密化速率的影响。

图5-5-5 不同静水压应力分量下变形程度对粉末体相对密度的影响

q=（1+2β）/3=σ_m/σ_z，当q=0.333对应于单向均匀压缩，当q=1.00时对应于等静压状态