上限法及其应用于速度场设计中的上限模式

1.上限法的基本概念与公式

上限法是由虚拟速度场和虚拟速度间断面入手，求解变形功率和变形力。该虚拟速度场满足速度边界条件和体积不变条件，称为动可容速度场（位移场）。上限法求得的近似功率和近似载荷均高于真实值，实质是一种高估法。但为了不过高于真实值，可对速度场进行优化，求出其极小值。

上限定理是上限法的理论基础。如图1-4-27所示，设变形体体积为V。表面分为两部分，即力面S_F和速度面（位移面）S_u。力面，即预先给定表面力的面；速度面，即预先给定位移速度的面。变形体内有速度间断面Γ。上限定理可表述如下：

在速度面S_u上，与任意动可容速度场u̇k_i对应的表面力T^k_i所做的功率，总是大于或等于真实表面力T_i在真实速度场u_i下所做的功率：

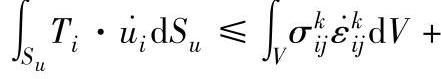
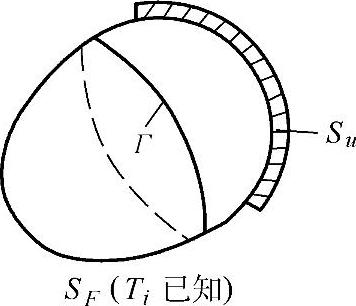
图1-4-27 边界条件与速度间断面示意图

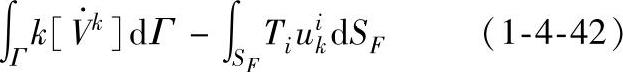
式（1-4-42）右端第一项为虚拟的连续速度场所做功率，第二项为虚拟的速度间断面上消耗的剪切功率，第三项为在力面S_F上，真实表面力和虚拟速度场所做功率，三项之和为所求近似变形功率。式（1-4-42）左端为真实功率。

考虑工具和变形体之间的摩擦力后，虚功率的计算式为：

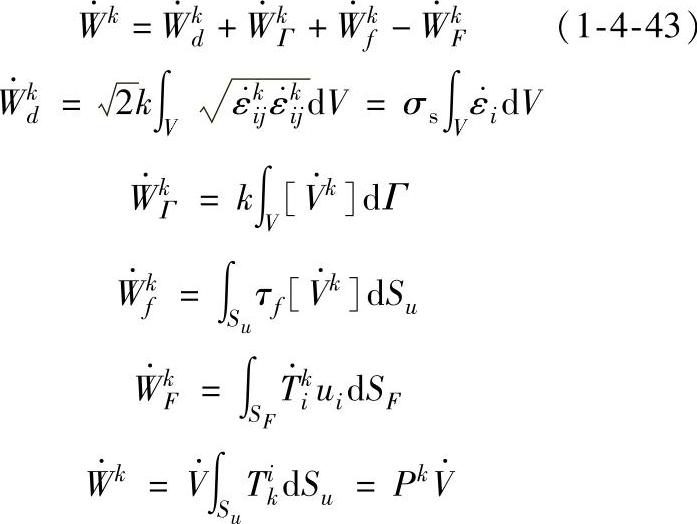
式中 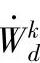——连续速度区消耗的功率；

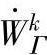——速度间断面上的剪切消耗功率；

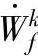——变形体与工具间摩擦消耗功率；

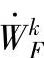——力面上表面力消耗功率；

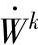——虚功率。

解题时，一般有下述两种情况。

（1）将变形体虚拟为由刚性块组成（工藤上限法）若将变形体视为由若干刚性块组成的，则各块内部并不消耗功率，即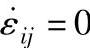，仅有各块间及刚性块与工具间的切应力消耗功率。此时：

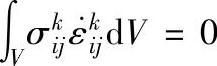
式1-4-43简化为：

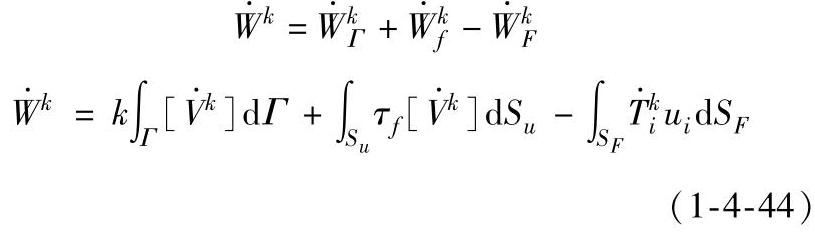
（2）塑变区虚拟为连续速度区与刚性区组成（Avitzur上限法）：

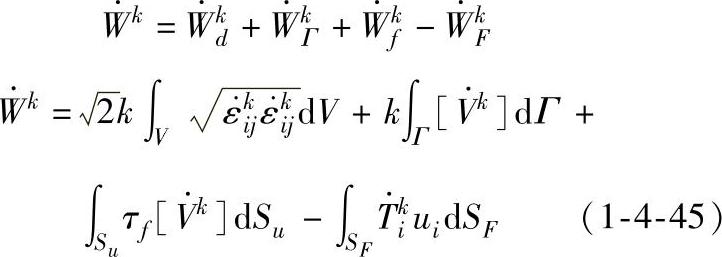(www.xing528.com)

2.上限模式及应用实例

（1）上限模式 上限法求解的关键在于设计速度场。设计速度场的不同类型通常称为上限模式，常用的有以下几种。

1）简化滑移线场上限模式（刚性块）。这种模式实际就是将连续的滑移线场简化为若干个刚性块，以此作为流动模式，求出间断面大小与速度间断值，用式（1-4-44）计算总变形功率，进而求出平均单位压力。

2）基元技术。在平面应变时把塑性区划分为若干个刚性块，称为“基元矩形技术”，每一矩形单位又由若干三角形组成。根据几何形状及摩擦状态确定矩形单元的流动模式，经优化后，求出单元的功率消耗系数e_i，从而求出整个变形体的总功率及工具的平均单位压力。对于轴对称问题，把子午面的塑性区看作由若干个矩形截面组成，每个矩形截面表示一个不同形状的圆环或圆柱单元，而矩形截面又由刚性块和连续速度区组成。这称为“基元圆环技术”。经过与基元矩形技术同样的步骤，可以求出总功率及平均单位压力。

3）连续速度场。这种模式是将变形体内的塑性区设计为连续的速度场，只有在刚塑性边界上产生速度间断。连续速度场的类型有：平行速度场、向心速度场及三角场等。设计上限模式，要依据变形体的几何形状摩擦状态，下面通过实例说明刚性块模式求解过程。

（2）断面收缩率为0.5的平面应变正挤压

图1-4-28是一种在铝合金型材制造中较为多见的典型的平面正挤压。图中上限模式是由4个相同的三角形组成的。三角形的数目越多，挤压力的上限估计值越接近精确值。对应的速度图为图1-4-28b。

根据图1-4-28a的模式确定速度间断线的长度，根据图1-4-28b确定速度间断值，可得出虚拟功率方程为：

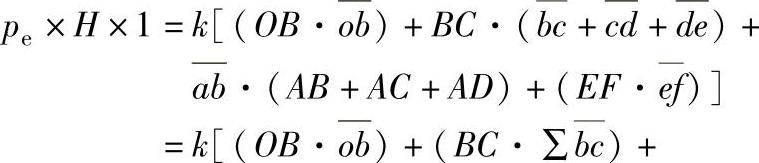
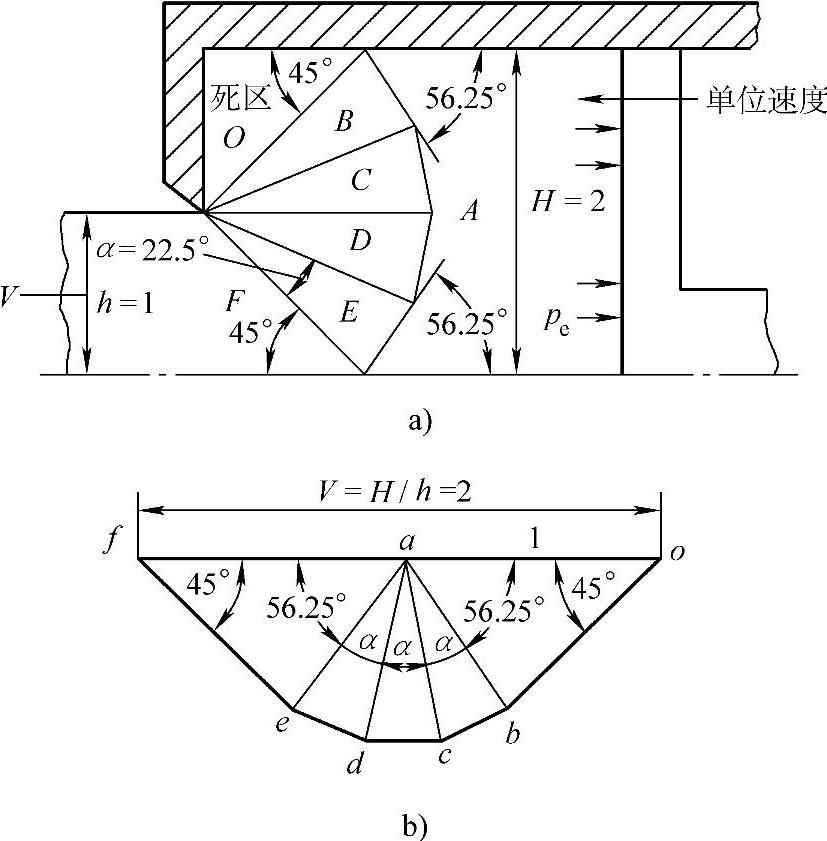
图1-4-28 断面收缩率为0.5的平面正挤压

a）刚性块上限模式 b）速度图

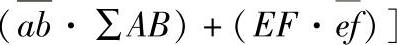
式中 p_e——凸模单位挤压力。

式中大写与小写字母分别代表速度间断线长度与速度间断值。

将相应的数值代入上式，可得到量纲为一的挤压力：

p_e/2k≈1.3

取极限状态，当刚性三角块的数目趋于无限多时，则边界形成一圆弧。于是，上限模式就成为如图1-4-28a所示的90°扇形刚性块，对应的速度图见图1-4-28b。

采用这样的模式得到的量纲为一的单位压力为：

p_e/2k≈1.29

这一结果和该问题的滑移线解是一致的。在参考文献[14]中Avitzur给出了楔形模平面挤压等问题的求解实例，此处不再赘述。