使用切块法解析变形力

切块法（slab method）是一种比较简单的分析接触面上正应力分布并计算平均变形抗力的计算方法。由于所推导的公式能表示出各因素（如摩擦、工件尺寸比、受力状态等）对平均变形抗力的影响，所以至今仍是计算变形力的重要方法之一。该方法的要点可归纳如下：

1）根据实际变形情况，将问题近似地按轴对称或平面问题处理。对于非稳定变形过程（如模锻），可以分阶段进行分析。

2）根据某瞬时的变形趋向，从变形体上截取包括接触面在内的典型基元块，且认为仅在接触面上有正应力和切应力（摩擦力），而在其余截面上仅有均布的正应力（即主应力）。在列平衡方程时，只按实际所受拉、压应力标明方向，不另考虑正负号，即以绝对值代入。

3）在应用屈服条件σ_max-σ_min=βR_eL时，忽略摩擦的影响，将接触面上正应力视为主应力。这时需考虑正负号，拉为正、压为负。根据变形趋势由应力应变顺序对应规律选定σ_max及σ_min的方位。

由图1-4-18所切取的基元块可见，其中都有一方向的尺寸是变形区的总尺寸而不是微小增量。即认为应力不随该方向的坐标变化，加之前已说明将实际问题归结为轴对称或平面应变问题，则应力平衡方程由偏微分方程变成常微分方程，求解比较方便。

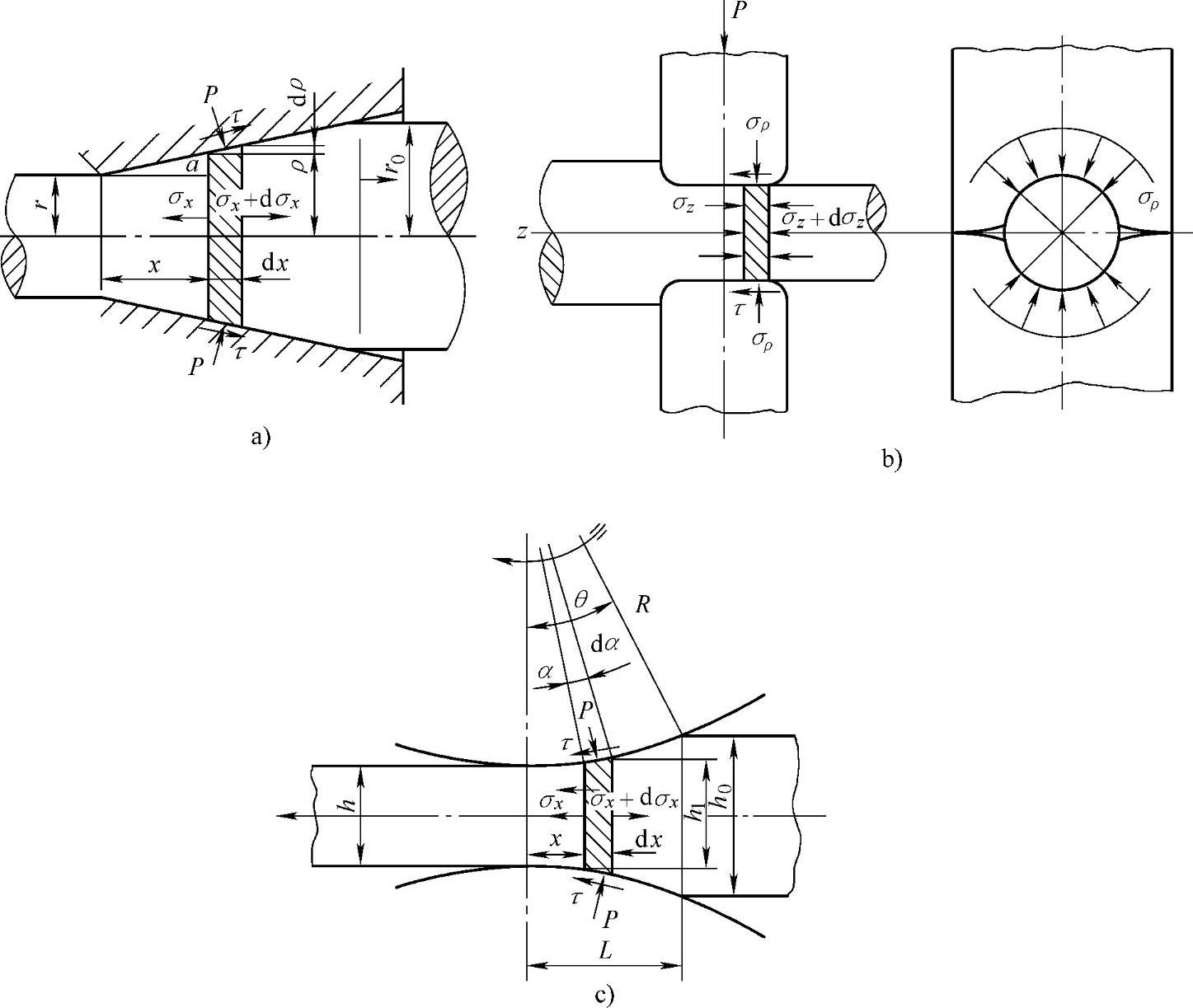
图1-4-18 切块法切取的基元块图例

a）拉拔 b）半圆模拉拔 c）轧制

现以圆柱体镦粗为例具体说明解题步骤。平行模板间圆柱体锻粗是典型的轴对称问题。解题主要步骤如下。

1.切取基元体

考虑到金属沿径向流动，切取如图1-4-19所示的基元体，高度为坯料瞬时高度h，厚度为dρ，圆心角为dθ，其上作用有应力σ_z、σ_ρ、σ_θ及τ。

2.列平衡方程

沿ρ向可列出平衡方程：

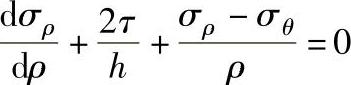
3.导出σ_ρ与σ_θ的关系

对于实心体圆柱体镦粗，径向应变增量dερ=dρ/ρ，而切向应变增量为：

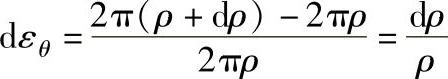
两式相等，根据应力应变关系理论将有：

σ_ρ=σ_θ

再将上式代入平衡方程可得：

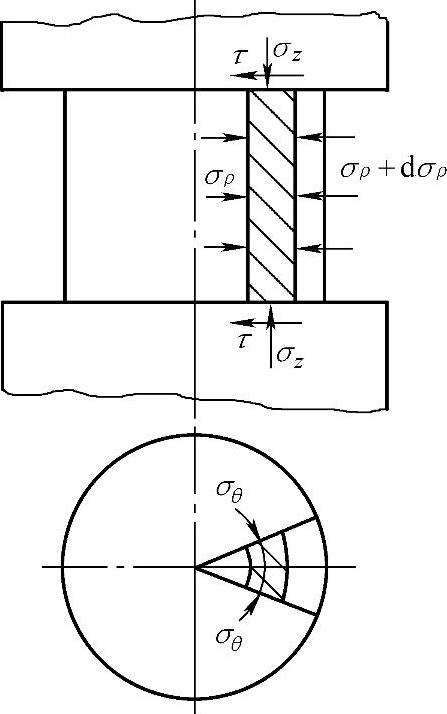
图1-4-19 切块法分析圆柱体镦粗应力示意图

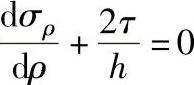
4.代入边界摩擦条件

设边界上τ取最大值，即：(www.xing528.com)

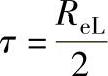
将此式代入上式，可得：

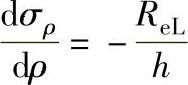
若设边界上τ=μσ_z，则又可得：

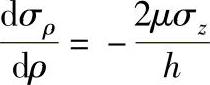
5.写出屈服准则的表达式

由应变状态可见，ε_ρ=ε_θ＞0，ε_z＜0。根据应力应变顺序对应规律（且考虑到应力的符号），可知（-σ_ρ）=（-σ_θ）=σ_max，（-σ_z）=σ_min，屈服准则为σ_max-σ_min=R_eL，将有摩擦力作用面上的正应力视为主应力，将有：

-σ_ρ+σ_z=R_eL

当认为接触面上摩擦力为极大值（τ_max=R_eL/2）时：

σ_z-σ_ρ=0

从上述两式都可得到：

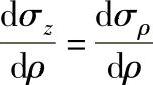
由此可见只要τ=常数，上式总是成立的，对于其余情况则是近似的。

将屈服条件与微分方程联立求解并确定积分常数，则可得到接触面上压力分布。

图1-4-20 镦粗单位压力分布

a）τ=R_eL/2 b）τ=μσ_z

6.不同摩擦条件下接触面上的压力分布公式

若设边界摩擦条件为τ=μR_eL，则接触面正应力分布公式为：

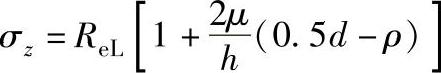
若设τ=μσ_z，则接触面正应力分布公式为：

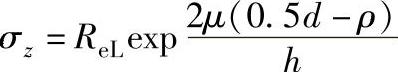
由以上解析可见，边界条件对接触面正压力分布影响很大，图1-4-20表示不同条件下接触面上正压力分布情况。