金属材料屈服准则及应用控制分析

对于金属材料而言，常用的有两个屈服准则，即最大切应力屈服准则和能量屈服准则。最大切应力准则认为：当一点的最大切应力值达到流动应力值之半时，该点即进入塑性状态。其表达式为τ_max=R_eL/2。当σ₁＞σ₂＞σ₃时该准则也可用式（1-4-26）表达：

σ₁-σ3=R_eL （1-4-26）

该准则是1864年由屈雷斯加（Tresca）首先提出，故又称屈雷斯加准则。其特点为只考虑最大及最小主应力而不考虑中间主应力的影响。在主应力空间中它的图形为与三坐标轴等倾斜的六棱柱面，又称屈雷斯加六棱柱面。柱面内为弹性状态，柱面上为塑性状态。

能量屈服准则认为当受力物体内一点处的形状改变弹性比能（单位体积的形状变化弹性位能）达到某一定值时，该点处即由弹性状态过渡到塑性状态。这个准则是1913年由米塞斯（Mises）首先提出，故又称Mises准则。它的表达式为：

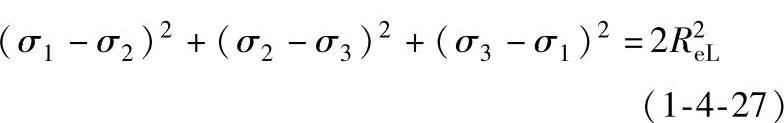
在主应力空间中，该式代表了一个无限长的圆柱面。柱面的半径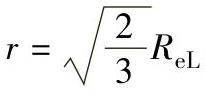，轴线通过原点并与坐标轴等倾斜（即与每个坐标轴夹角的方向余弦为）。这一圆柱面称为米塞斯圆柱面，面内为弹性状态，面上为塑性状态，亦称米塞斯屈服曲面。

图1-4-13为米塞斯圆柱面及屈雷斯加内接六棱柱面。过原点与圆柱轴线垂直的平面称π平面。不同的塑性变形工序在屈服面上占据不同的位置。

图1-4-13 米塞斯圆柱面与屈雷斯加六棱柱面

Mises屈服准则的物理意义于1924年由亨盖（Hencky）指出，它是用单位体积形状变化能的数值作为塑性变形是否发生的判据。

罗德于1926年通过研究铜、铁、镍等薄壁管在轴向拉力P和内部液压p的共同作用下的变形，验证了上述两屈服准则的正确性及相互关系。分析前提是假设主应力方向固定不变，应力顺序确定。当假设σ₁≥σ₂≥σ₃时，屈雷斯加屈服准则可写为：

通过分析得知，两个准则的主要区别在于是否考虑中间主应力σ₂的影响，为此他引入了参数μ，表示为：

该参数称为罗德参数，此时米塞斯屈服准则可以写成如下形式：

式中R_eL——流动应力。(www.xing528.com)

比较式（1-4-28）及式（1-4-30）可见，两者差别不大。最大为2/3（即1.155）。实验证明上述两准则是相差不大的，但米塞斯准则与实验结果更接近。

对于各向同性且等向强化的情况，可以将前述屈服准则由进入塑性状态推广到塑性变形继续进行的情况。此时，仅需将流动应力σ_s看成是与相应的应变速率、应变量相对应的真实应力即可。

变形过程中，工件各部位所处的应力状态，先满足屈服准则处先变形，后满足屈服准则处后变形，不满足屈服准则处不变形。例如，管材闭式镦粗（见图1-4-14）口部增厚快，底部可能未变形。原因是凹模侧壁摩擦力阻碍主作用力向下传播，沿高度上各截面受力是不等的。正确地利用屈服准则，可以控制变形在需要的部位发生。锻造时，工件中的不同部位的应力状态有较大的差异，而且同一点在不同的变形阶段其应力状态也不相同，因而各点在主应力空间中都有独立的加载轨迹，对于圆柱形坯料的镦粗，鼓肚表面处的平均应力代数值最大，并且一开始变形就出现了环向拉应力，这是该处易出现纵向裂纹的主要原因。

图1-4-14 管材闭式镦粗

在前面曾给出等效应力σ_i的表达形式，即：

因此，Mises屈服准则可以写成等效应力σ_i的表达形式，即：

Mises所给出的屈服准则也可用应力偏量第二不变量J₂来解释，即当J₂达到一定数值时，材料发生屈服，用公式表示为：

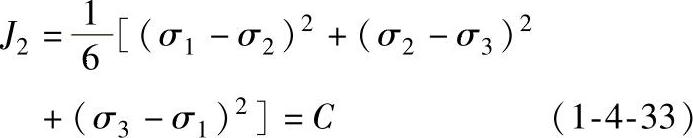
Eichinger和Nadai分别于1926年和1937年给出了米塞斯屈服准则的八面体切应力的表达，认为当八面体上切应力τ₈达到一定数值时材料发生屈服，即：

当然，米塞斯屈服准则还有其他多种表达形式及对应的物理解释，如应力圆总面积、主切应力平方和等，但是上述表达式中的变量表达式是完全相同的，只存在系数的差别。因此，这些表达式只是从不同侧面给出了米塞斯屈服准则的物理意义，在实际使用时是等效的。