三维图形展示应力分量

1.正应力三维图形

正应力沿着斜面的法线方向，其大小通常随着斜面的变化而变化。这种变化可以用式（1-4-7）来描述，也可以用三维图形更为形象地描述。

对于给定的σ₁，σ₂，σ₃，假设某斜面的法向的方向余弦为l，m，n，由式（1-4-7）可计算出该斜面上的正应力σ。沿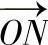方向作一模长等于|σ|的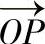矢量，则矢量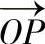的模就可以代表该作用面上的正应力的绝对值大小。变化l，m，n的数值，将得到不同方向上的正应力对应的矢量。连接各矢量的顶点，即可得到应力空间中一点的正应力三维图形。图1-4-8给出了典型的正应力三维图形，图中用深色和浅色分别表示正应力的正负。

和应力椭球面一样，从图1-4-8可以方便地得到不同斜面上正应力分量的变化，图形与三个主坐标轴的截距分别等于三个主应力的绝对值，而图形的形状和大小将随着主应力的变化而变化，即当三个主应力同时增加或减小一个数值时（改变静水应力分量），正应力三维图形将发生明显变化。对于金属材料，一般假设其变形与静水压力无关，因此上述图形不能反映应力状态与变形之间的本质联系。

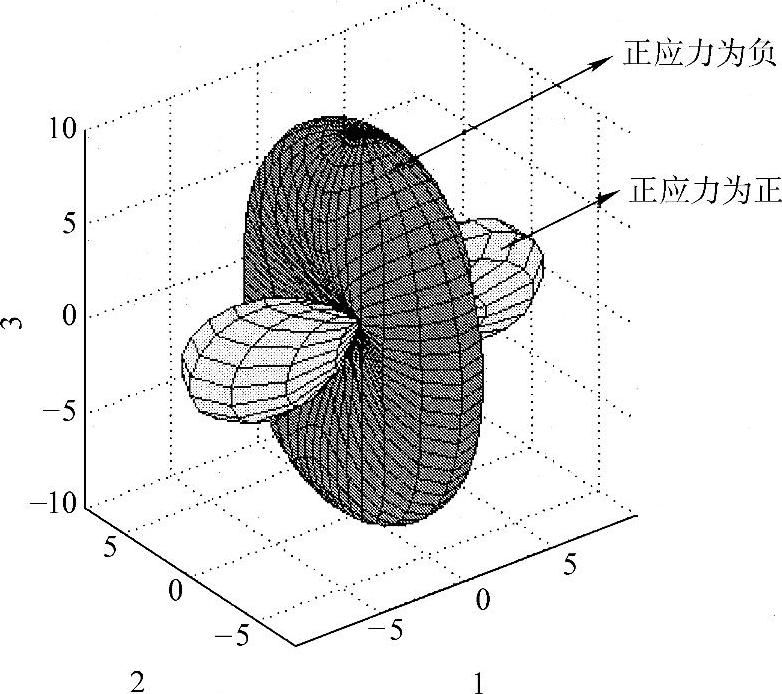
图1-4-8 典型正应力三维图形

图1-4-9中给出了三个不同应力状态去除静水应力分量后由应力偏量得到的正应力三维图形。经分析可知，应力偏量对应的正应力三维图形与应变类型有一一对应关系，从图形上颜色的不同还可以得出不同方向上的尺寸变化趋势，具体可以见参考文献[7，8]。

2.切应力三维图形

类似于正应力，也可以用三维图形来描述不同斜面上切应力的变化。图1-4-10给出了典型应力状态对应的切应力三维图形。

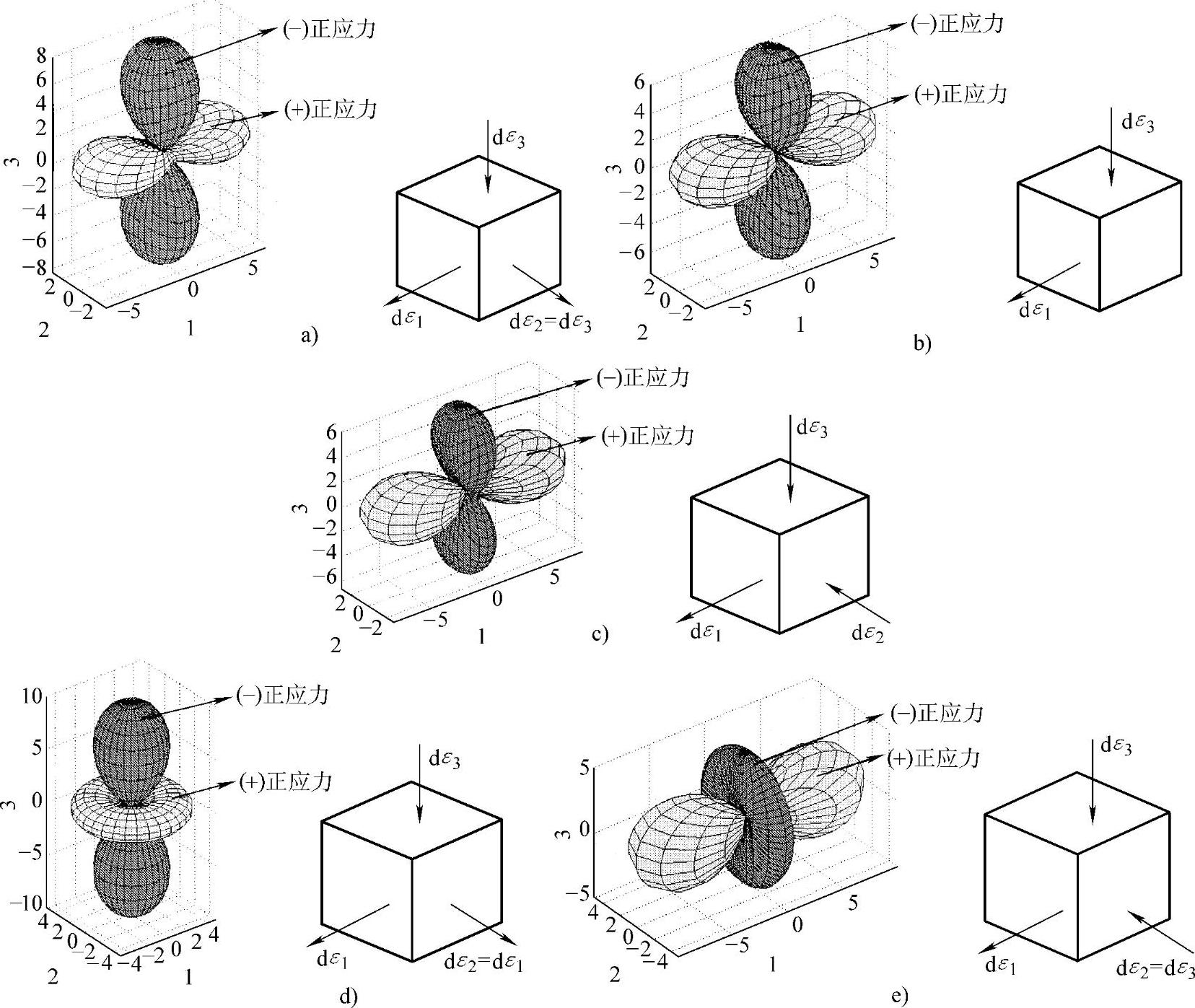
图1-4-9 典型应力偏量正应力三维图形及应变增量图形(www.xing528.com)

a）（10，8，4） b）（10，0，-10） c）（10，8，7） d）（10，10，-10） e）（10，-10，-10）

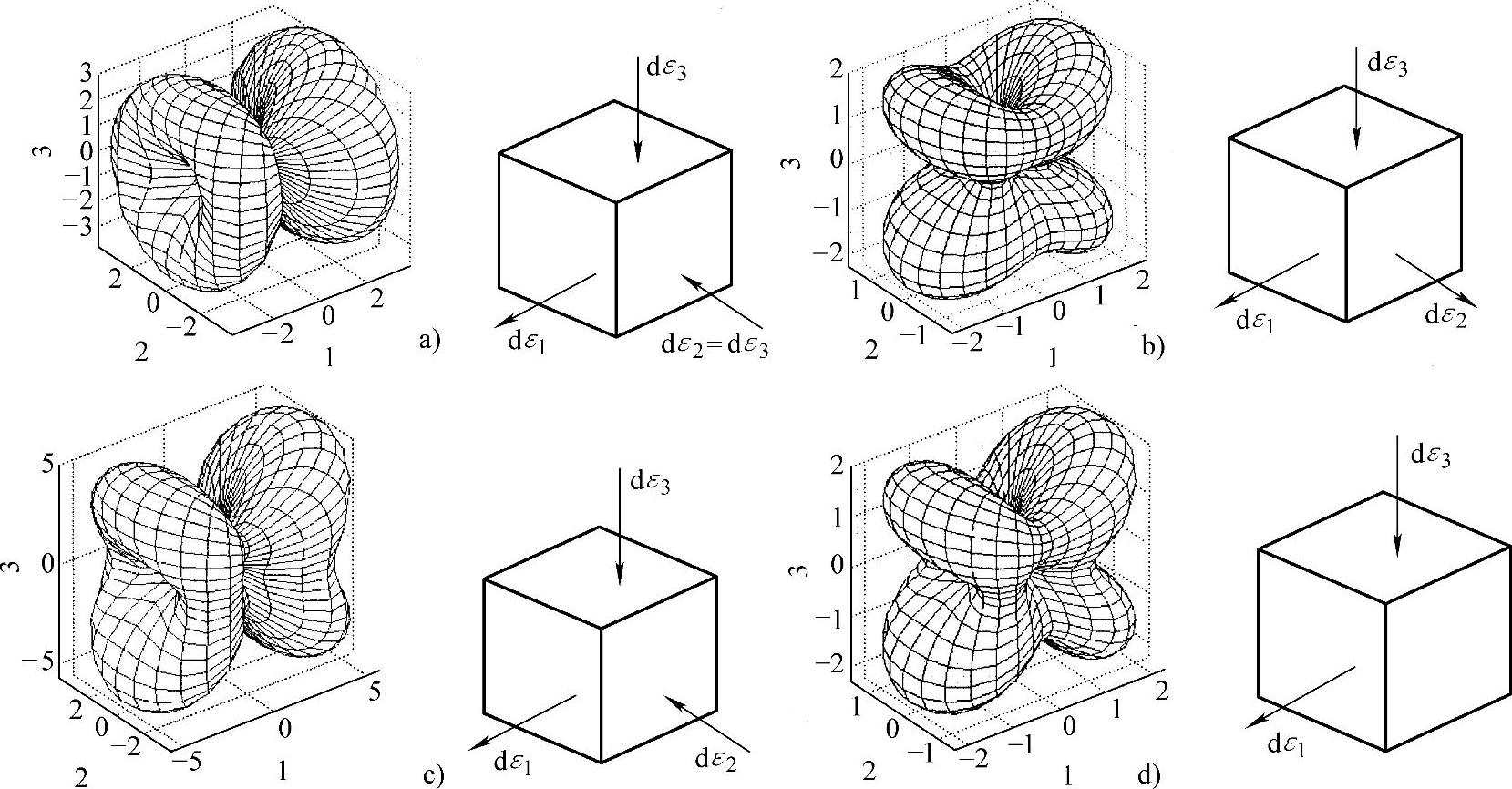
图1-4-10 典型应力偏量切应力三维图形及应变增量图形

a）（10，0，0） b）（10，8，4） c）（10，0，-5） d）（-4，-7，10）

从式（1-4-8）可以看出，切应力与三个主应力的相对差值或者说三个主偏应力分量σ′₁、σ′₂、σ′₃有关，而和平均应力σ_m无关，所以，某一应力状态及其偏应力状态对应的切应力图形形状相同。同样地，切应力三维图形与应变类型也有一一对应关系，从切应力三维图形的形状可以直观判断一点应力状态对应的应变情况。具体可见参考文献[9]。

3.全应力三维图形

如前所述，全应力的变化范围可以用应力椭球面来描述。但是，由于切应力分量的存在，全应力的作用方向一般并不沿着斜面的法线方向，因此从应力椭球面上并不能直接得到某一斜面上全应力的方向和大小。为此，采用类似方法可给出全应力三维图形。图1-4-11表示三向应力、平面应力及单向应力状态所对应的全应力图形。从坐标原点到三维图形上一点形成的矢量的模长可以表示以该矢量方向为法线方向的斜面上的全应力大小。全应力的真实作用方向可以通过公式计算得到。具体可见参考文献[10]。

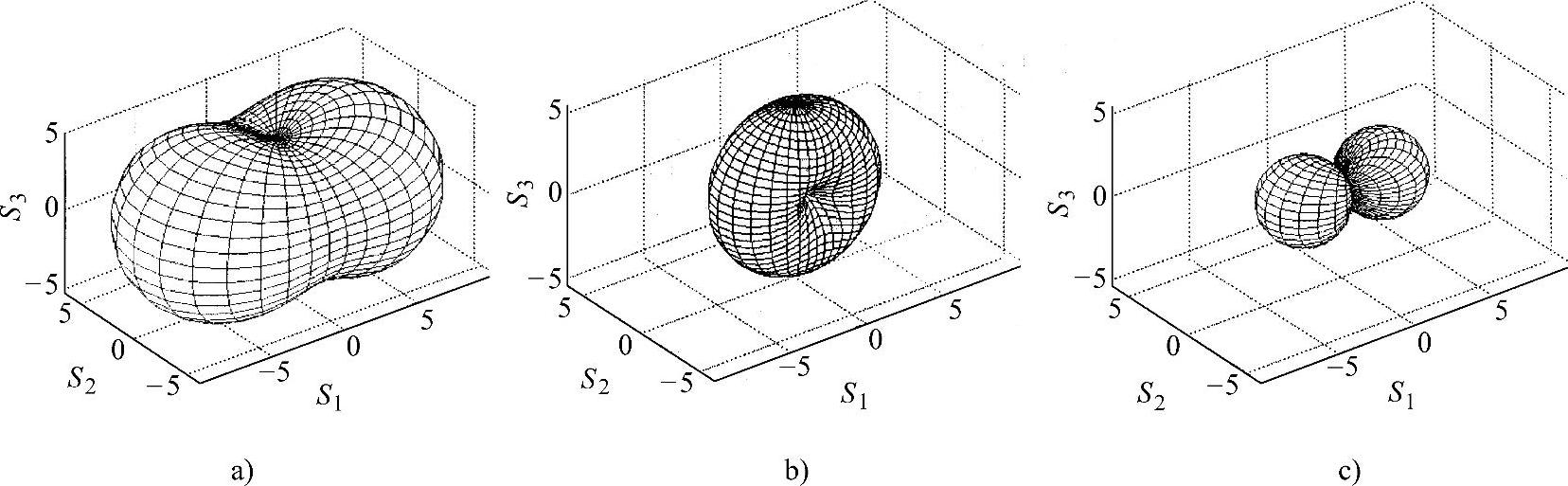
图1-4-11 典型应力状态的全应力三维图形

a）（10，6，4） b）（5，0，-5） c）（5，0，0）