应力分析中的应力莫尔圆和应力椭球面

对于应力空间中的一点，在过该点的不同平面上作用有不同的全应力。全应力又可以分解为互相垂直的正应力和切应力。设三维主应力空间中的一点为σ₁，σ₂，σ₃。过该点的某斜面上的全应力S、正应力σ和切应力τ如图1-4-1中所示。

正应力垂直于斜面，即沿着斜面的法线方向，切应力位于斜面内与正应力互相垂直，全应力为正应力和切应力分量的合成。

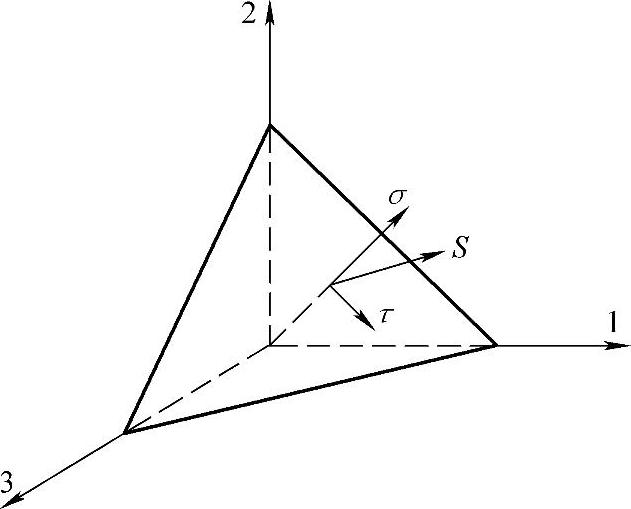
图1-4-1 主坐标系中任一斜面上的应力

在主坐标系中，设斜面法向的方向余弦为l，m，n，则该斜面上的S、σ和τ可分别表示为：

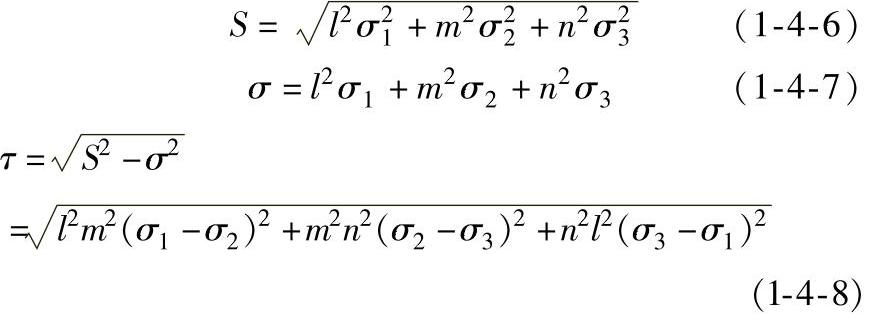
1.应力莫尔圆

莫尔圆是1882年Mohr为表示三向应力状态下过一点不同斜面上的正应力和切应力而提出的，它以图形方式描述了一点的应力状态或过一点不同斜面上正应力、切应力的变化。图1-4-2和图1-4-3分别为平面应力及三向应力状态对应的应力莫尔圆。在σ-τ坐标系中，应力莫尔圆给出了过单元体任一斜截面上的正应力与切应力的变化范围。图1-4-2中圆周上的一点、图1-4-3中三个圆周上及其所围阴影内一点的坐标代表单元体某一斜面上的正应力σ和切应力τ。根据应力莫尔圆，通过图解方法可以确定某一斜面上正应力和切应力的数值。

三向应力莫尔圆的构成可以由公式推导得出，其也可以理解为三个平面应力莫尔圆经过旋转合成而得，如图1-4-4和图1-4-5所示。具体可见参考文献[6]。

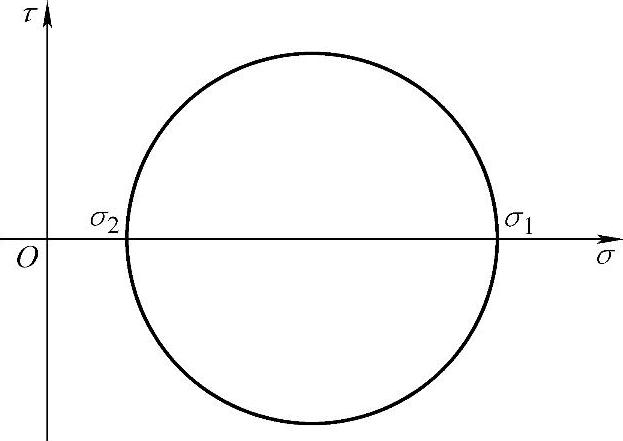
图1-4-2 平面应力莫尔圆

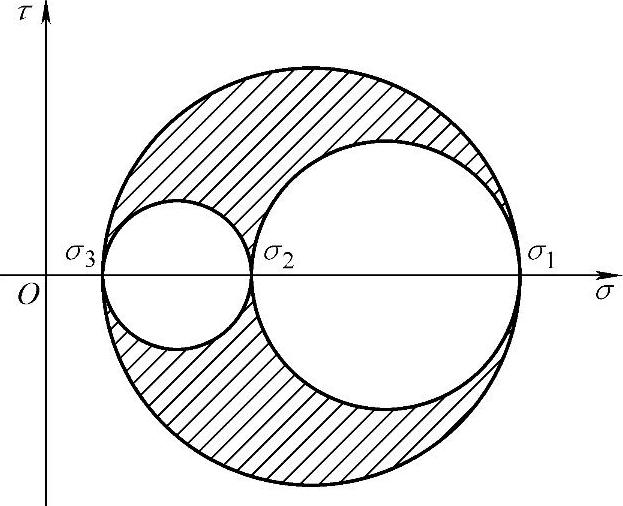
图1-4-3 三向应力莫尔圆

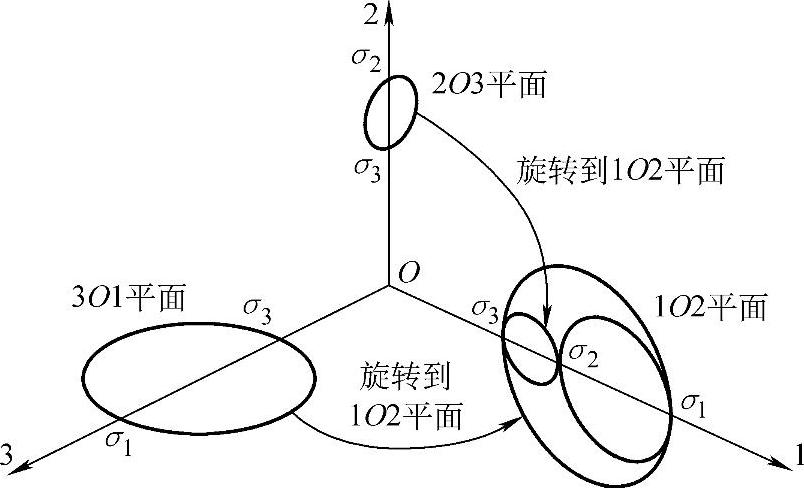
图1-4-4 三组平面应力莫尔圆

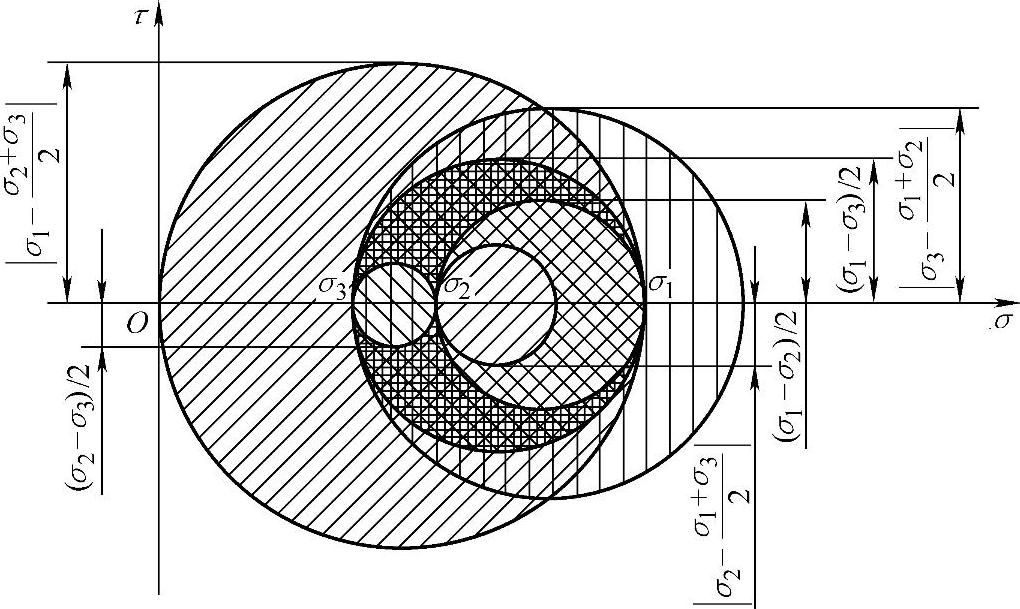
图1-4-5 由平面应力莫尔圆叠加成的三向应力莫尔圆(www.xing528.com)

当然，利用式（1-4-7）和式（1-4-8），通过变换方向余弦也可以直接计算得出可能的正应力、切应力组合。图1-4-6所示为变化方向余弦l（从-1～1）得到的所有可能的正应力和切应力组合，即如图1-4-3所示的三向应力莫尔圆。图中只给出了莫尔圆的上半部分。变化方向余弦m，n可以得到同样的结果。

塑性变形时，应力莫尔圆的直径受到屈服准则的限制。例如，按屈雷斯加准则，大圆直径为一常数，等于R_eL；而按米塞斯准则，大圆直径在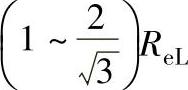范围内变化，但其圆心在横轴的位置是变化的，取决于平均应力σ_m的数值。

2.应力椭球面

对于过一点不同斜面上的全应力，其变化可以用应力椭球面来描述。对于主坐标系，三个坐标面上只作用有正应力而无切应力，此时全应力沿主轴方向的分量可表示为：

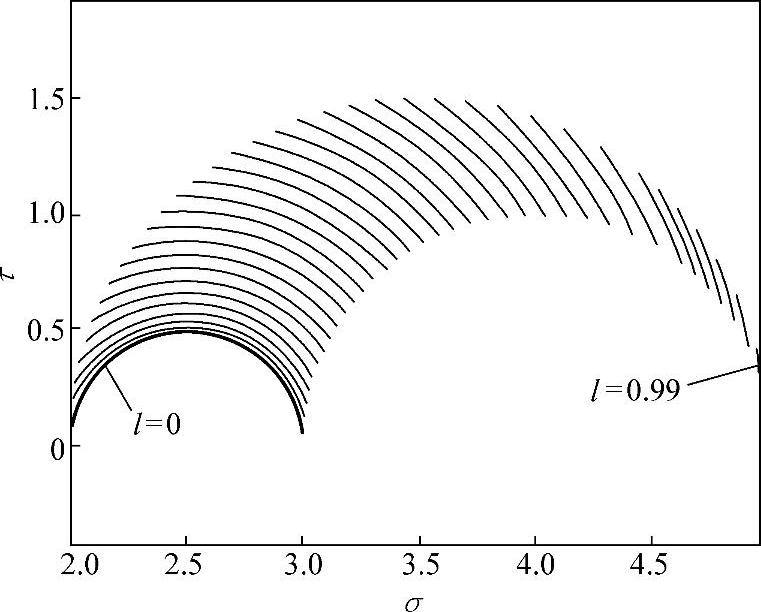
图1-4-6 不同的l对应的正应力和切应力

由上式可得：

因为l²+m²+n²=1，则由上式可得到：

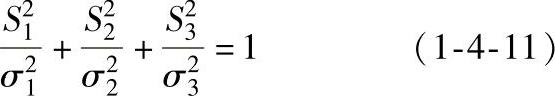
上式描述的即为如图1-4-7所示的应力椭球面。

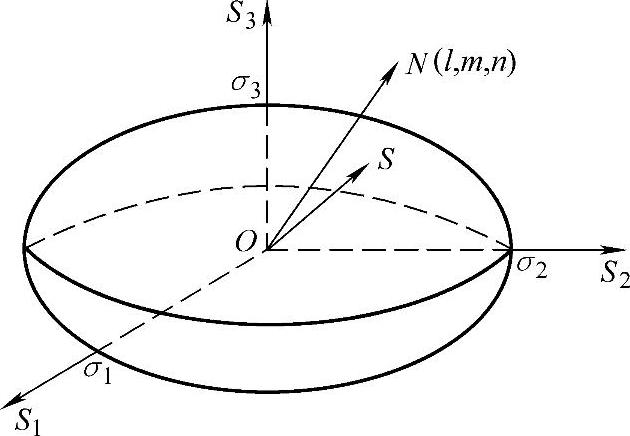
图1-4-7 应力椭球面

从坐标原点出发到应力椭球面上一点所形成的矢量，可以表示某一个斜面上的全应力分量。整个应力椭球面则可以描述过一点不同斜面上全应力的可能变化范围。

如果三个主应力有两个主应力的绝对值相等，则应力椭球面变为旋转椭球面，第三个主方向为旋转轴；如果三个主应力的绝对值互等，则应力椭球面变为球面。如果三个主应力中有一个主应力为零，则应力椭球面变为圆周；如果有两个主应力为零，则应力椭球面退化为一直线段。