例5-9 如图5-29所示,判断下列由集成模拟乘法器与集成运放构成的电路可以实现何种功能?
解 1)图5-29a所示电路中uX=uY=ui,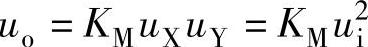 ,输出信号uo与输入信号ui的二次方成正比,所以该电路可以实现平方运算功能。
,输出信号uo与输入信号ui的二次方成正比,所以该电路可以实现平方运算功能。
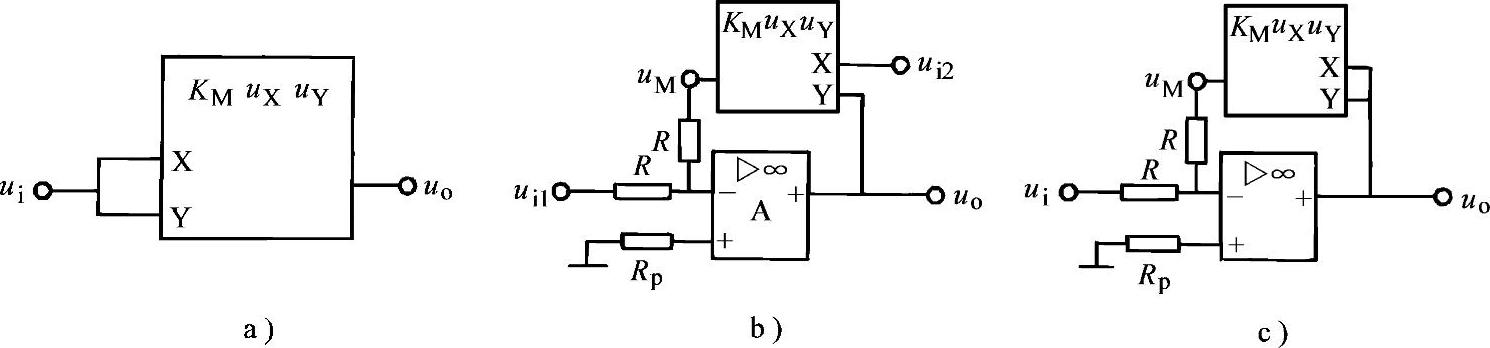
图5-29 例5-9
2)图5-29b所示电路中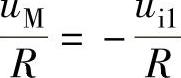 ,即uM=-ui1,且uM=KMui2uo,于是
,即uM=-ui1,且uM=KMui2uo,于是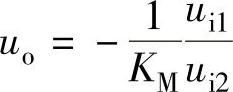 。输出信号uo与两个输入信号ui1、ui2的商成正比,所以该电路可以实现除法运算功能。
。输出信号uo与两个输入信号ui1、ui2的商成正比,所以该电路可以实现除法运算功能。
为了保持电路稳定,电路应为负反馈,所以必须使ui2>0,这样才能保持uo↑→uM↑→uo↓,而ui1可正可负。否则电路将自行锁闭(即当ui2<0时,有uo↑→uM↓→uo↑,正反馈),无法实现除法运算。
如果要想在ui2<0时实现除法运算,应加一反相器将ui2反相后再加入模拟乘法器。
3)图5-29c所示电路中uM=KMu2o=-ui,则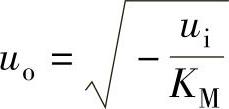 ,输出信号uo与输入信号ui的平方根成反比,所以该电路可以实现开方运算功能。
,输出信号uo与输入信号ui的平方根成反比,所以该电路可以实现开方运算功能。
由于KM>0,所以ui<0时可以实现开方运算。如果要想在ui>0时实现开方运算,应加一反相器将ui反相后再加入模拟乘法器。
例5-10 如图5-30所示电路,设KM=0.1V-1,直流电压US=10V,高频信号uc(t)=4cosωct,低频信号uΩ(t)=5cosωΩt,其中ωc>>ωΩ。试求各电路的输出电压uo,并画出图b和图c电路中uΩ、uc、uo的振幅频谱图。
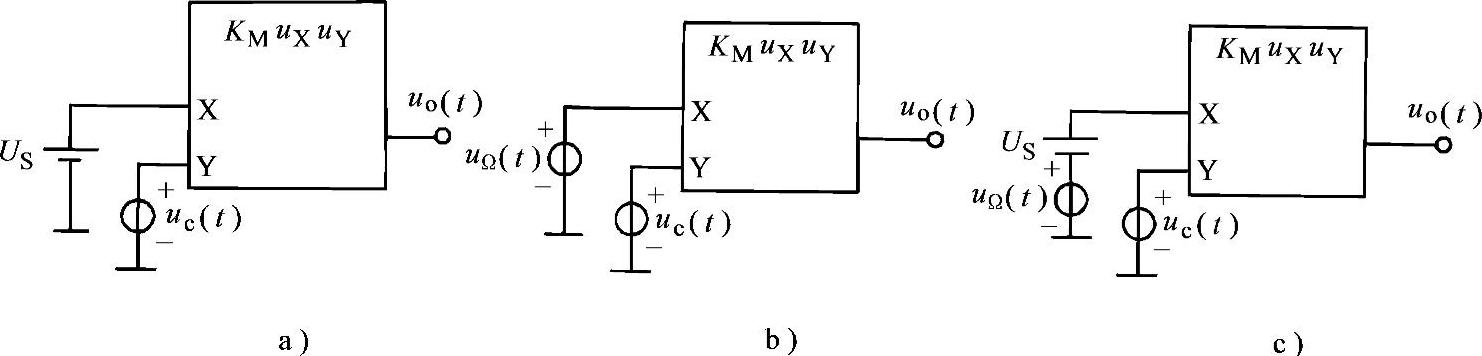
图5-30 例5-10
解 1)图5-30a所示电路中uo=KMUSuc(t)=4cosωct。
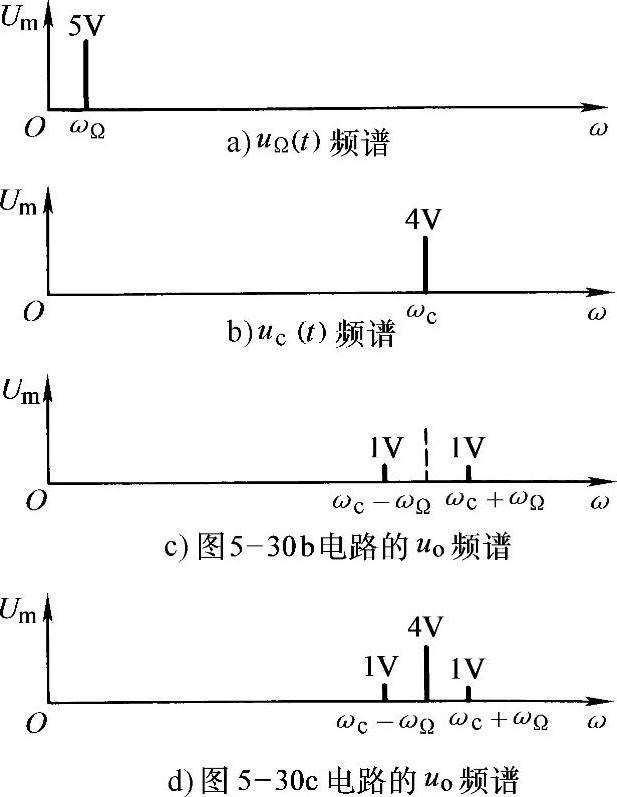
2)图5-30b所示电路中uo=KMuΩ(t)uc(t)=2cosωΩtcosωct=cos(ωc+ωΩ)t+cos(ωc-ωΩ)t,频谱图如图5-31所示。
3)图5-30c所示电路中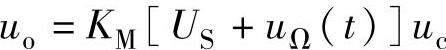
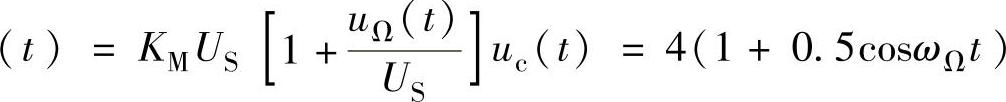 cosωct=4cosωct+2cosωΩtcosωct=4cosωct+cos(ωc+ωΩ)t+cos(ωc-ωΩ)t,频谱图如图5-31所示。在例5-10中,图5-30a电路实际是一压控增益放大器,电压增益为Au=uo/uc=KMUS,显然调整直流电压US可以控制增益Au的大小;图5-30b电路是一双边带调幅电路,图5-30c电路是普通调幅(AM)电路,由频谱图可以看出,调幅过程的实质是将低频(调制信号)频谱“搬移”到高频(载波信号)频谱的两侧。可见使用模拟乘法器可以实现频率变换(频谱交换)。
cosωct=4cosωct+2cosωΩtcosωct=4cosωct+cos(ωc+ωΩ)t+cos(ωc-ωΩ)t,频谱图如图5-31所示。在例5-10中,图5-30a电路实际是一压控增益放大器,电压增益为Au=uo/uc=KMUS,显然调整直流电压US可以控制增益Au的大小;图5-30b电路是一双边带调幅电路,图5-30c电路是普通调幅(AM)电路,由频谱图可以看出,调幅过程的实质是将低频(调制信号)频谱“搬移”到高频(载波信号)频谱的两侧。可见使用模拟乘法器可以实现频率变换(频谱交换)。
 (https://www.xing528.com)
(https://www.xing528.com)
图5-31 例5-10的频谱图
例5-11 由模拟乘法器与低通滤波器构成的正弦鉴相器电路如图5-32所示,设uX=UXmsin(ωt+φ),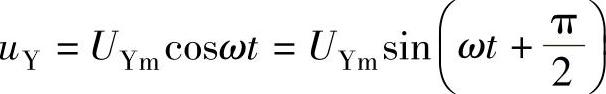 ,即设定uX的初相位φ以uY的初相位
,即设定uX的初相位φ以uY的初相位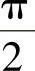 (即90°)作为相位参考点。1)证明:uo=Uomsinφ,其中
(即90°)作为相位参考点。1)证明:uo=Uomsinφ,其中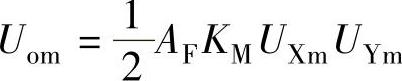 ,AF为低通滤波器通带的电压传输系数。2)画出鉴相特性曲线uo-φ。3)当uo=0、Uom、-Uom、
,AF为低通滤波器通带的电压传输系数。2)画出鉴相特性曲线uo-φ。3)当uo=0、Uom、-Uom、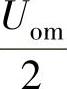 、
、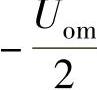 时,uX与uY的相位差Δφ各是多少(在-π≤φ≤π范围内计算)?
时,uX与uY的相位差Δφ各是多少(在-π≤φ≤π范围内计算)?
解 1)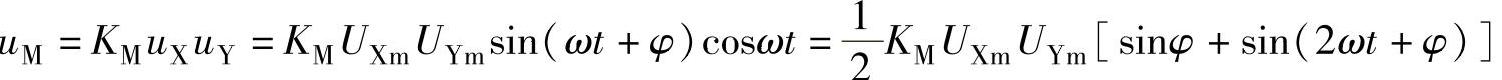 =U′omsinφ+U′omsin(2ωt+φ),其中
=U′omsinφ+U′omsin(2ωt+φ),其中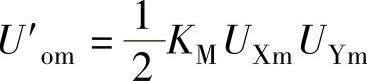 ,uM经过低通滤波器滤除高频交流分量U′omsin(2ωt+φ),可得到
,uM经过低通滤波器滤除高频交流分量U′omsin(2ωt+φ),可得到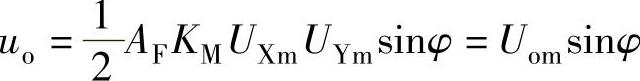 。
。
2)画出鉴相特性曲线uo-φ如图5-33所示。
3)当uo=0时,φ=0、±π,uX与uY的相位差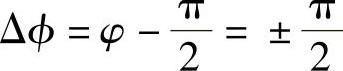 ,即uX与uY正交。
,即uX与uY正交。
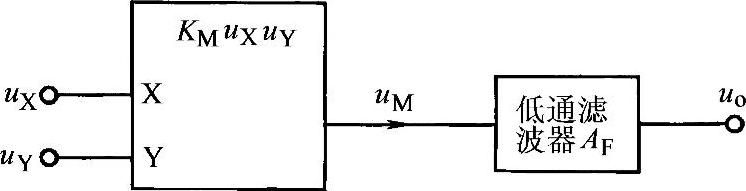
图5-32 正弦鉴相器
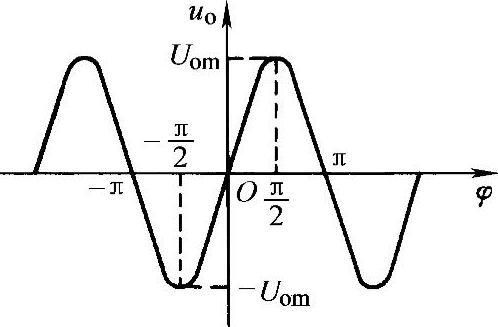
图5-33 正弦鉴相器的鉴相特性曲线
当uo=Uom时,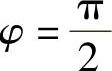 ,uX与uY的相位差
,uX与uY的相位差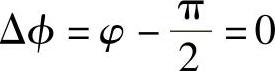 ,即uX与uY同相。
,即uX与uY同相。
当uo=-Uom时,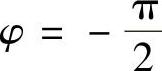 ,uX与uY的相位差
,uX与uY的相位差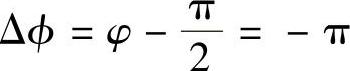 或π,即uX与uY反相。
或π,即uX与uY反相。
当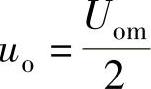 时,
时,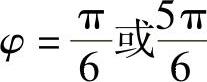 ,uX与uY的相位差
,uX与uY的相位差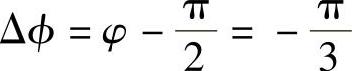 或
或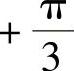 ,即uX与uY相位差大小为60°。
,即uX与uY相位差大小为60°。
当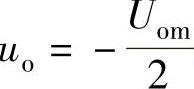 时,
时,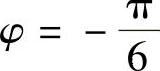 ,
,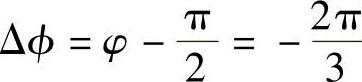 ;或
;或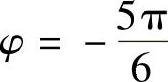 ,Δ
,Δ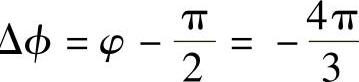 ,由于
,由于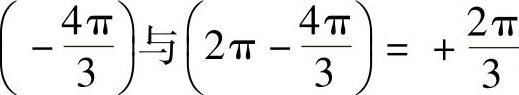 是相同的角,则
是相同的角,则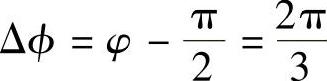 ,即uX与uY相位差大小为120°。
,即uX与uY相位差大小为120°。
例5-11表明鉴相器的输出电压uo的大小反映出两个输入信号uX与uY的相位差的大小,所以可以根据其输出电压uo的数值和正负号鉴别出两个输入信号uX与uY的相位差的大小。当0≤uo≤Uom时,uX与uY的相位差为0°~90°;当-Uom≤uo≤0时,uX与uY相位差为90°~180°。
应用模拟乘法器构成的实用电路相当繁多,本书不再一一赘述。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




